Решение. Разложим подынтегральную функцию в степенной ряд по формуле
Разложим подынтегральную функцию в степенной ряд по формуле
Полученный знакочередующийся ряд удовлетворяет условиям теоремы Лейбница. Так как четвёртый его член по абсолютной величине меньше 0, 001, то для обеспечения заданной точности достаточно взять первые три члена ряда. Получаем:
.
9. Разложить заданную функцию Решение. Так как по условию ряд должен содержать только синусы кратных углов, то следует продолжить заданную функцию на отрезок
Так как заданная функция нечетная, то коэффициенты ряда Фурье
и ряд Фурье имеет вид Подставляя заданную функцию, получаем
Последний интеграл вычисляем методом интегрирования по частям, полагая
Таким образом, искомое разложение имеет вид
или
10. Дана функция двух переменных 1) экстремум функции 2) 3) наибольшую скорость возрастания
Решение. 1) Для отыскания экстремума функции
Приравняем их к нулю и решим систему уравнений:
Решением системы является точка М (–4; 1). Точка М (–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точке М:
Из них составим определитель второго порядка
Так как 2) Градиент функции
Градиент функции
3) Наибольшая скорость возрастания функции равна модулю градиента:
11. Вычислить массу неоднородной пластинки треугольной формы с вершинами в точках О (0; 0), А (5; 0), В (0; 7), поверхностная плотность которой в точке М (х; у) равна
|

 Тогда
Тогда




 .
. в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке  .
. нечетным образом, затем продолжить на всю числовую ось с периодом
нечетным образом, затем продолжить на всю числовую ось с периодом  . Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида:
. Теперь разложим полученную периодическую функцию в ряд Фурье (эта операция разложения называется гармоническим анализом) вида: .
. , а
, а  вычисляем по формуле
вычисляем по формуле
 .
. .
. . Отсюда
. Отсюда 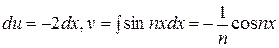 . следовательно,
. следовательно,



 . Найти:
. Найти: ;
; в точке А (1; –2);
в точке А (1; –2);



 , то в точке М (–4; 1) есть экстремум. Производная
, то в точке М (–4; 1) есть экстремум. Производная  , а, значит, это точка минимума функции.
, а, значит, это точка минимума функции.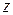 найдем по формуле:
найдем по формуле: ,
,  и
и  были найдены в пункте 1.
были найдены в пункте 1. .
. .
. .
. .
.


