1) Для того чтобы построить вариационный ряд, сначала находят 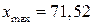 ,
,  и размах вариационного ряда
и размах вариационного ряда 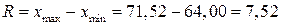 , затем определяют число интервалов
, затем определяют число интервалов  по формуле
по формуле  с округлением до ближайшего целого числа. В нашем случае
с округлением до ближайшего целого числа. В нашем случае 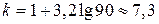 . Возьмём
. Возьмём  . Длина каждого интервала вычисляется по формуле
. Длина каждого интервала вычисляется по формуле  . Число
. Число  всегда округляют с избытком.
всегда округляют с избытком.
В рассматриваемом примере  Положим
Положим  .
.
Границы интервалов последовательно вычисляют по формулам 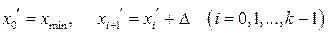 .
.
Для каждого i-го интервала подсчитывают количество 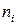 попавших в него данных
попавших в него данных  . Если выборочное данное совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером. Затем вычисляют относительные частоты
. Если выборочное данное совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером. Затем вычисляют относительные частоты 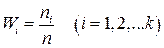 . Таким образом, получаем вариационный ряд (см. таблицу 2).
. Таким образом, получаем вариационный ряд (см. таблицу 2).
Таблица 2.
| №
интервала
| интервалы
| Частоты 
| 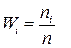
|
|
| (64, 00; 65, 08)
(65, 08; 66, 16)
(66, 16; 67, 24)
(67, 24; 68, 32)
(68, 32; 69, 40)
(69, 40; 70, 48)
(70, 48; 71, 56)
|      8 8
       11 11
       14 14
             20 20
           17 17
         16 16
 4 4
| 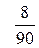
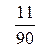


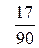
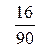
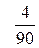
|
2) В качестве оценки математического ожидания (генеральной средней) берётся среднее арифметическое выборочных данных  .
.
За оценку дисперсии берётся исправленная выборочная дисперсия
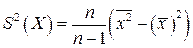 , где
, где 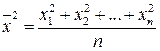 .
.
Этими формулами пользуются в случае небольшого объёма выборки (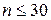 ). При выполнении расчётов при большом объёме выборки, то есть когда уже построен вариационный ряд
). При выполнении расчётов при большом объёме выборки, то есть когда уже построен вариационный ряд  вычисляется по формуле
вычисляется по формуле
 , (1)
, (1)
где  - середина i-го интервала. Исправленная дисперсия
- середина i-го интервала. Исправленная дисперсия 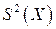 вычисляется по формуле
вычисляется по формуле 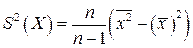 , где
, где
 . (2)
. (2)
Вычисления по формулам (1) и (2), как правило, сложны, поэтому для упрощения расчётов переходят от величин  к величинам
к величинам  по формуле
по формуле
 .
.
Величину  выберем следующим образом:
выберем следующим образом:
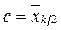 , если
, если  – четное,
– четное,
 , если
, если  – нечетное.
– нечетное.
При таком выборе формулы перехода величины  будут принимать последовательные целые значения, близкие к нулю (см. таблицу 3).
будут принимать последовательные целые значения, близкие к нулю (см. таблицу 3).
Таблица 3.

| 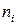
| 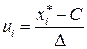
| 
| 
| 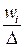
| 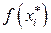
|
| 64, 540
65, 620
66, 700
67, 780
68, 860
69, 940
71, 020
|
| -3
-2
-1
| -24
-22
-14
|
| 0, 08
0, 11
0, 15
0, 20
0, 18
0, 17
0, 04
| 0, 04
0, 10
0, 18
0, 22
0, 19
0, 12
0, 05
|
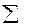
|
|
|
|
|
|
|
В нашем случае С= 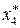 =67, 78, вычисляем
=67, 78, вычисляем  ,
,
 ,
, 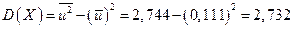 ; затем по формулам
; затем по формулам
 ,
,  ,
,
найдём 
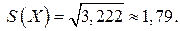
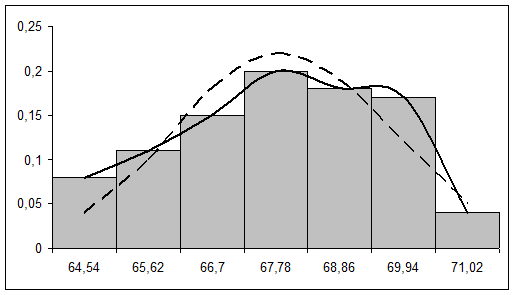
3) Гистограммой относительных частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиной  , расположенные на оси Ох, а высоты равны
, расположенные на оси Ох, а высоты равны  .
.
Соединив середины верхних сторон прямоугольников плавной линией, получим аналог плотности распределения случайной величины 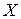 (график эмпирической плотности распределения).
(график эмпирической плотности распределения).
4) По виду кривой эмпирического распределения («колоколообразная» кривая) можно предположить, что случайная величина 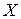 распределена по нормальному закону. Для сравнения в той же системе координат построим кривую плотности нормального распределения:
распределена по нормальному закону. Для сравнения в той же системе координат построим кривую плотности нормального распределения:
 , где
, где 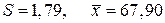
Мы использовали значения, полученные во втором пункте.
В случае нормального распределения величины 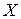 вероятность того, что отклонение
вероятность того, что отклонение  от
от  окажется больше, чем величина
окажется больше, чем величина  , должна быть очень мала, близка к нулю. Это означает, что практически почти все значения выборочных данных должны попасть в интервал
, должна быть очень мала, близка к нулю. Это означает, что практически почти все значения выборочных данных должны попасть в интервал 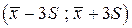 , в нашем случае - в интервал (62, 53; 73, 27).
, в нашем случае - в интервал (62, 53; 73, 27).
Так как в рассматриваемом примере все выборочные значения попадают в указанный интервал, то есть основание считать, что случайная величина 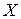 распределена по нормальному закону с плотностью вероятности
распределена по нормальному закону с плотностью вероятности  . Для сравнения построим график этой функции, предварительно вычислив значения этой функции в точках
. Для сравнения построим график этой функции, предварительно вычислив значения этой функции в точках  (см. последний столбец таблицы 3). Найдём также максимум этой функции:
(см. последний столбец таблицы 3). Найдём также максимум этой функции:  3.
3.

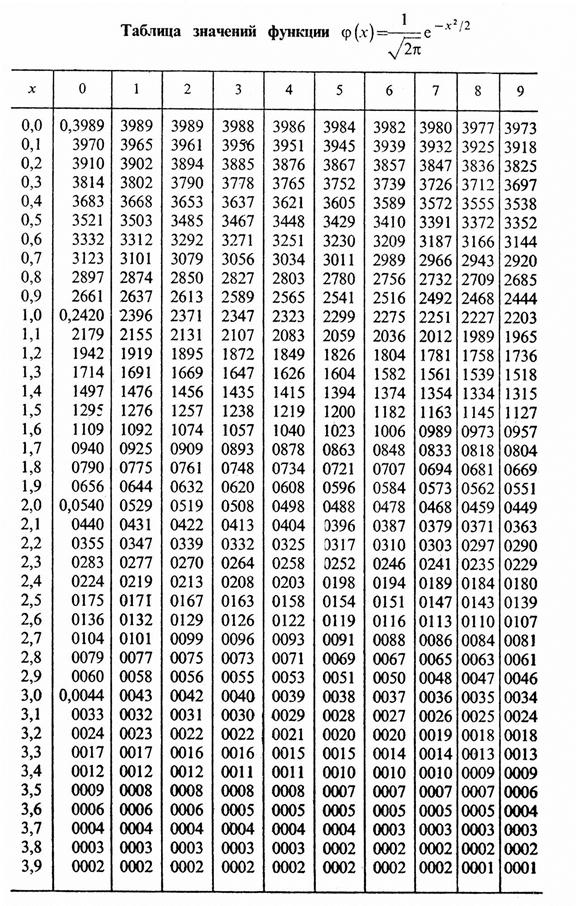
ПРИЛОЖЕНИЯ
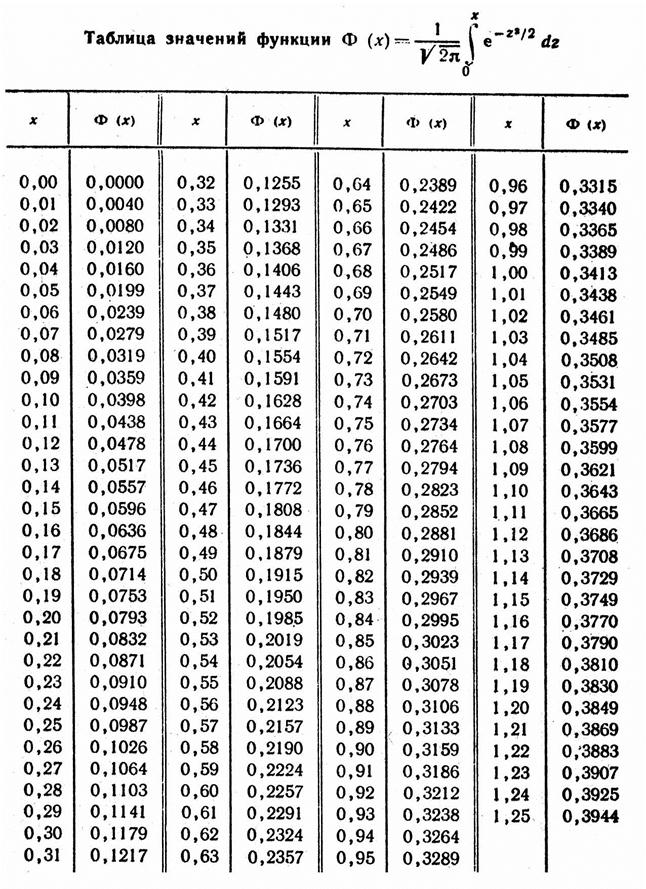
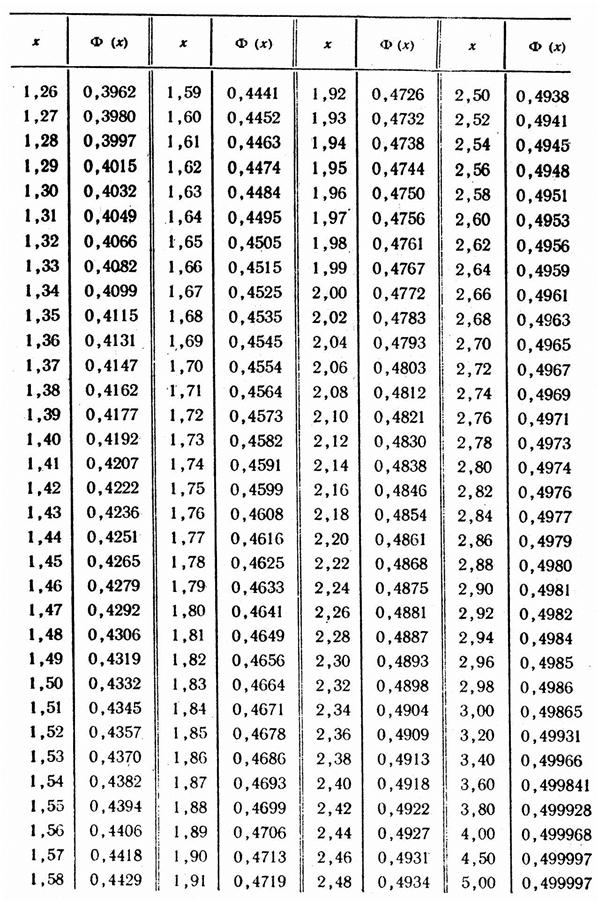
Продолжение таблицы значений функции Ф(х)
ОГЛАВЛЕНИЕ
| Таблицы вариантов………………………………………………………………
|
|
| Задания для контрольных работ. Контрольная работа №1…………………...
|
|
| Контрольная работа №2…………………………………………………………
|
|
| Решение типовых примеров. Контрольная работа №1….…………………….
|
|
| Решение типовых примеров. Контрольная работа №2….…………………….
|
|
| Приложения………………………………………………………………………
|
|

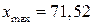 ,
,  и размах вариационного ряда
и размах вариационного ряда 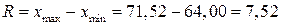 , затем определяют число интервалов
, затем определяют число интервалов  по формуле
по формуле  с округлением до ближайшего целого числа. В нашем случае
с округлением до ближайшего целого числа. В нашем случае 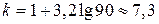 . Возьмём
. Возьмём  . Длина каждого интервала вычисляется по формуле
. Длина каждого интервала вычисляется по формуле  . Число
. Число  всегда округляют с избытком.
всегда округляют с избытком. Положим
Положим  .
.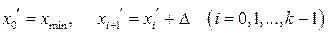 .
.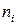 попавших в него данных
попавших в него данных  . Если выборочное данное совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером. Затем вычисляют относительные частоты
. Если выборочное данное совпадает с границей двух соседних интервалов, то его следует отнести к интервалу с меньшим номером. Затем вычисляют относительные частоты 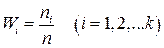 . Таким образом, получаем вариационный ряд (см. таблицу 2).
. Таким образом, получаем вариационный ряд (см. таблицу 2).
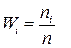




 8
8





 11
11






 14
14

















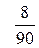
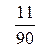


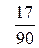
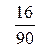
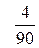
 .
.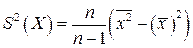 , где
, где 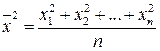 .
.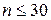 ). При выполнении расчётов при большом объёме выборки, то есть когда уже построен вариационный ряд
). При выполнении расчётов при большом объёме выборки, то есть когда уже построен вариационный ряд  вычисляется по формуле
вычисляется по формуле , (1)
, (1) - середина i-го интервала. Исправленная дисперсия
- середина i-го интервала. Исправленная дисперсия 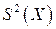 вычисляется по формуле
вычисляется по формуле  . (2)
. (2) к величинам
к величинам  по формуле
по формуле .
. выберем следующим образом:
выберем следующим образом: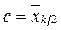 , если
, если  – четное,
– четное, , если
, если  будут принимать последовательные целые значения, близкие к нулю (см. таблицу 3).
будут принимать последовательные целые значения, близкие к нулю (см. таблицу 3).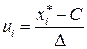


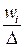
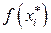
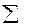
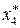 =67, 78, вычисляем
=67, 78, вычисляем  ,
, ,
, 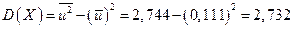 ; затем по формулам
; затем по формулам ,
,  ,
,
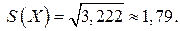
 .
. (график эмпирической плотности распределения).
(график эмпирической плотности распределения). , где
, где 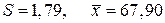
 , должна быть очень мала, близка к нулю. Это означает, что практически почти все значения выборочных данных должны попасть в интервал
, должна быть очень мала, близка к нулю. Это означает, что практически почти все значения выборочных данных должны попасть в интервал 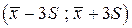 , в нашем случае - в интервал (62, 53; 73, 27).
, в нашем случае - в интервал (62, 53; 73, 27). . Для сравнения построим график этой функции, предварительно вычислив значения этой функции в точках
. Для сравнения построим график этой функции, предварительно вычислив значения этой функции в точках  3.
3.







