КОНТРОЛЬНАЯ РАБОТА №1. 1. Решить систему линейных уравнений методом Гаусса
1. Решить систему линейных уравнений методом Гаусса.
Решение. Первое уравнение умножается на (-2) и прибавляется ко второму уравнению, затем первое уравнение умножается на (-3) и прибавляется к третьему. Таким образом, неизвестное х исключается из двух последних уравнений. Эти преобразования лучше показать на расширенной матрице
Вычтя во второй матрице из третьей строки удвоенную вторую, мы исключаем неизвестное у из третьего уравнения. После таких преобразований получается система
Из третьего уравнение легко находится Нетрудно проверить, что совокупность
2. Определить тип кривой
Решение. Приведем уравнение кривой Уравнение прямой Угловой коэффициент Для нахождения точек пересечения этих линий решим систему
Возведем второе уравнение в квадрат
и подставим в первое уравнение:
Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.
–5 0 5 х
-3
3. Даны координаты вершин пирамиды АВСD:
1) записать векторы 2) найти угол между векторами 3) найти проекцию вектора 4) найти площадь грани АВС; 5) найти объем пирамиды АВСD; 6) составить уравнение ребра АС; 7) составить уравнение грани АВС.
|







 .
.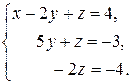
 . Затем из второго уравнения получаем
. Затем из второго уравнения получаем  . Наконец, из третьего уравнения получаем
. Наконец, из третьего уравнения получаем  .
. ,
,  , найти ее параметры; определить угловой коэффициент прямой
, найти ее параметры; определить угловой коэффициент прямой  . Найти точки пересечения данных линий и сделать чертеж.
. Найти точки пересечения данных линий и сделать чертеж. к каноническому виду
к каноническому виду  , разделив на 225. Получим уравнение эллипса
, разделив на 225. Получим уравнение эллипса 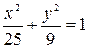 . Его большая полуось
. Его большая полуось 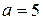 , малая полуось
, малая полуось  . Центр совпадает с началом координат.
. Центр совпадает с началом координат. , что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду
, что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду  , выразим у через х:
, выразим у через х:  .
. .
.

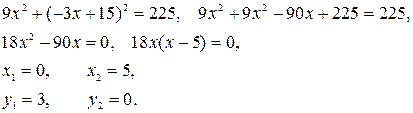
 у
у 



 Требуется:
Требуется: в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов; и
и  ;
; на вектор
на вектор  ;
;


