Решение. 1) Область определения функции
1) Область определения функции
2) Исследование на непрерывность и классификация точек разрыва. Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:
Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика. 3) Исследование на экстремум и промежутки монотонности.
4) Исследование графика на выпуклость, вогнутость, точки перегиба.
Так как
5) Исследование графика на наличие наклонных асимптот.
Таким образом, прямая 6) График заданной функции пересекает ось Оу в точке (0; –5). По результатам исследования строим график.
5. Решить систему двух линейных уравнений в области комплексных чисел по формулам Крамера. Найденные
Решение. Найдем решение системы линейных уравнений по формулам Крамера
Находим
Таким образом, решение данной системы уравнений в алгебраической форме записи:
в векторной форме записи
-2 0 3, 5
Найдем модуль Число
Число
Запишем числа
6. а) Вычислить площадь фигуры, расположенной в первом квадранте и ограниченной параболой б) Найти объем тела, образованного вращением этой фигуры вокруг оси Ох.
|

 .
.






 .
.
 , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:
, то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:








 – наклонная асимптота графика.
– наклонная асимптота графика.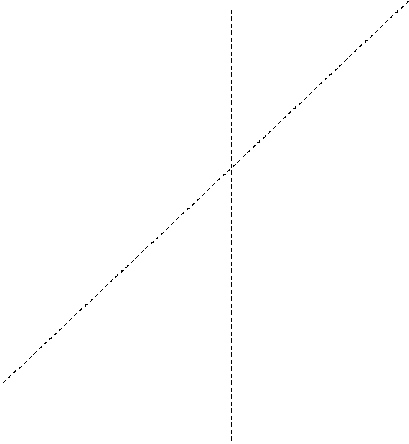
 у
у -4 4 х
-4 4 х 
 изобразить на комплексной плоскости; в виде векторов и записать в показательной и тригонометрической формах.
изобразить на комплексной плоскости; в виде векторов и записать в показательной и тригонометрической формах.
 . Для этого вычислим главный определитель системы
. Для этого вычислим главный определитель системы  и определители
и определители  , учитывая, что
, учитывая, что  – комплексное число, где
– комплексное число, где  .
.
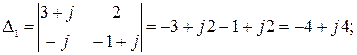

 :
: (т.к.
(т.к.  );
);

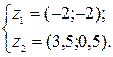
 у
у

 0, 5
0, 5

 х
х -2
-2 и аргумент
и аргумент 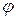 комплексных чисел
комплексных чисел  (
( или
или  ;
;  в 1 и 4 четвертях;
в 1 и 4 четвертях;  во 2 и 3 четвертях, знак «+» или «–» выбираем так, чтобы аргумент был наименьшим по модулю).
во 2 и 3 четвертях, знак «+» или «–» выбираем так, чтобы аргумент был наименьшим по модулю). принадлежит 3 четверти:
принадлежит 3 четверти: (аргумент
(аргумент  );
);
 (модуль
(модуль  ).
). принадлежит 1 четверти:
принадлежит 1 четверти: ;
;

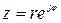 и тригонометрической
и тригонометрической  формах:
формах:
 , прямой
, прямой  и осью Ох.
и осью Ох.


