7. Классическим методом найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
7.1.
7.3.
7.5.
7.7.
7.9.
7.11.
7.13.
7.15.
7.17.
7.19.
8. (Только для профиля ТСА.) Вычислить определенный интеграл с точностью до 0, 001 путем разложения подынтегральной функции в степенной ряд и почленного интегрирования этого ряда.
8.1. 8.2.
8.3. 8.4.
8.5. 8.6.
8.7. 8.8.
8.9. 8.10.
8.11. 8.12.
8.13. 8.14.
8.15. 8.16.
8.17. 18.
8.19. 8.20.
9. (Только для профилей ЭОЭТ и ЭОП.)Разложить заданную функцию
9.1. 9.2.
9.3. 9.4.
9.5. 9.6.
9.7. 9.8.
9..9. 9.10.
9.11. 9.12.
9.13. 9.14.
9.15. 9.16.
9.17. 9.18.
9.19. 9.20.
10. Дана функция двух переменных
1) экстремум функции
2) А (1; –2);
3) наибольшую скорость возрастания функции А (1; –2).
10.1.
10.2.
10.3.
10.4.
10.5.
10..6.
10.7.
10.8.
10.9.
10.10.
10.11.
10.12.
10.13.
10.14.
10.15.
10.16.
10.17.
10.18.
10.19.
10.20.
11. Вычислить массу материальной пластинки треугольной формы с вершинами О А В n – предпоследняя, а
12. а) (Только для профиля ТСА.)Вычислить работу, совершаемую переменной силой М (1; 2) и N (3; 5).
б) (Только для профилей ЭОЭТ и ЭОП.) Проверить, что векторное поле М (1; 2) в точку N (3; 5).
12.1.
12.2.
12.3.
12.4.
12.5.
12.6.
12.7.
12.8.
12.9.
12.10.
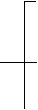
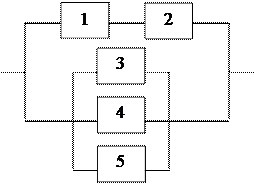
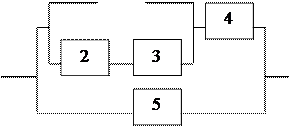
13. Найти вероятность безотказной работы участка цепи, если известно, что каждый
14. Произведена выборка 90 деталей из текущей продукции токарного автомата. Проверяемый размер деталей X измерен с точностью до одного миллиметра. Результаты измерений приведены в таблице.
1) Построить статистическое распределение выборки.
2) Выполнить точечные оценки среднего значения
3) Построить гистограмму относительных частот, установив статистический (эмпирический) закон распределения.
4) На том же чертеже построить кривую нормального распределения с параметрами
14.1.
113.00
110.84
109.48
111.24
112.04
113.56
112.20
116.12
114.76
111.64
115.00
111.32
116.04
113.72
115.24
114.36
111.88
110.36
115.48
109.64
114.84
110.68
113.96
116.12
112.28
112.84
114.52
111.08
109.96
111.80
115.16
116.68
112.76
113.32
112.44
112.60
111.00
110.60
112.92
111.48
112.44
115.80
116.12
110.84
113.40
113.80
113.88
113.40
114.04
112.76
116.76
113.88
111.72
114.28
112.52
111.72
115.40
113.08
113.72
110.92
115.72
114.52
116.84
115.56
111.32
115.88
111.80
111.48
110.20
116.04
110.52
115.80
113.72
112.28
113.88
111.24
111.88
114.12
114.52
109.72
114.44
110.68
113.00
113.24
113.32
116.52
115.24
109.80
112.68
114.76
14.2.
93.72
96.60
98.04
94.92
99.32
97.96
98.36
98.44
94.92
97.08
96.84
97.56
98.84
96.12
97.24
99.40
95.08
98.60
97.16
95.48
97.72
95.88
96.20
98.04
94.84
95.24
96.92
97.80
96.52
98.84
97.08
97.96
94.44
98.76
99.16
94.84
98.84
100.12
94.04
94.20
96.84
95.56
95.32
94.28
97.64
96.68
97.64
97.80
97.32
94.44
95.00
95.40
96.20
94.76
97.40
98.92
95.80
94.52
97.24
96.12
100.44
96.92
99.16
99.48
96.60
93.80
97.56
93.80
98.84
94.20
93.80
97.80
98.20
96.68
94.92
98.52
96.84
99.56
94.04
96.12
96.12
95.80
99.16
98.04
93.96
98.76
97.40
96.44
98.36
97.80
14.3.
128.72
130.80
129.20
129.04
126.48
128.24
130.08
128.96
126.88
129.12
130.32
125.60
130.24
126.72
125.04
128.88
129.28
124.88
129.36
126.96
127.76
129.12
124.40
129.28
126.40
125.36
129.92
130.08
126.88
128.48
129.44
128.56
128.24
126.64
130.00
130.48
130.48
127.36
128.48
128.40
126.24
129.52
129.36
126.48
127.84
127.60
128.00
124.48
129.20
126.96
129.92
128.72
129.68
126.88
130.80
128.88
128.96
127.04
128.56
126.48
129.68
125.44
131.68
126.96
124.64
125.12
127.04
128.56
127.44
129.12
128.24
124.88
130.80
126.88
130.64
130.00
125.60
127.84
129.60
127.12
127.44
131.04
125.44
129.68
124.88
126.72
127.84
127.84
126.32
127.92
14.4.
141.16
135.24
136.52
142.12
139.64
141.72
136.92
141.24
138.52
136.92
139.00
137.48
140.76
141.16
139.08
141.32
138.12
137.08
141.00
140.84
138.44
139.80
137.56
140.04
138.92
139.32
139.88
139.56
138.60
136.60
138.36
138.52
138.28
138.92
139.08
139.00
141.24
138.28
138.76
136.68
137.88
135.48
138.52
139.08
137.24
136.12
138.92
138.76
139.40
137.88
140.20
141.24
135.96
138.36
138.60
137.32
140.52
141.32
136.84
138.04
138.84
139.72
138.04
141.00
140.92
138.84
138.84
138.68
137.48
135.72
141.88
137.16
136.28
142.04
140.84
136.44
139.16
138.52
140.84
142.04
137.80
139.00
137.88
140.92
138.60
139.64
139.64
136.84
138.44
139.80
14.5.
66.52
61.88
62.20
61.16
59.32
66.36
63.08
62.52
64.76
65.24
60.52
64.52
63.64
64.92
66.36
66.44
59.80
61.16
59.56
61.16
62.60
65.08
63.64
64.04
66.44
62.28
62.20
65.16
62.28
65.24
63.40
63.96
61.48
66.52
64.04
59.80
59.64
61.96
65.24
65.56
62.68
61.56
63.96
64.12
64.36
62.76
60.60
63.40
61.64
62.52
65.32
63.96
61.40
61.88
63.88
64.44
63.00
61.72
64.84
65.08
62.52
62.92
59.56
62.84
64.12
63.80
62.36
64.04
63.24
65.56
63.24
60.20
60.44
63.64
62.12
63.80
63.00
64.20
63.48
62.20
65.88
61.72
61.48
62.52
65.48
59.08
61.00
64.52
64.44
61.16
14.6.
102.00
99.76
100.40
102.16
102.56
100.40
101.60
98.16
101.84
101.36
102.96
100.80
97.60
99.68
99.20
99.04
99.44
100.80
100.08
102.32
100.56
99.44
99.52
99.84
100.48
97.60
98.32
99.44
101.60
99.84
99.68
101.04
97.68
99.12
99.92
103.28
99.84
99.04
103.04
102.00
103.12
100.88
99.04
99.12
101.60
101.76
99.28
98.64
97.68
99.04
102.96
98.32
97.68
98.64
96.96
97.92
99.52
96.80
102.24
102.00
101.44
99.68
99.84
100.88
97.36
101.20
99.84
97.92
97.36
99.76
101.20
98.64
101.36
98.96
98.40
102.80
99.60
98.64
101.84
102.08
99.44
100.16
98.00
103.28
100.40
103.60
101.04
101.52
100.56
101.28
14.7.
109.84
109.12
104.08
106.00
108.08
110.40
106.96
108.40
105.60
108.56
105.92
110.80
109.28
108.80
109.12
109.12
106.80
106.64
108.32
109.44
105.84
104.96
111.04
105.84
109.36
105.92
110.64
105.28
107.44
107.04
110.96
108.00
107.60
107.76
106.88
107.20
108.24
108.72
104.80
108.00
109.04
104.64
107.60
109.68
110.64
108.00
110.88
106.24
108.88
107.76
108.64
107.92
106.32
105.84
107.60
106.72
108.00
108.56
108.56
107.20
109.44
108.24
105.52
107.28
106.96
108.00
106.24
106.40
106.32
107.60
107.44
109.84
109.68
106.64
105.68
108.88
104.16
108.56
106.40
107.52
108.88
107.60
109.68
108.72
108.48
106.00
108.72
109.84
109.60
108.16
14..8.
131.68
133.20
128.96
128.72
132.16
129.12
131.52
131.52
131.52
132.48
129.36
128.32
127.44
133.36
130.48
130.72
131.44
128.88
128.40
128.32
128.56
132.56
128.80
129.60
130.48
129.04
133.12
130.16
128.56
130.80
133.44
133.28
126.56
129.52
132.24
129.92
130.08
131.12
129.84
131.44
128.24
129.92
132.40
128.80
128.00
130.88
131.20
128.64
127.60
132.00
129.20
129.92
130.24
130.40
133.60
132.64
131.28
129.68
129.92
128.64
132.64
131.68
128.32
128.40
132.16
128.72
127.04
130.96
129.04
130.32
128.32
129.92
128.56
130.48
129.52
128.96
130.64
131.52
127.76
129.36
129.92
131.92
130.88
132.88
128.64
131.84
128.56
130.56
130.48
130.00
14.9.
45.96
48.12
48.84
47.00
47.48
45.32
45.48
47.80
47.08
45.16
48.76
48.04
45.48
46.36
47.08
44.92
46.04
46.36
50.04
50.04
45.72
46.84
45.24
47.00
45.48
47.80
45.64
45.16
45.88
49.56
46.60
48.12
45.24
48.60
46.60
48.20
47.16
46.52
46.68
47.40
45.16
47.32
49.56
45.24
46.92
49.96
46.60
46.44
49.24
44.36
45.80
49.88
46.12
48.20
47.56
45.96
47.24
47.00
44.84
48.60
46.44
47.24
46.52
43.96
48.36
48.84
48.12
45.16
46.60
45.72
45.00
46.36
48.52
44.92
45.80
50.12
48.04
46.12
46.36
49.32
47.80
46.28
46.36
43.64
43.16
44.36
44.04
47.64
46.68
44.20
14.10.
124.32
126.80
125.12
126.24
128.24
127.84
125.12
125.68
126.96
129.28
122.48
126.48
127.12
124.40
125.60
125.68
125.12
128.00
125.20
125.76
126.64
127.92
123.84
124.88
127.28
124.24
126.24
124.32
124.96
124.80
127.76
125.52
128.56
126.32
127.92
123.12
127.84
126.40
126.64
127.04
127.20
129.20
124.56
127.44
127.68
125.84
125.36
127.28
123.04
127.84
124.80
126.48
126.32
125.92
126.00
123.84
127.84
126.72
124.32
125.20
125.20
126.96
126.72
126.24
126.72
127.12
128.48
124.56
128.16
127.76
126.00
128.40
123.28
124.08
125.20
127.68
125.44
128.48
125.52
123.92
127.60
125.84
128.88
124.88
124.56
124.40
122.96
129.04
125.60
127.68
14.11.
108.56
109.36
109.36
112.80
111.52
110.32
108.56
112.56
109.92
108.64
109.44
112.00
110.32
110.08
108.40
110.32
108.16
110.08
108.80
109.60
107.44
110.72
106.96
108.88
112.88
107.52
110.64
109.76
111.84
106.72
107.12
110.56
109.04
108.56
108.64
111.92
111.28
109.20
110.72
107.52
111.68
108.72
109.36
110.32
109.92
111.36
111.04
110.40
112.64
111.92
111.52
107.12
111.76
111.76
108.32
110.24
111.20
110.32
106.16
111.36
111.60
111.76
110.24
110.88
113.84
112.32
109.04
108.16
106.32
109.52
107.20
113.60
113.68
111.68
109.60
109.12
109.84
109.68
110.40
109.60
110.24
112.24
106.80
110.08
110.96
111.60
110.96
111.28
113.92
111.60
14.12.
67.36
63.76
64.32
66.48
64.96
64.56
62.48
66.16
64.80
65.28
63.36
62.16
62.64
64.24
67.92
62.64
63.68
65.84
62.08
65.04
62.88
66.08
62.48
63.60
61.44
67.84
65.60
65.36
66.08
67.36
65.36
60.96
64.72
64.48
61.28
67.76
66.56
65.44
65.44
61.44
63.52
65.84
64.08
66.48
66.08
66.48
63.20
67.52
63.92
62.96
64.00
62.56
63.12
64.72
65.04
64.48
66.40
65.92
62.80
62.32
62.56
64.24
62.64
64.64
63.20
64.96
65.36
61.84
62.72
65.44
65.12
63.92
67.92
61.20
61.60
65.84
64.88
65.52
62.96
67.68
65.44
65.60
62.72
61.12
66.32
64.56
65.20
65.76
65.76
65.68
14.13.
140.56
139.92
136.80
140.00
136.32
138.56
137.84
141.36
140.64
137.44
134.56
140.48
136.32
135.60
139.52
138.96
139.04
137.84
137.12
135.76
141.92
138.16
137.92
137.92
135.52
139.20
136.72
136.64
140.64
135.36
135.76
137.44
136.96
139.12
137.28
138.40
139.28
138.40
137.36
137.68
138.48
139.36
134.80
139.04
140.16
139.12
139.20
138.32
140.00
140.56
139.20
138.72
137.84
137.84
140.32
140.64
137.12
138.72
136.96
136.40
141.04
138.00
140.48
138.88
136.32
137.12
139.04
135.12
137.76
139.12
141.28
135.04
137.52
134.08
139.60
138.08
137.12
135.68
135.52
136.00
137.12
136.56
135.04
137.76
134.88
137.84
141.12
137.20
137.76
138.72
14.14.
102.92
104.60
99.56
104.20
100.52
102.28
104.60
103.08
105.24
104.36
102.92
100.36
102.60
100.36
101.64
103.64
104.44
101.88
104.20
100.36
103.56
102.20
103.16
101.48
100.36
103.08
101.48
101.40
103.32
100.60
105.40
102.20
103.16
103.72
103.80
102.84
100.76
102.76
105.80
106.60
105.96
101.80
99.48
105.16
101.16
100.92
106.12
103.24
105.96
102.76
106.84
100.68
103.08
105.40
102.76
102.52
105.48
105.56
103.00
103.40
104.68
101.32
104.36
101.64
104.68
105.40
102.20
101.64
103.32
103.72
100.28
104.04
104.92
103.32
101.08
100.44
101.32
103.96
105.16
103.08
102.68
104.84
102.68
102.44
101.88
104.60
106.52
103.48
103.72
103.80
14.15.
70.16
72.88
70.16
71.84
72.32
71.36
71.92
73.52
73.92
74.40
72.56
74.80
75.28
70.16
69.36
70.56
72.56
68.32
70.16
69.60
75.12
73.12
72.32
71.28
74.16
72.32
74.16
72.32
73.12
72.16
70.56
71.44
70.24
70.48
73.20
68.88
72.72
71.92
71.12
73.20
72.64
72.88
73.12
71.60
74.24
70.88
72.64
72.40
70.64
74.00
73.44
73.12
73.20
70.40
75.84
72.24
72.56
71.68
73.76
73.04
70.80
72.48
73.60
68.24
71.12
73.60
74.72
71.92
73.92
69.44
73.52
69.92
70.32
70.96
69.84
70.72
70.08
74.48
75.12
69.28
70.88
75.84
70.40
70.96
73.76
71.92
70.00
70.32
72.32
71.36
14.16.
46.60
43.96
46.68
46.68
43.24
45.16
46.20
45.40
44.76
41.80
46.04
45.64
45.96
43.64
43.16
47.00
46.60
46.36
45.80
45.96
42.92
45.56
44.60
47.08
44.20
44.04
46.36
45.32
41.72
44.04
48.04
44.92
41.56
46.12
46.52
44.92
41.64
45.56
41.48
47.00
46.04
44.68
43.72
45.72
48.12
46.68
45.32
45.56
43.96
45.08
48.60
44.60
48.92
42.36
44.84
48.12
48.20
43.80
43.64
43.80
44.36
45.32
43.72
44.28
46.84
44.20
43.88
45.96
44.20
44.36
45.96
43.00
43.32
47.00
44.44
43.64
44.44
45.80
47.48
47.56
45.56
41.32
44.92
43.16
45.72
46.20
42.92
41.56
44.28
44.28
14.17.
108.16
107.68
106.72
109.92
109.28
107.76
105.20
107.28
110.00
109.20
108.16
110.32
105.92
108.64
107.12
107.12
109.52
106.88
105.76
105.12
107.52
107.84
106.32
107.68
106.00
108.64
107.36
108.48
106.96
109.68
108.88
104.24
110.24
106.08
106.88
108.56
107.76
108.24
107.44
105.04
107.12
108.32
106.32
108.64
109.76
109.12
104.40
108.64
109.28
107.68
105.04
109.04
106.80
108.40
109.92
108.80
106.16
111.68
110.16
108.08
110.16
107.20
108.32
109.76
106.72
110.96
109.12
109.28
107.20
108.80
109.36
109.52
107.52
108.80
106.96
108.32
109.12
104.72
111.76
106.72
107.04
106.80
108.48
105.04
110.08
104.64
108.08
106.72
110.56
110.72
14.18.
115.24
111.96
115.96
115.00
113.96
115.56
113.96
112.12
116.04
115.32
118.20
113.40
113.96
115.16
111.32
111.16
117.16
115.88
116.20
115.40
111.96
111.96
115.08
116.44
113.08
118.52
111.00
114.52
113.16
114.04
117.48
111.56
117.16
117.08
112.04
115.08
115.72
113.16
113.00
115.24
114.28
116.20
111.40
113.56
114.60
112.92
114.92
112.20
114.68
113.00
117.00
114.28
113.72
112.60
115.64
113.32
114.52
114.28
115.72
118.76
114.76
117.08
115.88
117.96
114.44
112.52
113.88
114.76
115.64
115.32
113.24
114.12
116.44
115.16
114.20
118.44
115.48
114.52
115.96
115.32
115.16
112.92
114.20
113.24
117.00
115.72
115.24
114.52
113.16
111.08
14.19.
56.76
57.72
58.84
57.72
56.60
58.84
55.00
55.80
59.00
53.24
60.04
57.88
53.16
59.40
57.32
54.84
59.32
55.08
56.44
56.52
58.12
56.36
56.44
57.00
57.64
57.32
57.96
55.00
57.16
57.48
57.00
56.76
59.16
55.40
57.56
57.24
55.32
56.60
54.76
58.04
56.20
56.60
55.64
58.28
56.76
54.20
59.40
58.20
54.28
56.28
55.96
55.88
58.44
55.80
60.20
56.84
59.72
54.12
60.44
56.68
57.80
56.20
55.80
58.84
54.60
60.92
55.96
58.28
56.12
59.40
54.76
57.48
58.28
53.32
58.84
55.24
55.64
56.68
56.44
58.92
59.72
58.60
55.08
54.84
53.40
57.24
57.08
56.20
58.52
56.52
14.20.

 7.2.
7.2. 
 7.4.
7.4. 
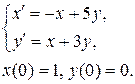 7.6.
7.6. 
 7.8.
7.8. 
 7.10.
7.10. 
 7.12.
7.12. 
 7.14.
7.14. 
 7.16.
7.16. 
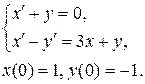 7.18.
7.18. 
 7.20.
7.20. 
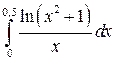 8.2.
8.2. 
 8.4.
8.4. 
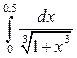 8.6.
8.6. 
 8.8.
8.8. 
 8.10.
8.10. 
 8.12.
8.12. 
 8.14.
8.14. 
 8.16.
8.16. 
 8. 18.
8. 18.  .
. 8.20.
8.20. 
 в ряд Фурье по синусам на отрезке
в ряд Фурье по синусам на отрезке  .
.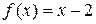 . 9.2.
. 9.2. 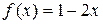 .
. . 9.4.
. 9.4.  .
. . 9.6.
. 9.6. 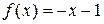 .
. . 9.8.
. 9.8.  .
. . 9.10.
. 9.10.  .
. . 9.12.
. 9.12.  .
. . 9.14.
. 9.14.  .
. . 9.16.
. 9.16.  .
. . 9.18.
. 9.18.  .
. . 9.20.
. 9.20.  .
. . Найти:
. Найти: в точке А (1; –2);
в точке А (1; –2); .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. , А (
, А ( , 0) и В (0,
, 0) и В (0,  ), поверхностная плотность которой в точке М(х.y) равна δ =х+у. Здесь n – предпоследняя, а
), поверхностная плотность которой в точке М(х.y) равна δ =х+у. Здесь n – предпоследняя, а  – последняя цифра учебного шифра.
– последняя цифра учебного шифра. по прямой, соединяющей точки М (1; 2) и N (3; 5).
по прямой, соединяющей точки М (1; 2) и N (3; 5). .
. .
. .
. .
. .
.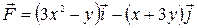 .
. .
. .
. .
. .
. -ый элемент работает независимо от других с вероятностью
-ый элемент работает независимо от других с вероятностью  (
( .
.
































 и дисперсии
и дисперсии  случайной величины
случайной величины  .
. и
и  и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения.
и проанализировать, хорошо ли статистические данные описываются нормальным законом распределения.


