Решение. Изобразим пластинку на плоскости xOy
Изобразим пластинку на плоскости xOy.
Масса неоднородной пластинки выражается через двойной интеграл по формуле: В нашем случае область D - треугольник ОАВ, Запишем уравнение прямой АВ, используя уравнение прямой в отрезках:
Вычислим массу m, переходя от двойного к повторному интегралу:
12. а) (Только для профиля ТСА.)Вычислить работу, совершаемую переменной силой
б) (Только для профилей ЭОЭТ и ЭОП.) Проверить, что векторное поле
Решение. а) Для того чтобы найти работу, совершаемую переменной силой
по прямой, соединяющей точки М (1; 1) и N (2; 3). Запишем уравнение прямой, проходящей через две данные точки:
После преобразований получаем: Перейдем от криволинейного интеграла к определенному, подставляя полученные нами выражения для y и dy и учитывая, что Тогда работа A примет вид
N
1 M
0 1 2 х
б) Векторное поле имеет вид
Производные совпадают, откуда следует, что поле Потенциал векторного поля
Для нашего случая
то есть потенциал данного поля равен
Проверим, правильно ли мы нашли потенциальную функцию. Для этого должны выполняться следующие условия:
В нашем случае:
В потенциальных полях работа A силы В нашем случае
13. Найти вероятность безотказной работы участка цепи, если известно, что каждый
Решение. Участок цепи будет работать безотказно, если работают блоки 1–2 и 3–4–5–6 (последовательное соединение). Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следовательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 исправен.
Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хотя бы в одном из случаев: исправны элементы 3 и 4, исправен элемент 5, исправен элемент 6.
надежность блока 3–4–5–6. Следовательно,
14. Измерены диаметры Таблица 1
Выполнить статистическую обработку результатов измерений по следующему плану. 1) Построить вариационный ряд. 2) Найти точечные оценки математического ожидания (генеральной средней 3) Построить гистограмму относительных частот. 4) На том же чертеже построить кривую нормального распределения и провести анализ соответствия выборочных данных нормальному закону распределения случайной величины Х.
|

 у
у В
В 0 А х
0 А х .
. .
.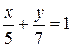 , откуда получаем
, откуда получаем  ; область D задаётся как решение системы неравенств
; область D задаётся как решение системы неравенств 
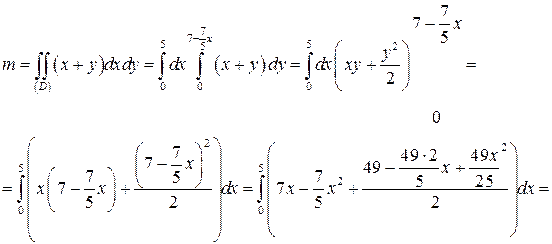

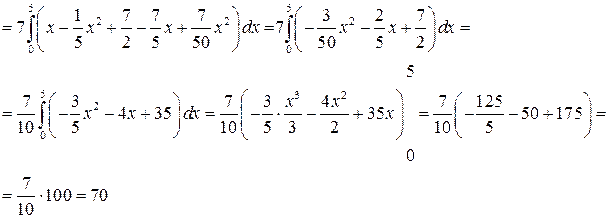
 по прямой, соединяющей точки М (1; 1) и N (2; 3).
по прямой, соединяющей точки М (1; 1) и N (2; 3). при переходе из точки М (1; 2) в точку N (3; 5).
при переходе из точки М (1; 2) в точку N (3; 5).
 .
.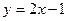 , поэтому
, поэтому  .
. .
.
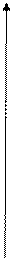 у
у 3
3
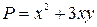 ,
, 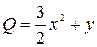 . Найдем частные производные
. Найдем частные производные  .
.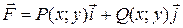 находим по формуле
находим по формуле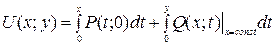 .
.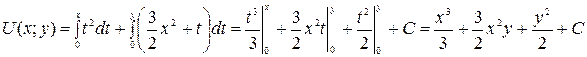 ,
, .
. .
.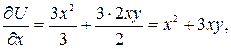 по условию
по условию  ,
, по условию
по условию 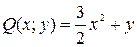 .
. .
. .
. -ый элемент работает независимо от других с вероятностью
-ый элемент работает независимо от других с вероятностью  (
(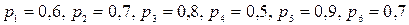 .
.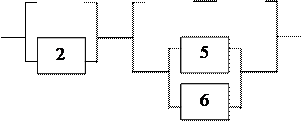
 – надежность блока 1–2.
– надежность блока 1–2.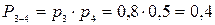 – вероятность безотказной работы блока 3–4.
– вероятность безотказной работы блока 3–4.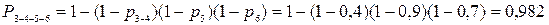 –
– – искомая надежность участка цепи.
– искомая надежность участка цепи. для 90 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1.
для 90 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 1. ) и дисперсии
) и дисперсии  случайной величины (признака)
случайной величины (признака) 


