Торсионы
Торсионы широко используются в независимых подвесках. Их основными преимуществами являются высокая энергоемкость, оптимальная компоновка, защищенность от механических Для двухрычажной подвески с одним торсионом (рис. 10.10) максимальный момент на валу упругого элемента Мшх =Мст(Ртах /(рст, _ РЧ момент от действия статической нагрузки
Мст =Pcmr2 cos а, где фст, < pmax - соответственно статический и максимальный углы закрутки упругого элемента, Pcm - вертикальная сила, действующая на рычаг подвески при статическом нагружении, r2 - длина нижнего рычага, а - угол наклона рычага. Пренебрегая другими видами деформаций, торсионы рассчитывают на кручение. Диаметр стержня d=3/^ » п[т], (10.7) где [т] - допускаемое касательное напряжение ([т] = 850...950МПа). Максимальный скручивающий момент Mmax = W[T], Mmax = I p? mJG / L, (10.8) где W = nd3/16 - полярный момент сопротивления сечения торсиона, I =nd4/32- полярный момент инерции сечения стержня, G - модуль сдвига материала торсиона. Из равенств правых частей выражений (10.8) можно получить формулу для определения рабочей длины вала упругого элемента
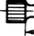
L = 0, 5dG^max/[T] Максимальный момент при скручивании пучкового торсиона с круглыми стержнями (рис.10.11, а)
где ij - число прутков в ряду, j - номер ряда в пучке торсиона (при j = 0, i0 = 1, р0 = 0), E - модуль упругости материала стержней торсиона, Iy = nd4 /64- осевой момент инерции сечения прутка, pj - расстояние между осями стержня и симметрии пучка.
а) б)
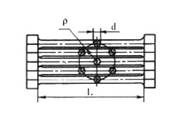
Рис.10.11. Схема торсиона: а - пучкового; б - пластинчатого Подставляя в выражение (10.9) Iр и Iy, получим выражение для определения диаметра прутка d = 2 2 -— _. (10.10) 2
0n< PrnaxLp I ij + 3EnSin0, 5^max I ij Pj j=0
Напряжения в стрежнях пучка торсиона следует определять по пруткам, расположенных на периферии, так как кроме кручения они испытывают изгиб. Максимальные напряжения прутка: касательное Tmax = 0, 5dG^max/ L, изгиба amax = 3EdPj Sin0, 5^max / L', суммарное a! max = Vaix + 3Tmax. (10.11) Если известны конструктивные параметры пучкового торсиона Pj, j, то, задаваясь максимальным напряжением аъmax, углом закрутки pmax и решая совместно уравнения (10.10) и (10.11), определим диаметр прутка d и рабочую длину L торсиона. Допускаемые напряжения для пучкового торсиона значительно выше. Чем для торсиона круглого сечения, и составляют 1000...1300 МПа. Расчет пластинчатого торсиона (рис. 10.11, б), имеющего г пластин, основан на применении выражений для момента инерции Ik и сопротивления Wk сечения пластины при кручении, которые справедливы при отношении h / b = m > 4: Wk = (m - 0, 63)b3/3, Ik = (m - 0, 63)b4/3. (1012) Из системы (10.12) можно определить b = ^3Wk /(m - 0, 63). По максимальному касательному напряжению на длинной стороне пластины и числу г пластин можно определить момент сопротивления Wk = Mmax/(lTmax) и рабочую длину пластины L = GIJVmax / Mmax = G^max / Tmax ■ Диаметр головки торсиона dr = (1, 2...1, 3)d, длина lr = (0, 9...1, 3)d. Изготавливают торсионы из рессорно-пружинных сталей типа 50ХФА и 45НХМФА.
|

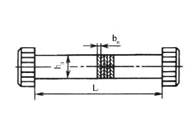
 Рис.10.10. Расчетная схема двухрычажной подвески с одним торсионом
Рис.10.10. Расчетная схема двухрычажной подвески с одним торсионом