Решение. Выделим механическую систему (см
Выделим механическую систему (см. рис. 3.5), которая состоит из двух тел: электродвигателя 1 и груза 2. Внешними силами, действующими на систему (см. рис. 3.6), являются: вес электродвигателя
Запишем выражение для теоремы о движении центра масс системы в векторной форме
и в проекциях на оси координат
Определим проекции внешних действующих сил и запишем дифференциальные уравнения движения центра масс системы в выбранной системе координат
В этих уравнениях
где
Теперь найдем значения вторых производных
с учетом которых получим выражения
откуда
Далее определим силу давления на горизонтальную плоскость: – максимальную
при – минимальную
при Следует отметить, что при отсутствии крепления в вертикальном направлении корпус электродвигателя оторвется от плоскости при давлении
Максимальную горизонтальную силу давления на болты найдем по формуле
при условии, что Теперь получим искомое уравнение движения электродвигателя по горизонтальной плоскости при отсутствии крепления болтами. С учетом того, что выбранная механическая система в начальный момент времени была неподвижна, запишем
В этом случае выполняется закон сохранения движения центра масс в проекции на ось Ох. Так как по условию для Определим координаты центра масс системы и приравняем их: – в начальном положении при значениях
– в текущем положении при значениях
Поскольку
откуда окончательно получим
Следовательно, корпус электродвигателя в случае отсутствия креплений болтами совершает гармонические колебания с амплитудой Теперь для получения уравнения движения электродвигателя по горизонтальной плоскости при отсутствии крепления болтами воспользуемся теоремой об изменении количества движения системы.
Запишем выражение для теоремы об изменении количества движения системы в векторной форме:
В проекции на ось Ox декартовой системы координат оно выглядит следующим образом
Поскольку
Проекция скорости корпуса электродвигателя на ось Ох
где
откуда
Для нахождения уравнения движения электродвигателя по горизонтальной плоскости необходимо проинтегрировать уравнение (3.5)
где С – постоянная интегрирования, определяемая из начальных условий, при
что совпадает с решением, полученным с помощью теоремы о движении центра масс.
|

 , вес груза
, вес груза  , суммарные горизонтальные реакции болтов
, суммарные горизонтальные реакции болтов  и вертикальные реакции
и вертикальные реакции  горизонтальной плоскости.
горизонтальной плоскости.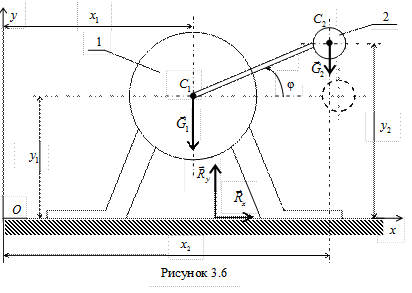

 .
. .
. ,
, и
и  – координаты центра масс электродвигателя 1 и груза 2 соответственно. Для случая, когда электродвигатель закреплен, эти координаты вычисляют следующим образом
– координаты центра масс электродвигателя 1 и груза 2 соответственно. Для случая, когда электродвигатель закреплен, эти координаты вычисляют следующим образом
 ,
, ,
, .
.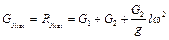
 ;
;
 .
. < 0. Угловая скорость вала электродвигателя при этом составит
< 0. Угловая скорость вала электродвигателя при этом составит < 0; ω >
< 0; ω >  .
.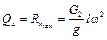
 .
. .
. то
то  , т.е. системы координаты центра масс в процессе движения неизменны.
, т.е. системы координаты центра масс в процессе движения неизменны.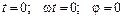
 ;
;

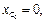 то
то ,
, .
. и циклической частотой, равной угловой скорости ω вращения вала.
и циклической частотой, равной угловой скорости ω вращения вала.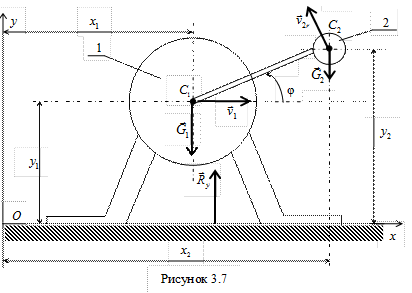

 ;
;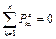 , то выполняется закон сохранения количества движения в проекции на ось Ох. Так как по условию при
, то выполняется закон сохранения количества движения в проекции на ось Ох. Так как по условию при  то
то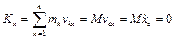 . (3.4)
. (3.4) (см. рис. 3.7). В соответствии с теоремой сложения скоростей точки при сложном движении абсолютная скорость ее равна геометрической сумме переносной и относительной скоростей. Поэтому проекцию абсолютной скорости груза 2 на ось Ох найдем по формуле
(см. рис. 3.7). В соответствии с теоремой сложения скоростей точки при сложном движении абсолютная скорость ее равна геометрической сумме переносной и относительной скоростей. Поэтому проекцию абсолютной скорости груза 2 на ось Ох найдем по формуле ,
, – численное значение относительной скорости груза по отношению к корпусу электродвигателя,
– численное значение относительной скорости груза по отношению к корпусу электродвигателя,  . Подставляя полученное выражение в уравнение (3.4), найдем
. Подставляя полученное выражение в уравнение (3.4), найдем ,
,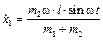 . (3.5)
. (3.5) ,
, . В нашем случае
. В нашем случае 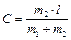 и окончательно искомое уравнение движения примет вид
и окончательно искомое уравнение движения примет вид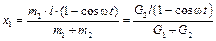 ,
,


