Решение. Выберем систему координат и изобразим (снаряд) точку М в произвольном положении
Выберем систему координат и изобразим (снаряд) точку М в произвольном положении. На точку действует только постоянная сила тяжести G. Запишем дифференциальные уравнения движения точки:
В данном случае
Начальные условия в момент времени
Дважды проинтегрируем дифференциальные уравнения движения точки:
Вычислив постоянные интегрирования
запишем уравнения движения снаряда:
Исключая из 1-го уравнения (3.2) время
Соответствующая этому уравнению траектория представляет собой параболу. Определим дальность полета снаряда. В момент падения егокоординаты y = 0, x = l. Из уравнения траектории (3.3) следует, что
откуда с учетом исходных данных получим
Решая квадратное уравнение, найдем При максимальной ординате полета снаряда
найдем время полета до достижения максимальной высоты снаряда
Подставляя полученное значение времени во 2-е уравнение (3.2)
и используя 1-е уравнение (3.2), определим при значении координаты
Скорость снаряда в момент его падения найдем с помощью формул для проекций скоростей на оси координат
|
. Сократив в этих уравнениях величину массы m, отличную от нуля, получим
:
.
;
;
;
.
- 
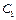из начальных условий при t = 0
, С 2 = х 0 = 0, 
, С 4 = y 0 = h,
; 
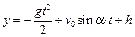. (3.2)
получим уравнение траектории движения точки в декартовой системе координат
. (3.3)
,
.
м; 
м. Так как траекторией движения снаряда является ветвь параболы с положительными абсциссами ее точек, то дальность полета 
м.
проекция скорости 
. Из уравнения
с.
м
время полета снаряда
с.
м/с.
