Общие теоремы динамики
2.5.1. Теорема о движении центра масс. Закон сохранения движения центра масс Если на k -ю материальную точку, принадлежащую механической системе, действуют внешние и внутренние силы, то, суммируя по всем точкам системы и учитывая свойства внутренних сил
получим выражение для теоремы о движении центра масс
Сформулируем теорему о движении центра масс: «Центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему». В проекциях на оси декартовой системы координат выражение (2.37) запишем следующим образом
Из приведенной теоремы следует закон сохранения движения центра масс: «Если геометрическая сумма внешних сил, действующих на систему, равна нулю Если при тех же условиях в начальный момент времени
Если при тех же условиях проекция начальной скорости на какую-либо из координатных осей (например, ось Ох) 2.5.2. Теорема об изменении количества движения системы. Закон сохранения количества движения Теорему об изменении количества движения системы можно сформулировать следующим образом: «Производная по времени от вектора количества движения системы равна геометрической сумме внешних сил, действующих на систему». Выражение для этой теоремы в дифференциальной форме имеет вид:
В проекциях на оси декартовой системы координат оно выглядит так
Из приведенной теоремы следует закон сохранения количества движения: «Если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянен по модулю и направлению»
Если алгебраическая сумма проекций внешних сил, действующих на систему, на какую-либо из координатных осей (например, ось Oх) равна нулю, то проекция количества движения системы на соответствующую ось – величина постоянная
Выражение для рассматриваемой теоремы в интегральной форме имеет вид:
откуда следует формулировка: «Приращение количества движения системы за конечный промежуток времени равно векторной сумме действующих на систему за это время полных импульсов внешних сил». В проекциях на координатные оси (например, ось Ох) выражение (2.41) запишем следующим образом
2. 5.3. Теорема об изменении кинетического момента системы. Закон сохранения кинетического момента. Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси Сформулируем теорему об изменении кинетического момента системы: «Производная по времени от кинетического момента системы относительно некоторого неподвижного центра равна геометрической сумме моментов всех внешних сил системы относительно того же центра», т.е.
В проекциях на оси декартовой системы координат выражение (2.43) для рассматриваемой теоремы примет вид:
Из приведенной теоремы следует закон сохранения кинетического момента: «Если сумма моментов внешних сил относительно некоторой точки равна нулю, то кинетический момент системы относительно этой точки сохраняет постоянное по величине и направлению значение», т.е.
В проекциях на оси декартовой системы координат (например, ось Oz) выражение (2.45) для рассматриваемой теоремы примет вид:
Если тело вращается вокруг оси Oz, то, используя выражения (2.23) и (2.44), получим дифференциальное уравнение вращательного движения тела
2.5.4. Теорема об изменении кинетической энергии системы в интегральной форме Теорему об изменении кинетической энергии системы формулируем так: «Изменение кинетической энергии системы при некотором ее конечном перемещении равно сумме работ всех приложенных к системе внешних и внутренних сил на этом перемещении», т.е.
Это математическая запись теоремы об изменении кинетической энергии в интегральной (конечной) форме. Для неизменяемой системы, где сумма работ внутренних сил равна нулю, выражение (2.47) имеет вид:
В неизменяемой механической системе, состоящей из абсолютно твердых тел и имеющей идеальные связи, когда расстояния между точками системы остаются постоянными, сумма работ внутренних сил равна нулю. Если твердые тела соединены шарнирами без трения, то работа нормальных реакций от этих шарниров равна нулю. Если тела соединены между собой гибкими нерастяжимыми нитями, то внутренние реакции нитей равны по модулям и противоположны по направлениям, а перемещения точек нитей одинаковы и сумма работ этих реакций равна нулю. Если связь возникает за счет качения тел без проскальзывания, то точки контакта имеют одинаковые скорости и, следовательно, работы сил действия и противодействия одинаковы по значению и противоположны по знаку, а их сумма равна нулю. З адачи на применение теоремы об изменении кинетической энергии в интегральной форме с целью изучения движения механической системы рекомендуют решать в такой последовательности: 1) изобразить схематически механическую систему в начальном и конечном положениях; 2) записать выражение для теоремы об изменении кинетической энергии системы в интегральной форме; 3) определить, какие виды движений совершают тела, входящие в систему; 4) записать выражение для кинетической энергии системы в конечном положении для соответствующих видов движений ее звеньев, выразив все скорости через скорость звена, которую нужно определить; 5) показать на схеме только внешние силы, приложенные к системе, считая, что она состоит из абсолютно твердых тел, соединенных идеальными нитями; 6) вычислить сумму работ внешних сил на заданных перемещениях соответствующих точек системы, выразив их через перемещения точек звена, скорость которого нужно определить, и учитывая, что зависимость между перемещениями такая же, как и между соответствующими скоростями; 7) подставить полученные значения кинетической энергии и работ в выражение для теоремы об изменении кинетической энергии всей системы и получить искомое значение скорости.
|

 (2.36)
(2.36)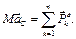 (2.37)
(2.37)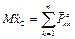 ;
;  ;
;  (2.38)
(2.38) , то
, то  – скорость центра масс есть величина постоянная по модулю и направлению».
– скорость центра масс есть величина постоянная по модулю и направлению». , то положение центра масс будет величиной постоянной, т.е.
, то положение центра масс будет величиной постоянной, т.е.  . Когда алгебраическая сумма проекций на какую-либо из координатных осей (например, ось Ох) внешних сил, действующих на систему, равна нулю, то проекция скорости центра масс на соответствующую ось – величина постоянная
. Когда алгебраическая сумма проекций на какую-либо из координатных осей (например, ось Ох) внешних сил, действующих на систему, равна нулю, то проекция скорости центра масс на соответствующую ось – величина постоянная ;
;  .
.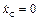 , то соответствующая координата центра масс системы
, то соответствующая координата центра масс системы  .
. (2.39)
(2.39) ;
; 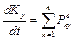 ;
;  (2.40)
(2.40) = 0;
= 0;  .
.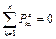 ;
;  .
.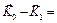
 , (2.41)
, (2.41)
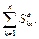 (2.42)
(2.42) (2.43)
(2.43) . (2.44)
. (2.44)
 . (2.45)
. (2.45) ;
;  .
. . (2.46)
. (2.46) . (2.47)
. (2.47) (2.48)
(2.48)


