Меры движения точки и механической системы
К мерам движения относят следующие характеристики их инертности и движения: количество движения (импульс) точки и системы, кинетический момент (момент количества движения) точки и системы относительно точки и оси, кинетическую энергию точки и системы. 2.3.1. Количество движения точки и механической системы Количеством движением точки называют векторную величину, равную произведению массы точки на ее скорость
Количеством движением механической системы называют сумму количеств движений всех ее точек
Эту величину можно выразить и через скорость центра масс (2.4)
Размерность количества движения – кг·м/с. 2.3.2. Кинетический момент точки и механической системы Кинетическим моментом или моментом количества движения материальной точки относительно некоторого центра О (рис. 2.6) называют векторную величину
Модуль кинетического момента точки
Кинетическим моментом материальной точки относительно оси называют проекцию на эту ось, например, Oz, кинетического момента относительно любой точки на этой же оси
Значение кинетического момента положительное, если вращение перпендикуляра Кинетическим моментом механической системы относительно точки или оси называют сумму кинетических моментов всех точек системы относительно точки
или оси, например, оси Ох
Кинетический момент тела вращения относительно его неподвижной оси, например, оси Oz, равен произведению момента инерции тела относительно этой оси на его угловую скорость
2.3.3. Кинетическая энергия точки и механической системы Кинетической энергией материальной точки называют скалярную величину, равную половине произведения массы точки на квадрат ее скорости
Кинетической энергией механической системы материальных точек называют сумму кинетических энергий всех точек этой системы
Она равна нулю, если все точки системы в какой-то момент времени неподвижны. Запишем выражения для кинетической энергии тела, совершающего – поступательное движение
где М – масса тела, v – его скорость;
– вращательное движение
где – плоскопараллельное движение
где Размерность кинетической энергии – Джоуль, 1 Дж = 1 Н∙ м.
|

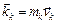 . (2.15)
. (2.15) . (2.16)
. (2.16) . (2.17)
. (2.17)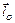 , равную векторному произведению радиус-вектора точки
, равную векторному произведению радиус-вектора точки 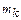 , проведенного к ней из центра О, на вектор количества движения
, проведенного к ней из центра О, на вектор количества движения  этой точки
этой точки . (2.18)
. (2.18) . (2.19)
. (2.19)
 . (2.20)
. (2.20)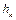 вектором
вектором  наблюдается с положительного направления, например, оси Oz, против хода часовой стрелки; отрицательное – если наоборот. Значение, равное нулю, будет иметь место, когда вектор
наблюдается с положительного направления, например, оси Oz, против хода часовой стрелки; отрицательное – если наоборот. Значение, равное нулю, будет иметь место, когда вектор  лежит в одной плоскости с соответствующей осью.
лежит в одной плоскости с соответствующей осью. (2.21)
(2.21)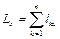 . (2.22)
. (2.22) . (2.23)
. (2.23) . (2.24)
. (2.24)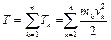 . (2.25)
. (2.25) , (2.26)
, (2.26) , (2.27)
, (2.27) – момент инерции тела относительно оси вращения, ω – его угловая скорость;
– момент инерции тела относительно оси вращения, ω – его угловая скорость;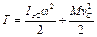 , (2.28)
, (2.28) – момент инерции тела относительно оси, проходящей через центр масс и перпендикулярной плоскости движения тела; ω – его угловая скорость; М – его масса;
– момент инерции тела относительно оси, проходящей через центр масс и перпендикулярной плоскости движения тела; ω – его угловая скорость; М – его масса;  – скорость центра масс.
– скорость центра масс.


