Геометрия масс – масс-геометрические характеристики системы
Параметры движения механической системы зависят не только ее массы, но и от распределения масс точек системы в пространстве, занимаемом системой. Это распределение определяется масс-геомет-рическими характеристиками, к которым относят центр масс системы и моменты инерции. 2.2.1. Масса и центр масс механической системы Сумму масс точек механической системы, состоящей из n материальных точек, называют массой системы
Центром масс системы называют геометрическую точку, радиус-вектор и координаты которой в выбранной системе отсчета определяют по формулам:
где Понятие центра масс значительно шире, чем понятие центра тяжести, так как центр тяжести имеет смысл только при наличии гравитационного поля, тогда как центр масс характеризует распределение масс точек в системе в данный момент времени и имеет смысл при наличии материальных объектов. Из определения центра масс следуют некоторые важные зависимости:
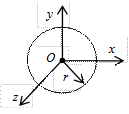
Аналогичные формулы могут быть записаны в проекциях на оси координат. 2.2.2. Моменты инерции механической системы При рассмотрении вращательных движений в динамике механической системы большое значение имеют моменты инерции, характеризующие распределение масс точек этой системы относительно точки и осей выбранной системы координат. Моменты инерции системы разделяют на осевые (относительно оси) – Осевой момент инерции – это сумма произведений массы каждой точки системы на квадрат расстояния от данной точки до соответствующей оси (рис. 2.1)
Полярный момент инерции – это сумма произведений массы каждой точки на квадрат расстояния от данной точки до полюса (точки), в нашем случае до начала координат (см. рис.2.1)
Центробежный момент инерции – это алгебраическая сумма произведений массы каждой точки на соответствующие ее координаты
Если в выбранной системе координат ( Доказано, что если тело имеет плоскость материальной симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие – расположены в этой плоскости. Если тело имеет ось материальной симметрии, то она является главной осью инерции для любой точки на этой оси. Ось инерции, проходящую через центр масс, называют центральной осью инерции, а главная ось инерции, проходящая через центр масс – главной центральной осью инерции. Иногда осевой момент инерции для ряда систем или тел сложной геометрической формы выражают в виде произведения массы системы или тела на квадрат линейной величины, которую называют радиусом инерции относительно этой оси, например, оси Oz
Здесь
т.е. радиус инерции определяет расстояние от оси до материальной точки, масса которой равна массе тела, а момент инерции данной точки относительно этой оси был равен моменту инерции тела. В системе СИ единица измерения момента инерции – Существует зависимость между моментами инерции тела относительно параллельных осей, например,
Приведем формулы для расчета осевых моментов инерции однородных тел, наиболее часто встречающихся при решении задач: – тонкого прямолинейного стержня (рис. 2.3) относительно осей, перпендикулярных его продольной оси проходящих через крайние точки стержня и через его центр масс
где М и l – соответственно масса и длина стержня; – тонкого обруча (полого цилиндра) относительно его продольной центральной оси (рис. 2.4)
где М и r – соответственно масса и радиус обруча (цилиндра); – сплошногокругового диска (цилиндра) относительно его центральной продольной оси (рис. 2.5)
где m, r – соответственно масса диска (цилиндра) и радиус его внешней окружности.
|

 . (2.2)
. (2.2) , (2.3)
, (2.3) – масса k -й точки системы;
– масса k -й точки системы;  – радиус-вектор этой точки;
– радиус-вектор этой точки;  – ее координаты.
– ее координаты. ;
; ; (2.4)
; (2.4)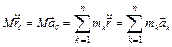 .
. ; полярные (относительно точки или полюса) –
; полярные (относительно точки или полюса) –  ; центробежные (произведения инерции) –
; центробежные (произведения инерции) –  .
. (2.5)
(2.5)
 . (2.6)
. (2.6) . (2.7)
. (2.7)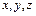 с началом в точке О) центробежные моменты инерции равны нулю, то оси этой системы называют главными осями инерции для точки О.
с началом в точке О) центробежные моменты инерции равны нулю, то оси этой системы называют главными осями инерции для точки О. или
или  . (2.8)
. (2.8) – масса тела;
– масса тела; 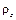 или
или  – радиус инерции относительно оси Oz,
– радиус инерции относительно оси Oz, , (2.9)
, (2.9) .
. и
и  (рис. 2.2), где ось
(рис. 2.2), где ось  , (2.10)
, (2.10) где
где  ; (2.11)
; (2.11)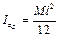 , (2.12)
, (2.12) , (2.13)
, (2.13) , (2.14)
, (2.14)