Уравнения Лагранжа 2-го рода
2.6.1. Краткие теоретические сведения Уравнения Лагранжа 2-го рода обычно применяют для исследования движения механических систем с несколькими степенями свободы, но такие исследования выходят за рамки изучаемого курса теоретической механики. Поэтому с целью приобретения некоторых навыков в составлении уравнений Лагранжа для механических систем с n степенями свободы ограничимся применением этих уравнений при определении основных кинематических и динамических параметров систем с одной степенью свободы. Уравнения Лагранжа 2-го рода для механических систем с идеальными, стационарными, голономными и удерживающими связями, имеют вид:
где q – обобщенная координата системы, однозначно определяющая ее положение (число независимых обобщенных координат соответствует числу степеней свободы системы);
где Размерность обобщенной силы зависит от размерности обобщенной координаты. Если обобщенная координата имеет размерность длины (м), то обобщенную силу измеряют в Ньютонах (Н); если обобщенная координата имеет размерность угла (рад), то сила имеет размерность момента (Н∙ м). В предлагаемых в 4-м разделе настоящего пособия заданиях кинетическая энергия системы не зависит от обобщенной координаты
2.6.2. Последовательность решения задач на уравнения Лагранжа 2-го рода Задачи, посвященные исследованию движения механических систем с одной степенью свободы с применением уравнений Лагранжа 2-го рода, рекомендуют решать в такой последовательности: 1) выбрать обобщенные координаты, линейные или угловые перемещения в зависимости оттого, что нужно определить по условию задачи – линейное или угловое ускорение; записать уравнение Лагранжа 2-го рода с учетом выбранной обобщенной координаты и обобщенной скорости; 2) изобразить механическую систему и показать на схеме все активные силы и силы трения, действующие на эту систему; 3) дать элементарное приращение соответствующей обобщенной координате системы; 4) вычислить сумму работ всех активных сил и сил трения на соответствующих элементарных перемещениях и определить обобщенную силу с учетом того, что зависимость между элементарными перемещениями такая же, как и между соответствующими скоростями; 5) вычислить кинетическую энергию системы, выразив ее через соответствующую обобщенную скорость; 6) найти частную производную от кинетической энергии по обобщенной скорости, а затем производную по времени от полученного выражения; 7) подставить найденные значения в уравнение Лагранжа и определить линейное или угловое ускорение.
Вопросы для самоконтроля
1. Что называют механической системой? 2. Какие существуют виды связей? 3. Как классифицируют силы, действующие на механическую систему? 4. Какие свойства имеют внутренние силы? 5. Что называют центром масс механической системы? 6. Какой вид имеет выражение для теоремы о движении центра масс механической системы в векторной форме? 7. Какой вид имеет выражение для теоремы о движении центра масс механической системы в проекциях на оси декартовой системы координат? 8. Какие существуют виды моментов инерции и в чем их отличие? 9. По каким формулам определяют осевые моменты инерции некоторых простейших тел? 10. Что называют кинетическим моментом механической системы? 11. Какой вид имеет выражение для теоремы об изменении кинетического момента механической системы в векторной форме? 12. Какой вид имеет выражение для теоремы об изменении кинетической энергии механической системы в интегральной форме? 13. По какой формуле определяют кинетическую энергию тела, совершающего поступательное движение? 14. По какой формуле определяют кинетическую энергию тела, совершающего вращательное движение? 15. По какой формуле определяют кинетическую энергию тела, совершающего плоскопараллельное движение? 16. Как определяют работу силы тяжести? 17. Как определяют работу силы на прямолинейном конечном перемещении? 18. Как определяют работу силы трения скольжения? 19. Как определяют работу пары сил сопротивлению качения? 20. В каком случае работа силы на прямолинейном перемещении равна нулю? 21. В каком случае работа силы тяжести равна нулю? 22. Что называют обобщенной координатой механической системы? 23. Что называют обобщенной скоростью механической системы? 24. Что называют числом степеней свободы механической системы? 25. Как выразить сумму элементарных работ системы через обобщенные силы? 26. Как определить обобщенную силу? 27. Какую размерность имеет обобщенная сила, если обобщенной координатой является линейное перемещение? 28. Какую размерность имеет обобщенная сила, если обобщенной координатой является угловое перемещение? 29. Какой вид имеет уравнение Лагранжа 2-го рода для системы с одной степенью свободы?
|

 , (2.49)
, (2.49)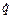 – обобщенная скорость, первая производная по времени от обобщенной координаты;
– обобщенная скорость, первая производная по времени от обобщенной координаты;  – обобщенная сила, соответствующая выбранной обобщенной координате. Ее можно найти по формуле
– обобщенная сила, соответствующая выбранной обобщенной координате. Ее можно найти по формуле , (2.50)
, (2.50) – сумма работ всех активных сил, в том числе и сил трения, на элементарном приращении
– сумма работ всех активных сил, в том числе и сил трения, на элементарном приращении  обобщенной координаты q.
обобщенной координаты q.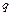 , поэтому
, поэтому и
и  .
.


