Дифференциальные уравнения движения материальной точки
Свободной называют точку, на которую не наложены связи. В противном случае точка является несвободной и тогда, согласно принципу освобождаемости от связей к точке прикладывают реакции отброшенных связей, кроме активных сил. Если на свободную точку действует система активных сил, равнодействующая которой
Полученное выражение называют основным уравнением динамикисвободной материальной точки в векторной форме. Если движение точки задано в векторной форме
и формулу (1.1) можно записать следующим образом
Нужно отметить, что в общем случае сила
Равенство (1.3) представляет собой векторное дифференциальное уравнение движения свободной материальной точки. В проекциях на оси инерциальной декартовой системы координат оно примет вид:
При движении точки в плоскости xOy, так как
Если точка движется прямолинейно вдоль какой-либо оси, например Ox, так как
В проекциях на оси (касательную, нормаль и бинормаль к траектории точки) естественной системы координат равенство (1.3) запишем следующим образом
Из кинематики известно, что
Поэтому рассматриваемые выражения примут вид:
где Если точка несвободна то на нее, кроме равнодействующей активных сил
Полученное выражение называют основным уравнением динамикинесвободной материальной точки в векторной форме. Оно принимает такой вид: – в проекциях на оси декартовой системы координат
– в проекциях на оси естественной системы координат
или
|

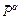 , то согласно 2-му закону Ньютона следует, что
, то согласно 2-му закону Ньютона следует, что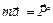 . (1.1)
. (1.1) , то, как известно из раздела кинематики,
, то, как известно из раздела кинематики, (1.2)
(1.2) . (1.3)
. (1.3) может быть функцией времени, положения и скорости точки
может быть функцией времени, положения и скорости точки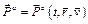 . (1.4)
. (1.4) . (1.5)
. (1.5) , систему уравнений можно записать так:
, систему уравнений можно записать так: . (1.6)
. (1.6) , получим
, получим . (1.7)
. (1.7) . (1.8)
. (1.8) . (1.9)
. (1.9)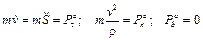 , (1.10)
, (1.10) – уравнение движения точки по соответствующей траектории; ρ – радиус кривизны траектории;
– уравнение движения точки по соответствующей траектории; ρ – радиус кривизны траектории;  – проекции равнодействующей сил, приложенных к точке на оси естественной системы координат.
– проекции равнодействующей сил, приложенных к точке на оси естественной системы координат. . Тогда уравнение (1.1) запишем так:
. Тогда уравнение (1.1) запишем так: . (1.11)
. (1.11) ; (1.12)
; (1.12) (1.13)
(1.13) . (1.14)
. (1.14)


