Решение. В рассматриваемой механической системе грузы 1, 4 совершают поступательные движения, блок 2 – вращательное
В рассматриваемой механической системе грузы 1, 4 совершают поступательные движения, блок 2 – вращательное, каток 3 – плоскопараллельное. Воспользуемся выражением для теоремы об изменении кинетической энергии в интегральной форме
В него входят слагаемые, аналогичные тем, которые рассмотрены в примере 8. В конечном положении системы кинетическая энергия складывается из суммы кинетических энергий абсолютно твердых тел 1-4, входящих в систему
Определим кинетические энергии входящих в систему тел: – груза 1
где – блока 2
где – катка 3
где – груза 4
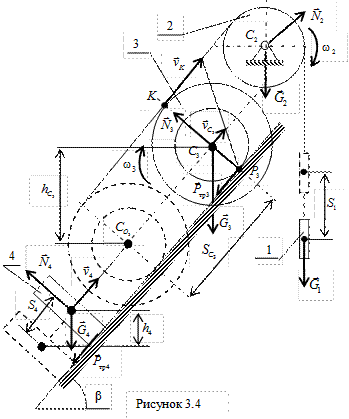
где Теперь изобразим рассматриваемую механическую систему в начальном и конечном положениях, а также все силовые факторы, действующие на эту систему (рис. 3.14). Выразим скорости тел 1-4 через угловую скорость катка
Так как каток 3 катится по наклонной плоскости без скольжения, его мгновенный центр скоростей находится в точке
откуда следует, что
или
Определим кинетическую энергию всей системы, используя кинематические зависимости, выражения для моментов инерции
В рассматриваемой механической системе работу совершают только внешние силы, которые изображены для системы, находящейся в конечном положении (см. рис. 3.14). Найдем сумму работ внешних сил на заданных перемещениях точек системы с учетом того, что груз 1 переместился по вертикали на расстояние
где
Учитывая, что зависимость между перемещениями точек такая же, как и между соответствующими скоростями
окончательно выразим сумму полной работы сил системы
Подставляя в это выражение исходные данные, получим
Далее приравнивая
и скорость его центра масс
|

 .
. .
. ,
, – скорость груза 1;
– скорость груза 1; ,
, – момент инерции блока 2 (однородного цилиндра) относительно его продольной центральной оси,
– момент инерции блока 2 (однородного цилиндра) относительно его продольной центральной оси,  ;
;  – угловая скорость блока;
– угловая скорость блока; ,
, – момент инерции ступенчатого катка 3 относительно его продольной центральной оси,
– момент инерции ступенчатого катка 3 относительно его продольной центральной оси,  ;
;  и
и  – угловая скорость и скорость центра масс катка соответственно;
– угловая скорость и скорость центра масс катка соответственно;
 – скорость груза 4.
– скорость груза 4. .
.
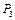 , и
, и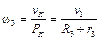 ,
, ;
;
 .
.
 .
. . Работы сил
. Работы сил  и
и  равны нулю, так как точки приложения этих сил неподвижны. Работы сил
равны нулю, так как точки приложения этих сил неподвижны. Работы сил 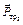 и
и  равны нулю, так как эти силы приложены в точках, которые являются мгновенными центрами скоростей. Работа силы
равны нулю, так как эти силы приложены в точках, которые являются мгновенными центрами скоростей. Работа силы  равна нулю, так как реакция наклонной плоскости перпендикулярна перемещению груза 4. Таким образом, полная работа системы складывается из суммы работ
равна нулю, так как реакция наклонной плоскости перпендикулярна перемещению груза 4. Таким образом, полная работа системы складывается из суммы работ ,
, – работы сил тяжести
– работы сил тяжести  ,
,  ,
,  соответственно,
соответственно, ;
;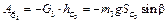 ;
;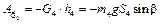 ;
; – работа силы трения
– работа силы трения  (
( ),
), .
. ,
, .
.
 , найдем угловую скорость катка 3
, найдем угловую скорость катка 3 8, 9 рад/с
8, 9 рад/с м/с.
м/с.


