Решение. Для определения углового ускорения барабана 2 выберем в качестве обобщенной координаты его угловое перемещение φ
Для определения углового ускорения
Механическая система изображена в смещенном положении с учетом положительного направления координаты φ (см. рис. 3.17), показаны все активные силы, действующие на нее: силы тяжести Найдем сумму работ всех перечисленных сил на этих элементарных приращениях
где
Так как в последней формуле сила трения груза 4
Поскольку Запишем кинематические соотношения, учитывая, что зависимость между элементарными приращениями координат такая же, как и между соответствующими скоростями
Теперь, подставляя исходные данные, посчитаем сумму элементарных работ всех сил
откуда найдем обобщенную силу, соответствующую выбранной обобщенной координате φ,
Кинетическая энергия системы складывается из кинетических энергий тел 1-4, входящих в эту систему,
Для ее вычисления нужно выразить линейные и угловые скорости точек и тел системы через обобщенную скорость – груза 1, совершающего поступательное движение,
– барабана 2, совершающего вращательное движение,
где – барабана 3, совершающего вращательное движение,
где – груза 4, совершающего поступательное движение,
где Теперь подставим все полученные выражения для кинетических энергий тел 1-4 и исходные данные в формулу для полной кинетической энергии системы
и найдем
так как обобщенная координата φ в выражение для кинетической энергии не входит. Далее определим угловое ускорение барабана 2, подставляя полученные значения в уравнение Лагранжа 2-го рода
откуда
Запишем основное уравнение динамики материальной точки в векторной форме
и в проекции на ось Ох
Подставляя исходные данные, вычислим
4. ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
|

 барабана 2 выберем в качестве обобщенной координаты его угловое перемещение φ. Тогда уравнение Лагранжа 2-го рода для координаты φ и соответственно обобщенной скорости
барабана 2 выберем в качестве обобщенной координаты его угловое перемещение φ. Тогда уравнение Лагранжа 2-го рода для координаты φ и соответственно обобщенной скорости  запишем в виде
запишем в виде .
. грузов 1, 4 и
грузов 1, 4 и  барабанов 2, 3, а также сила трения
барабанов 2, 3, а также сила трения  груза 4 о наклонную плоскость. Если положительное элементарное приращение обобщенной координаты системы
груза 4 о наклонную плоскость. Если положительное элементарное приращение обобщенной координаты системы  , то величины
, то величины  будут элементарными приращениями соответствующих координат.
будут элементарными приращениями соответствующих координат. ,
,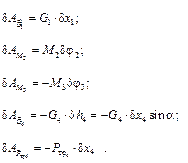
 , то
, то .
. , то работы сил
, то работы сил  также равны нулю, т.е.
также равны нулю, т.е.  .
.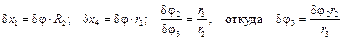 .
. =
= ,
, .
. .
. ;
; ,
, – момент инерции барабана относительно его продольной центральной оси,
– момент инерции барабана относительно его продольной центральной оси,  ;
;  – его угловая скорость,
– его угловая скорость,  ;
; ,
, – момент инерции барабана (сплошного однородного цилиндра) относительно его продольной центральной оси,
– момент инерции барабана (сплошного однородного цилиндра) относительно его продольной центральной оси, 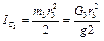 ;
;  – его угловая скорость,
– его угловая скорость,  ;
; ,
, – скорость груза,
– скорость груза,  .
.

 ,
, .
. Найдем силу натяжения троса, равную по величине реакции
Найдем силу натяжения троса, равную по величине реакции  , мысленно разрезав его и изобразив все силы, действующие на груз 1, считая груз материальной точкой (рис. 3.18).
, мысленно разрезав его и изобразив все силы, действующие на груз 1, считая груз материальной точкой (рис. 3.18). ,
, .
.



