свободы при помощи уравнения Лагранжа 2-го рода
Перед выполнением задания № 3 рекомендуется рассмотреть решения типовых задач, приведенных в подразделе 3.6 данного пособия.
Механическая система состоит из двух грузов 1, 4 и двух ступенчатых барабанов 2 весом 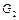 , 3 весом , 3 весом  , связанных между собой зубчатым зацеплением (рис. 4.7). К барабану 2, приводящему в движение систему, приложена пара сил, постоянный момент которой , связанных между собой зубчатым зацеплением (рис. 4.7). К барабану 2, приводящему в движение систему, приложена пара сил, постоянный момент которой  . К барабану 3 приложена пара сил, постоянный момент сопротивления которой . К барабану 3 приложена пара сил, постоянный момент сопротивления которой  . Груз 1 весом . Груз 1 весом 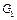 движется по шероховатой наклонной плоскости, расположенной под углом α к горизонту, при этом груз 4 весом движется по шероховатой наклонной плоскости, расположенной под углом α к горизонту, при этом груз 4 весом  перемещается по вертикали. Коэффициент трения груза 1 о наклонную плоскость – перемещается по вертикали. Коэффициент трения груза 1 о наклонную плоскость –  ; радиусы ступеней барабанов 2, 3 соответственно – ; радиусы ступеней барабанов 2, 3 соответственно – 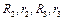 ; радиусы инерции относительно осей вращения – ; радиусы инерции относительно осей вращения –  . Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми. . Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми.
Определить согласно данным табл. 4.7 ускорение указанного тела и силу натяжения указанного троса.

Рисунок 4.7
Таблица 4.7
| Вариант
|  , Н , Н
| 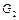 , Н , Н
|  , Н , Н
|  , Н , Н
|  , м , м
|  , м , м
|  , м , м
|  , м , м
| |
| 15 G
| 14 G
| 13 G
| 2 G
| 0, 2
| 0, 3
| 0, 2
| 0, 4
| |
| 18 G
| 12 G
| 12 G
| G
| 0, 05
| 0, 1
| 0, 2
| 0, 4
| |
| 10 G
| 16 G
| 10 G
| 0, 5 G
| 0, 2
| 0, 25
| 0, 15
| 0, 3
| |
| 12 G
| 12 G
| 12 G
| 0, 5 G
| 0, 15
| 0, 2
| 0, 1
| 0, 4
| |
| 10 G
| 13 G
| 14 G
| G
| 0, 04
| 0, 1
| 0, 2
| 0, 4
| |
| 16 G
| 14 G
| 13 G
| 2 G
| 0, 2
| 0, 3
| 0, 4
| 0, 6
| |
| 9 G
| 12 G
| 12 G
| 0, 5 G
| 0, 1
| 0, 2
| 0, 2
| 0, 4
| |
| 14 G
| 12 G
| 13 G
| 2 G
| 0, 15
| 0, 3
| 0, 1
| 0, 2
| |
| 11 G
| 15 G
| 12 G
| G
| 0, 1
| 0, 15
| 0, 2
| 0, 4
| |
| 16 G
| 13 G
| 12 G
| 2 G
| 0, 2
| 0, 4
| 0, 1
| 0, 4
| Продолжение табл. 4.7
| Вариант
|  , м , м
|  , м , м
| 
| α, град
| 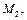

| 

| Определить
| |
| 0, 25
| 0, 3
| 0, 4
|
| 0, 2 G
| 0, 25 G
| 
| 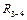
| |
| 0, 08
| 0, 3
| 0, 2
|
| 0, 1 G
| 0, 15 G
| 
| 
| |
| 0, 22
| 0, 2
| 0, 1
|
| 0, 1 G
| 0, 13 G
| 
| 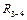
| |
| 0, 18
| 0, 3
| 0, 2
|
| 0, 2 G
| 0, 25 G
| 
| 
| |
| 0, 08
| 0, 3
| 0, 1
|
| 0, 1 G
| 0, 15 G
| 
| 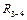
| |
| 0, 25
| 0, 5
| 0, 3
|
| 0, 3 G
| 0, 35 G
| 
| 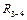
| |
| 0, 15
| 0, 3
| 0, 1
|
| 0, 2 G
| 0, 25 G
| 
| 
| |
| 0, 2
| 0, 15
| 0, 2
|
| 0, 1 G
| 0, 15 G
| 
| 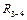
| |
| 0, 12
| 0, 3
| 0, 1
|
| 0, 3 G
| 0, 35 G
| 
| 
| |
| 0, 3
| 0, 4
| 0, 3
|
| 0, 2 G
| 0, 25 G
| 
| 
|
Механическая система состоит из грузов 1, 4, ступенчатого барабана 2 весом 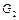 и вала 3 весом и вала 3 весом  , связанных между собой (рис. 4.8). К барабану 2, приводящему в движение систему, приложена пара сил, постоянный момент которой , связанных между собой (рис. 4.8). К барабану 2, приводящему в движение систему, приложена пара сил, постоянный момент которой  . К валу 3 приложена пара сил, постоянный момент сопротивления которой . К валу 3 приложена пара сил, постоянный момент сопротивления которой  . Груз 1 весом . Груз 1 весом 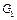 движется по шероховатой наклонной плоскости, расположенной под углом α к горизонту, при этом груз 4 весом движется по шероховатой наклонной плоскости, расположенной под углом α к горизонту, при этом груз 4 весом  перемещается по вертикали. Коэффициент трения груза 1 о наклонную плоскость – перемещается по вертикали. Коэффициент трения груза 1 о наклонную плоскость –  ; радиусы ступеней барабана 2 – ; радиусы ступеней барабана 2 – 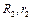 ; радиус инерции его относительно оси вращения – ; радиус инерции его относительно оси вращения –  . Вал 3 следует считать сплошным однородным цилиндром. Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми. . Вал 3 следует считать сплошным однородным цилиндром. Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми.
Определить согласно данным табл. 4.8 ускорение указанного тела и силу натяжения указанного троса.
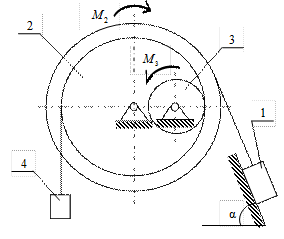
Рисунок 4.8
Таблица 4.8
| Вариант
| 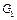 , Н , Н
| 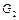 , Н , Н
|  , Н , Н
|  , Н , Н
|  , м , м
|  , м , м
|  , м , м
| |
| 16 G
| 13 G
| 12 G
| G
| 0, 25
| 0, 4
| 0, 1
| |
| 11 G
| 14 G
| 10 G
| 2 G
| 0, 1
| 0, 15
| 0, 05
| |
| 17 G
| 12 G
| 13 G
| 3 G
| 0, 15
| 0, 3
| 0, 05
| |
| 9 G
| 5 G
| 12 G
| 2 G
| 0, 3
| 0, 4
| 0, 1
| |
| 10 G
| 14 G
| 13 G
| 2 G
| 0, 2
| 0, 3
| 0, 05
| |
| 12 G
| 13 G
| 14 G
| G
| 0, 04
| 0, 1
| 0, 02
| |
| 10 G
| 5 G
| 5 G
| 2 G
| 0, 15
| 0, 3
| 0, 05
| |
| 8 G
| 16 G
| 10 G
| 0, 5 G
| 0, 2
| 0, 25
| 0, 1
| |
| 15 G
| 12 G
| 10 G
| G
| 0, 05
| 0, 1
| 0, 025
| |
| 10 G
| 14 G
| 13 G
| 2 G
| 0, 15
| 0, 3
| 0, 05
| Продолжение табл. 4.8
| Вариант
|  , м , м
| 
| α, град
| 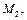 
|  
| Определить
| |
| 0, 3
| 0, 2
|
| 0, 7 G
| 0, 35 G
| 
| 
| |
| 0, 12
| 0, 1
|
| 0, 5 G
| 0, 25 G
| 
| 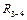
| |
| 0, 2
| 0, 1
|
| 0, 7 G
| 0, 35 G
| 
| 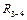
| |
| 0, 35
| 0, 2
|
| G
| 0, 45 G
| 
| 
| |
| 0, 25
| 0, 1
|
| 0, 5 G
| 0, 25 G
| 
| 
| |
| 0, 08
| 0, 2
|
| 0, 2 G
| 0, 15 G
| 
| 
| |
| 0, 25
| 0, 1
|
| 0, 3 G
| 0, 25 G
| 
| 
| |
| 0, 22
| 0, 1
|
| 0, 7 G
| 0, 35 G
| 
| 
| |
| 0, 08
| 0, 3
|
| 0, 5 G
| 0, 25 G
| 
| 
| |
| 0, 3
| 0, 15
|
| 0, 5 G
| 0, 2 G
| 
| 
| Механическая система состоит из двух грузов 1, 4 и двух ступенчатых шкивов 2, 3. (рис. 4.9). К шкиву 2 весом 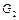 , приводящему в движение систему, приложена пара сил, постоянный момент которой , приводящему в движение систему, приложена пара сил, постоянный момент которой  . К шкиву 3 весом . К шкиву 3 весом  приложена пара сил, постоянный момент сопротивления которой приложена пара сил, постоянный момент сопротивления которой  . Груз 1 весом . Груз 1 весом 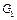 движется по вертикали, а груз 4 весом движется по вертикали, а груз 4 весом  при этом перемещается по шероховатой наклонной плоскости, расположенной под углом α к горизонту. Коэффициент трения груза 4 о наклонную плоскость – при этом перемещается по шероховатой наклонной плоскости, расположенной под углом α к горизонту. Коэффициент трения груза 4 о наклонную плоскость –  ; радиусы ступеней шкивов 2, 3 – ; радиусы ступеней шкивов 2, 3 –  ; радиусы инерции их относительно осей вращения – ; радиусы инерции их относительно осей вращения –  . Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми. . Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми.
Определить согласно данным табл. 4.9 ускорение указанного тела и силу натяжения указанного троса.
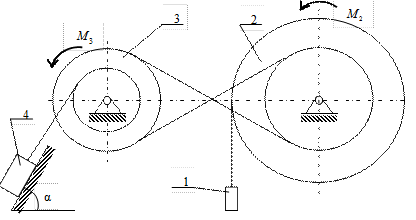
Рисунок 4.9
Таблица 4.9
| Вариант
| 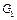 , Н , Н
| 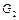 , Н , Н
|  , Н , Н
|  , Н , Н
|  , м , м
|  , м , м
|  , м , м
|  , м , м
| |
| 10 G
| 13 G
| 18 G
| 0, 5 G
| 0, 1
| 0, 6
| 0, 2
| 0, 4
| |
| 8 G
| 15 G
| 14 G
| G
| 0, 2
| 0, 4
| 0, 1
| 0, 15
| |
| 12 G
| 12 G
| 12 G
| 2 G
| 0, 1
| 0, 2
| 0, 15
| 0, 3
| |
| 14 G
| 13 G
| 12 G
| 2 G
| 0, 2
| 0, 4
| 0, 1
| 0, 2
| |
| 10 G
| 14 G
| 10 G
| G
| 0, 4
| 0, 6
| 0, 2
| 0, 3
| |
| 16 G
| 12 G
| 13 G
| 3 G
| 0, 2
| 0, 4
| 0, 04
| 0, 1
| |
| 10 G
| 10 G
| 14 G
| 2 G
| 0, 1
| 0, 4
| 0, 15
| 0, 2
| |
| 8 G
| 13 G
| 15 G
| G
| 0, 15
| 0, 3
| 0, 2
| 0, 25
| |
| 12 G
| 10 G
| 16 G
| 2 G
| 0, 2
| 0, 4
| 0, 05
| 0, 1
| |
| 15 G
| 13 G
| 12 G
| 3 G
| 0, 2
| 0, 4
| 0, 2
| 0, 3
| Продолжение табл. 4.9
| Вариант
|  , м , м
|  , м , м
| 
| α, град
| 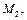

| 

| Определить
| |
| 0, 4
| 0, 3
| 0, 2
|
| 0, 3 G
| 3, 5 G
| 
| 
| |
| 0, 3
| 0, 12
| 0, 1
|
| 0, 2 G
| 1, 5 G
| 
| 
| |
| 0, 15
| 0, 2
| 0, 2
|
| 0, 4 G
| 4, 5 G
| 
| 
| |
| 0, 3
| 0, 15
| 0, 3
|
| 0, 2 G
| 2, 5 G
| 
| 
| |
| 0, 5
| 0, 25
| 0, 1
|
| 0, 1 G
| 1, 5 G
| 
| 
| |
| 0, 3
| 0, 08
| 0, 2
|
| 0, 3 G
| 3, 5 G
| 
| 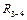
| |
| 0, 3
| 0, 18
| 0, 1
|
| 0, 4 G
| 4, 5 G
| 
| 
| |
| 0, 2
| 0, 22
| 0, 1
|
| 0, 2 G
| 2, 5 G
| 
| 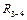
| |
| 0, 3
| 0, 03
| 0, 2
|
| 0, 1 G
| 1, 5 G
| 
| 
| |
| 0, 3
| 0, 25
| 0, 3
|
| 0, 2 G
| 2, 5 G
| 
| 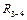
|
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Павловський М.А. Теоретична механіка.– К.: Техніка, 2002.–512с.
2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики / В 2-х т.– М.: Наука, т. 1, 1979.– 272 с.; т. 2, 1979.– 332 с.
3. Попов М.В. Теоретическая механика. Краткий курс.– М.: Наука, 1986.– 335 с.
4. Павловский М.А., Акинфиева Л.Ю., Бойчук О.Ф. Теоретическая механика. Статика. Кинематика.– М.: Наука, 1989.– 351 с.
5. Павловский М.А., Акинфиева Л.Ю., Бойчук О.Ф. Теоретическая механика. Динамика.– К.: Вища школа, 1990.– 480 с.
6. Мещерский В.И. Сборник задач по теоретической механике.–М.: Наука, 1986.– 448 с.
7. Тарг С.М. Краткий курс теоретической механики.– М.: Высшая школа, 1998.– 416 с.
8. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах / в 3-х т.– М.: Наука, 1990.– 672 с.
9. Беломытцев А.С. Краткий курс теоретической механики. Статика и кинематика / Тексты лекций для студентов заочной формы обучения всех специальностей.– Харьков: НТУ «ХПИ», 2004.– 76 с.
10. Беломытцев А.С. Краткий курс теоретической механики. Динамика / Тексты лекций для студентов заочной формы обучения всех специальностей.– Харьков: НТУ «ХПИ», 2006.– 128 с.
11. Адашевский В.М., Анищенко Г.О., Тарсис Ю.Л. Общий курс теоретической механики / Учебное пособие для студентов заочной формы обучения.– Харьков: НТУ «ХПИ», 2005.– 112 с.
12. Адашевский В.М., Анищенко Г.О., Тарсис Ю.Л. Теоретическая механика. Статика / Учебно-методическое пособие для студентов заочной формы обучения всех специальностей.– Харьков: НТУ «ХПИ», 2006.– 64 с.
13. Адашевский В.М., Анищенко Г.О., Тарсис Ю.Л. Теоретическая механика. Кинематика / Учебно-методическое пособие для студентов заочной формы обучения всех специальностей.– Харьков: НТУ «ХПИ», 2007.– 72 с.

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
ТЕХНИКА ПОСЕВА, МЕТОДЫ ВЫДЕЛЕНИЯ ЧИСТЫХ КУЛЬТУР И КУЛЬТУРАЛЬНЫЕ СВОЙСТВА МИКРООРГАНИЗМОВ. ОПРЕДЕЛЕНИЕ КОЛИЧЕСТВА БАКТЕРИЙ Цель занятия. Освоить технику посева микроорганизмов на плотные и жидкие питательные среды и методы выделения чистых бактериальных культур. Ознакомить студентов с основными культуральными характеристиками микроорганизмов и методами определения...
САНИТАРНО-МИКРОБИОЛОГИЧЕСКОЕ ИССЛЕДОВАНИЕ ВОДЫ, ВОЗДУХА И ПОЧВЫ Цель занятия.Ознакомить студентов с основными методами и показателями...
Меры безопасности при обращении с оружием и боеприпасами 64. Получение (сдача) оружия и боеприпасов для проведения стрельб осуществляется в установленном порядке[1].
65. Безопасность при проведении стрельб обеспечивается...
|
ОСНОВНЫЕ ТИПЫ МОЗГА ПОЗВОНОЧНЫХ Ихтиопсидный тип мозга характерен для низших позвоночных - рыб и амфибий...
Принципы, критерии и методы оценки и аттестации персонала
Аттестация персонала является одной их важнейших функций управления персоналом...
Пункты решения командира взвода на организацию боя. уяснение полученной задачи; оценка обстановки; принятие решения; проведение рекогносцировки; отдача боевого приказа; организация взаимодействия...
|
|

 , 3 весом
, 3 весом  , связанных между собой зубчатым зацеплением (рис. 4.7). К барабану 2, приводящему в движение систему, приложена пара сил, постоянный момент которой
, связанных между собой зубчатым зацеплением (рис. 4.7). К барабану 2, приводящему в движение систему, приложена пара сил, постоянный момент которой  . К барабану 3 приложена пара сил, постоянный момент сопротивления которой
. К барабану 3 приложена пара сил, постоянный момент сопротивления которой  . Груз 1 весом
. Груз 1 весом 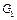 движется по шероховатой наклонной плоскости, расположенной под углом α к горизонту, при этом груз 4 весом
движется по шероховатой наклонной плоскости, расположенной под углом α к горизонту, при этом груз 4 весом  перемещается по вертикали. Коэффициент трения груза 1 о наклонную плоскость –
перемещается по вертикали. Коэффициент трения груза 1 о наклонную плоскость –  ; радиусы ступеней барабанов 2, 3 соответственно –
; радиусы ступеней барабанов 2, 3 соответственно – 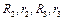 ; радиусы инерции относительно осей вращения –
; радиусы инерции относительно осей вращения –  . Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми.
. Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, – нерастяжимыми и невесомыми.
 , м
, м
 , м
, м
 , м
, м
 , м
, м
 , м
, м
 , м
, м
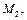



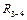




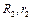 ; радиус инерции его относительно оси вращения –
; радиус инерции его относительно оси вращения – 

 ; радиусы ступеней шкивов 2, 3 –
; радиусы ступеней шкивов 2, 3 –  ; радиусы инерции их относительно осей вращения –
; радиусы инерции их относительно осей вращения – 



