Исследование движения механической системы с одной степенью свободы при помощи уравнения Лагранжа 2-го родаПример 10. Механическая система состоит из грузов 1, 4 и ступенчатых шкивов 2, 3 с неподвижными осями (рис. 3.15). К шкиву 2 приложена пара сил, момент которой Определить ускорение груза 1 и силу натяжения троса, соединяющего груз 1 со шкивом 2 в зависимости от параметра
|
, а к шкиву 3 – пара сил сопротивления, момент которой 
. Груз 1 весом 
Н опускается по шероховатой наклонной плоскости, составляющей с горизонтом угол 
. Груз 4 весом 
Н поднимается вертикально. Коэффициент трения скольжения груза 1 о плоскость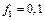 
. Веса шкивов 2, 3 одинаковы (
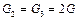). Радиусы ступеней шкивов: 
; 
; 
. Радиусы инерции шкивов относительно осей вращения 
. Все указанные элементы механической системы являются абсолютно твердыми телами и соединены между собой нерастяжимыми тросами (идеальными нитями).
.
