 В рассматриваемой механической системе груз 1 совершает поступательное движение, цилиндрический каток 2 и подвижный ступенчатый блок 4 – плоско-параллельное, неподвижный ступенчатый блок 3 – вращательное. Воспользуемся выражением для теоремы об изменении кинетической энергии в интегральной форме:
В рассматриваемой механической системе груз 1 совершает поступательное движение, цилиндрический каток 2 и подвижный ступенчатый блок 4 – плоско-параллельное, неподвижный ступенчатый блок 3 – вращательное. Воспользуемся выражением для теоремы об изменении кинетической энергии в интегральной форме:
 .
.
В этом выражении  и Т – кинетическая энергия системы в начальном и конечном положениях соответственно;
и Т – кинетическая энергия системы в начальном и конечном положениях соответственно;  – сумма работ внешних сил, приложенных к системе;
– сумма работ внешних сил, приложенных к системе; 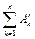 – сумма работ ее внутренних сил. Так как в начальном положении система находилась в покое, то
– сумма работ ее внутренних сил. Так как в начальном положении система находилась в покое, то  . Система состоит из абсолютно твердых тел, которые соединены нерастяжимыми тросами, поэтому
. Система состоит из абсолютно твердых тел, которые соединены нерастяжимыми тросами, поэтому 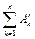 = 0 и, следовательно, кинетическая энергия
= 0 и, следовательно, кинетическая энергия  . В конечном положении она складывается из суммы кинетических энергий тел 1-4, входящих в систему
. В конечном положении она складывается из суммы кинетических энергий тел 1-4, входящих в систему
 .
.
Теперь изобразим рассматриваемую механическую систему в начальном и конечном положениях, а также все силовые факторы, действующие на эту систему (рис. 3.12). Определим кинетические энергии входящих в систему тел, выразив их через скорость  груза 1.
груза 1.
Кинетическая энергия груза 1
 .
.
Кинетическая энергия катка 2
 ,
,
где  – момент инерции катка (однородного цилиндра) относительно его продольной центральной оси,
– момент инерции катка (однородного цилиндра) относительно его продольной центральной оси,  ,
,  – угловая скорость катка, который катится без скольжения по наклонной плоскости. Его мгновенный центр скоростей находится в точке
– угловая скорость катка, который катится без скольжения по наклонной плоскости. Его мгновенный центр скоростей находится в точке  , поэтому
, поэтому  , где
, где  , откуда
, откуда  . Подставляя это отношение в формулу для кинетической энергии, получим
. Подставляя это отношение в формулу для кинетической энергии, получим
 .
.
 Кинетическая энергия неподвижного ступенчатого блока 3
Кинетическая энергия неподвижного ступенчатого блока 3
 ,
,
где  – момент инерции блока относительно его продольной центральной оси,
– момент инерции блока относительно его продольной центральной оси,  ;
;  – его угловая скорость,
– его угловая скорость,  . Так как
. Так как 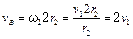 , то
, то  . Подставляя это отношение в формулу для кинетической энергии, окончательно получим
. Подставляя это отношение в формулу для кинетической энергии, окончательно получим
 .
.
Кинетическая энергия подвижного ступенчатого блока 4
 ,
,
где  – момент инерции блока относительно его продольной центральной оси,
– момент инерции блока относительно его продольной центральной оси,  ;
;  – угловая скорость блока,
– угловая скорость блока,  . Так как трос не скользит по блоку 4, его мгновенный центр скоростей находится в точке
. Так как трос не скользит по блоку 4, его мгновенный центр скоростей находится в точке  и
и  , то
, то  и
и  . Подставляя эти выражения в формулу для кинетической энергии, получим
. Подставляя эти выражения в формулу для кинетической энергии, получим
 .
.
Теперь определим кинетическую энергию всей механической системы, используя исходные данные,

 .
.
Работу в рассматриваемой системе совершают только внешние силы, изображенные в ее конечном положении (см. рис. 3.12). Определим работу внешних сил на заданных перемещениях точек системы при перемещении груза 1 на расстояние  . Работы сил
. Работы сил  и
и  равны нулю, так как точки приложения этих сил неподвижны. Работы сил
равны нулю, так как точки приложения этих сил неподвижны. Работы сил 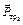 и
и  равны нулю, так как эти силы приложены в точках, которые являются мгновенными центрами скоростей. Реакция
равны нулю, так как эти силы приложены в точках, которые являются мгновенными центрами скоростей. Реакция  перпендикулярна перемещению груза 1 и ее работа также равна нулю. Запишем формулу для нахождения суммы работ оставшихся внешних сил
перпендикулярна перемещению груза 1 и ее работа также равна нулю. Запишем формулу для нахождения суммы работ оставшихся внешних сил

и определим составляющие, входящие в эту сумму:
– работу силы тяжести 
 ;
;
– работу силы трения скольжения
 ,
,
где  , а значит
, а значит
 ;
;
– работу силы тяжести  с учетом того, что
с учетом того, что  ,
,
 ;
;
– работу пары сил сопротивления качению катка 2, момент которой  ,
,
 ,
,
где  , а угол поворота катка 2, катящегося без скольжения,
, а угол поворота катка 2, катящегося без скольжения,  , откуда следует, что
, откуда следует, что
 ;
;
– работу силы тяжести 
 .
.
При нахождении слагаемых  и
и  следовало учесть, что зависимость между линейными и угловыми скоростями такая же, как между соответствующими линейными и угловыми перемещениями.
следовало учесть, что зависимость между линейными и угловыми скоростями такая же, как между соответствующими линейными и угловыми перемещениями.
Теперь определим сумму работ внешних сил, пользуя исходные данные:

 .
.
Согласно выражению для теоремы об изменении кинетической энергии, приравнивая значения Т и  , сократив на m обе части этого равенства, получим значение скорости груза 1 из формулы
, сократив на m обе части этого равенства, получим значение скорости груза 1 из формулы  , откуда
, откуда
 м/с.
м/с.
Пример 9. Механическая система, показанная на рис. 3.13, состоит из грузов 1, 4, блока 2 с неподвижной осью вращения и ступенчатого цилиндрического катка 3. Груз 1 массой  = 8 m опускается вертикально и с помощью нерастяжимого троса, переброшенного через блок 2 (однородный цилиндр), приводит в движение каток 3. Он, в свою очередь, связан с помощью того же троса, прикрепленного в центре масс, с грузом 4, поднимающимся, как и каток 2, по шероховатой наклонной плоскости, которая составляет с горизонтом угол
= 8 m опускается вертикально и с помощью нерастяжимого троса, переброшенного через блок 2 (однородный цилиндр), приводит в движение каток 3. Он, в свою очередь, связан с помощью того же троса, прикрепленного в центре масс, с грузом 4, поднимающимся, как и каток 2, по шероховатой наклонной плоскости, которая составляет с горизонтом угол  . Коэффициент трения груза 4 о плоскость
. Коэффициент трения груза 4 о плоскость  , его масса
, его масса 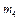 = m; масса блока 2
= m; масса блока 2  = 5 m; масса катка 3
= 5 m; масса катка 3  = 2 m; радиусы ступеней катка 3:
= 2 m; радиусы ступеней катка 3:  = 0, 3 м,
= 0, 3 м,  = 0, 1 м, его радиус инерции
= 0, 1 м, его радиус инерции  = 0, 2 м.
= 0, 2 м.
 Определить скорость центра масс
Определить скорость центра масс  и угловую скорость
и угловую скорость  катка 3 после того, как груз 1 опустится на расстояние
катка 3 после того, как груз 1 опустится на расстояние  = 1 м при условии, что трением качения катка 3 по наклонной плоскости можно пренебречь.
= 1 м при условии, что трением качения катка 3 по наклонной плоскости можно пренебречь.

 В рассматриваемой механической системе груз 1 совершает поступательное движение, цилиндрический каток 2 и подвижный ступенчатый блок 4 – плоско-параллельное, неподвижный ступенчатый блок 3 – вращательное. Воспользуемся выражением для теоремы об изменении кинетической энергии в интегральной форме:
В рассматриваемой механической системе груз 1 совершает поступательное движение, цилиндрический каток 2 и подвижный ступенчатый блок 4 – плоско-параллельное, неподвижный ступенчатый блок 3 – вращательное. Воспользуемся выражением для теоремы об изменении кинетической энергии в интегральной форме: .
. и Т – кинетическая энергия системы в начальном и конечном положениях соответственно;
и Т – кинетическая энергия системы в начальном и конечном положениях соответственно;  – сумма работ внешних сил, приложенных к системе;
– сумма работ внешних сил, приложенных к системе; 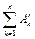 – сумма работ ее внутренних сил. Так как в начальном положении система находилась в покое, то
– сумма работ ее внутренних сил. Так как в начальном положении система находилась в покое, то  . Система состоит из абсолютно твердых тел, которые соединены нерастяжимыми тросами, поэтому
. Система состоит из абсолютно твердых тел, которые соединены нерастяжимыми тросами, поэтому  . В конечном положении она складывается из суммы кинетических энергий тел 1-4, входящих в систему
. В конечном положении она складывается из суммы кинетических энергий тел 1-4, входящих в систему .
. груза 1.
груза 1. .
. ,
, – момент инерции катка (однородного цилиндра) относительно его продольной центральной оси,
– момент инерции катка (однородного цилиндра) относительно его продольной центральной оси,  ,
,  – угловая скорость катка, который катится без скольжения по наклонной плоскости. Его мгновенный центр скоростей находится в точке
– угловая скорость катка, который катится без скольжения по наклонной плоскости. Его мгновенный центр скоростей находится в точке  , поэтому
, поэтому  , где
, где  , откуда
, откуда  . Подставляя это отношение в формулу для кинетической энергии, получим
. Подставляя это отношение в формулу для кинетической энергии, получим .
. Кинетическая энергия неподвижного ступенчатого блока 3
Кинетическая энергия неподвижного ступенчатого блока 3 ,
, – момент инерции блока относительно его продольной центральной оси,
– момент инерции блока относительно его продольной центральной оси,  ;
;  – его угловая скорость,
– его угловая скорость,  . Так как
. Так как 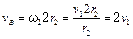 , то
, то  . Подставляя это отношение в формулу для кинетической энергии, окончательно получим
. Подставляя это отношение в формулу для кинетической энергии, окончательно получим .
. ,
, – момент инерции блока относительно его продольной центральной оси,
– момент инерции блока относительно его продольной центральной оси,  ;
;  – угловая скорость блока,
– угловая скорость блока,  . Так как трос не скользит по блоку 4, его мгновенный центр скоростей находится в точке
. Так как трос не скользит по блоку 4, его мгновенный центр скоростей находится в точке  и
и  , то
, то  и
и  . Подставляя эти выражения в формулу для кинетической энергии, получим
. Подставляя эти выражения в формулу для кинетической энергии, получим .
.
 .
. . Работы сил
. Работы сил  и
и  равны нулю, так как точки приложения этих сил неподвижны. Работы сил
равны нулю, так как точки приложения этих сил неподвижны. Работы сил 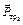 и
и  равны нулю, так как эти силы приложены в точках, которые являются мгновенными центрами скоростей. Реакция
равны нулю, так как эти силы приложены в точках, которые являются мгновенными центрами скоростей. Реакция  перпендикулярна перемещению груза 1 и ее работа также равна нулю. Запишем формулу для нахождения суммы работ оставшихся внешних сил
перпендикулярна перемещению груза 1 и ее работа также равна нулю. Запишем формулу для нахождения суммы работ оставшихся внешних сил

 ;
; ,
, , а значит
, а значит ;
; с учетом того, что
с учетом того, что  ,
, ;
; ,
, ,
, , а угол поворота катка 2, катящегося без скольжения,
, а угол поворота катка 2, катящегося без скольжения,  , откуда следует, что
, откуда следует, что ;
;
 .
. и
и  следовало учесть, что зависимость между линейными и угловыми скоростями такая же, как между соответствующими линейными и угловыми перемещениями.
следовало учесть, что зависимость между линейными и угловыми скоростями такая же, как между соответствующими линейными и угловыми перемещениями.
 .
. , сократив на m обе части этого равенства, получим значение скорости груза 1 из формулы
, сократив на m обе части этого равенства, получим значение скорости груза 1 из формулы  , откуда
, откуда м/с.
м/с. = 8 m опускается вертикально и с помощью нерастяжимого троса, переброшенного через блок 2 (однородный цилиндр), приводит в движение каток 3. Он, в свою очередь, связан с помощью того же троса, прикрепленного в центре масс, с грузом 4, поднимающимся, как и каток 2, по шероховатой наклонной плоскости, которая составляет с горизонтом угол
= 8 m опускается вертикально и с помощью нерастяжимого троса, переброшенного через блок 2 (однородный цилиндр), приводит в движение каток 3. Он, в свою очередь, связан с помощью того же троса, прикрепленного в центре масс, с грузом 4, поднимающимся, как и каток 2, по шероховатой наклонной плоскости, которая составляет с горизонтом угол  . Коэффициент трения груза 4 о плоскость
. Коэффициент трения груза 4 о плоскость  , его масса
, его масса 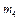 = m; масса блока 2
= m; масса блока 2  = 5 m; масса катка 3
= 5 m; масса катка 3  = 2 m; радиусы ступеней катка 3:
= 2 m; радиусы ступеней катка 3:  = 0, 3 м,
= 0, 3 м,  = 0, 1 м, его радиус инерции
= 0, 1 м, его радиус инерции  = 0, 2 м.
= 0, 2 м. Определить скорость центра масс
Определить скорость центра масс  и угловую скорость
и угловую скорость  катка 3 после того, как груз 1 опустится на расстояние
катка 3 после того, как груз 1 опустится на расстояние 


