И правила определения их реакций
1. Свободное опирание тела о связь (тело изображено в виде бруска, а связь заштрихована, рис. 1.7).
Рис. 1.7. Реакции при свободном опирании тел
2. Гибкая связь (рис. 1.8). Реакции нитей или цепей всегда направлены вдоль самих связей в сторону от тела к связи.
Рис. 1.8. Реакции гибких нитей
3. Стержневая связь (рис. 1.9). Реакции стержневых связей направлены вдоль прямой, проходящей через оси концевых шарниров.
Рис. 1.9. Реакции при шарнирном закреплении стержня
4. Шарнирно-подвижная опора (рис. 1.10). Такая опора представляет собой видоизменение свободного опирания.

Рис. 1.10. Шарнирно-подвижная опора: а – схемы и направление реакций; б – условные изображения 5. Шарнирно-неподвижная опора (рис. 1.11). Такая опора дает возможность телу свободно поворачиваться около шарнира, но препятствует поступательному перемещению тела в любом направлении, перпендикулярном оси шарнира.
Рис. 1.11. Шарнирно-неподвижная опора. Условное изображение и направление реакций
6. Глухая заделка (жесткое защемление) (рис. 1.12). Такая заделка исключает любое перемещение тела.
а б
Рис. 1.12. Глухая заделка: а – условное изображение; б – направление реакции
Глава 2. Плоская система сходящихся сил
2.1. Сложение плоской системы сходящихся сил. Геометрическое условие равновесия
Система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке, называется плоской системой сходящихся сил. Если силы сходящейся системы приложены к разным точкам тела, то по первому следствию из аксиом статики каждую силу можно перенести в точку пересечения линий действия и получить эквивалентную систему сил, приложенных к одной точке (рис. 2.1).
Рис. 2.1. Плоская система сходящихся сил
Две силы, приложенные к одной точке тела, образуют простейшую плоскую систему сходящихся сил (две пересекающиеся прямые всегда лежат в одной плоскости). Рассмотрим систему сил Применив правило силового треугольника, сложим силы
Рис. 2.2. Многоугольник сил
Теперь сложим силу
где Порядок построения сторон силового многоугольника не влияет на окончательный результат. Чтобы уравновесить систему сил, достаточно к ней добавить еще одну силу, численно равную равнодействующей, но направленную в противоположную сторону (рис. 2.3).
Рис. 2.3. Равнодействующая системы сил Необходимое и достаточное условие равновесия системы сходящихся сил в геометрической форме: система сходящихся сил уравновешена тогда и только тогда, когда силовой многоугольник замкнут.
2.2. Определение равнодействующей системы сходящихся сил методом проекций. Аналитическое условие равновесия Вместо построения силового многоугольника равнодействующую системы сходящихся сил более точно и значительно быстрее находят вычислением с помощью метода проекций, который обычно называется аналитическим. Проекцией вектора
Рис. 2.4. Проекции векторов сил на оси
Рассмотрим определение равнодействующей системы сходящихся сил методом проекций. Допустим, что для заданной системы сходящихся сил построен многоугольник ABCDE, в котором вектор
Рис. 2.5. Многоугольник сил
Выбрав систему координатных осей X и Y в плоскости силового многоугольника, спроецируем его на эти оси:
В краткой форме эти равенства записываются так:
где Таким образом, проекция равнодействующей системы сходящихся сил на каждую из осей координат равна алгебраической сумме проекций составляющих сил на ту же ось:
Условие равновесия плоской системы сходящихся сил в аналитической форме: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил системы на каждую из двух осей координат были равны нулю.
Глава 3. Теория пар сил на плоскости 3.1. Пара сил. Эквивалентность пар сил
Система двух параллельных сил, равных по модулю и направленных в противоположные стороны, называется парой сил или просто парой (рис. 3.1). Понятие о паре сил ввел в механику французский ученый Луи Пуансон (1777–1859).
Рис. 3.1. Пара сил
Пара сил – неуравновешенная система и не имеет равнодействующей. Пара сил производит на тело вращательное действие. Вращательный эффект пары измеряется взятым со знаком «плюс» или «минус» произведением модуля одной из сил пары на ее плечо (момент пары):
Знак «плюс» ставится перед числовым значением момента в том случае, если пара стремится повернуть тело против хода часовой стрелки, и знак «минус» – если пара стремится повернуть тело по ходу часовой стрелки (рис. 3.2).
Рис. 3.2. Правило знаков момента пары сил
В Международной системе единиц (СИ) моменты пар выражаются в Вращательное действие расположенной в данной плоскости пары зависит только от ее момента, поэтому для задания пары сил достаточно указать числовое значение ее момента, а затем по данному или выбранному плечу определить силы пары или по силам подобрать необходимое плечо. Исходя из этого, на рисунках и схемах пары сил изображают иногда просто круговой стрелкой, характеризующей лишь направление вращающего действия. Например, пары (
б
Рис. 3.3. Изображение пары сил
3.2. Сложение пар сил. Условие равновесия пар
Теорема: Система пар сил, действующих на тело в одной плоскости, эквивалентна паре сил с моментом, равным алгебраической сумме моментов пар системы. Допустим, на тело действуют три пары, моменты которых M 1, M 2 и M 3 известны (рис. 3.4).
Рис. 3.4. Система пар сил Момент равнодействующей пары
Если в результате сложения пар
т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю. Значит, систему пар или одну пару можно уравновесить только парой.
3.3. Момент пары относительно точки
Задолго до появления понятия о паре сил и ее моменте в механике возникло понятие о моменте силы относительно точки. Первый, кто обратил внимание на важную роль в механике момента силы относительно точки, был Леонардо да Винчи (1452–1519), современную трактовку понятия момента силы относительно точки дал П. Вариньон (1654–1722). Моментом силы относительно точки называется взятое со знаком «плюс» или «минус» произведение модуля силы на кратчайшее расстояние от точки до линии действия силы:
Точка О, относительно которой берется момент силы, называется центром момента. OВ = l – кратчайшее расстояние от центра момента до линии действия силы – называется плечом силы относительно данной точки. Знак «плюс» ставится в случае, если сила F стремится повернуть тело против хода часовой стрелки, а знак «минус» – в противоположном случае (правило знаков то же, что и у моментов пар сил). Момент силы относительно точки О на рис. 3.5 положительный.
Рис. 3.5. Момент силы относительно точки
Глава 4. Плоская система произвольно расположенных сил (ПСПРС)
4.1. Приведение силы к точке
Теорема о параллельном переносе силы в любую заданную или выбранную точку. Пусть дана сила
Рис. 4.1. Параллельный перенос силы
Таким образом, всякую силу Операция такого переноса силы называется приведением силы к точке, а появляющаяся при этом пара Операция приведения силы к точке имеет глубокий физический смысл.
4.2. Приведение к точке плоской системы произвольно расположенных сил
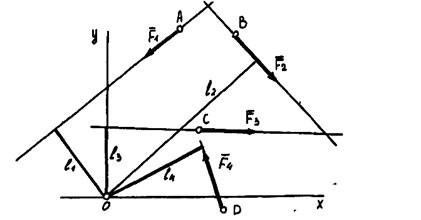
Пусть задана система четырех сил Выберем произвольную точку O – центр приведения – и приведем к нему силу
Рис. 4.2. Плоская система произвольно расположенных сил
Рис. 4.3. Приведение системы сил к центру
Затем приведем к точке O силу С помощью силового многоугольника находим силу
или, так как моменты присоединенных пар равны моментам данных сил относительно центра приведения:
Главный вектор системы Главный момент системы Произвольная плоская система сил эквивалентна одной силе – главному вектору – и одной паре, момент которой равен главному моменту. Допустим, что, приведя плоскую систему сил к точке, мы получили главный вектор
Рис. 4.4. Главный вектор и главный момент сил Представим главный момент в виде пары сил (
Рис. 4.5
Тогда силы
Рис. 4.6. Равнодействующая системы сил Расстояние от центра приведения до линии действия равнодействующей:
Следовательно, равнодействующая ПСПРС равна главному вектору и расстояние от центра приведения до линии действия равнодействующей равно частному от деления главного момента на модуль главного вектора или равнодействующей.
4.3. Теорема Вариньона
Непосредственно из равенства
Из рис. 4.6 следует, что
т. е. момент равнодействующей ПСПРС относительно любой точки равен алгебраической сумме моментов сил системы, взятых относительно той же точки.
4.4. Уравнения равновесия и их различные формы
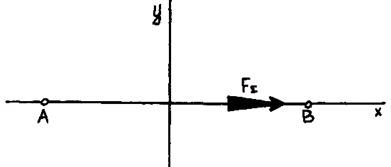
Первая форма уравнений равновесия. Если плоская система сил уравновешена, то алгебраические суммы проекций всех сил на оси X и Y равны нулю, а также равна нулю алгебраическая сумма моментов всех сил относительно любой точки:
Уравнений равновесия три, т. е. в произвольной плоской уравновешенной системе число неизвестных сил не должно превышать трех. Вторая форма уравнений равновесия (рис. 4.7).
Рис. 4.7. Вторая форма уравнений равновесия
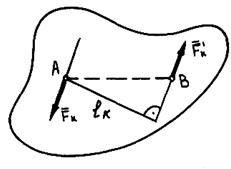
Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно двух любых точек, а также алгебраическая сумма проекций сил на ось, не перпендикулярную прямой, проходящей через эти точки, равны нулю:
Третья форма уравнений равновесия. Если произвольная плоская система сил уравновешена, то алгебраические суммы моментов сил относительно любых трех точек, не лежащих на одной прямой, равны нулю:
|








 , приложенных в точке А. Требуется найти их равнодействующую (рис. 2.2).
, приложенных в точке А. Требуется найти их равнодействующую (рис. 2.2). и
и  . Для этого из конца вектора
. Для этого из конца вектора  отложим вектор
отложим вектор  и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил
и, соединив точки А и С, получим геометрическую сумму (равнодействующую) сил 


 с силой
с силой  . Для этого из конца вектора ВС =
. Для этого из конца вектора ВС =  и, соединив точки А и D, получим равнодействующую трех сил:
и, соединив точки А и D, получим равнодействующую трех сил:
 – искомая равнодействующая.
– искомая равнодействующая.

 на ось называется длина направленного отрезка оси, заключенного между двумя перпендикулярами, опущенными из начала и конца вектора
на ось называется длина направленного отрезка оси, заключенного между двумя перпендикулярами, опущенными из начала и конца вектора  . Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси (рис. 2.4):
. Проекция силы на ось равна произведению модуля этой силы на косинус угла между направлением силы и положительным направлением оси (рис. 2.4):

 – искомая равнодействующая данной системы.
– искомая равнодействующая данной системы.


 – знак суммы, а индекс k последовательно принимает значения от 1 до n, по числу сходящихся сил, равнодействующая которых определяется.
– знак суммы, а индекс k последовательно принимает значения от 1 до n, по числу сходящихся сил, равнодействующая которых определяется. .
.
 .
.

 или
или  .
. ) и (
) и ( ) (рис. 3.3, а), приложенные к брусу, можно условно изобразить круговыми стрелками, обозначив их M 1 и M 2 (рис. 3.3, б).
) (рис. 3.3, а), приложенные к брусу, можно условно изобразить круговыми стрелками, обозначив их M 1 и M 2 (рис. 3.3, б).

 а
а

 ,
,
 , то действующие на тело пары сил образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением:
, то действующие на тело пары сил образуют уравновешенную систему. Следовательно, необходимое и достаточное условие равновесия системы пар выражается одним уравнением: ,
,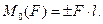
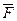 , приложенная к точке А твердого тела (рис. 4.1, а), и ее требуется перенести в точку О. Приложим к телу в точке О уравновешенную систему сил
, приложенная к точке А твердого тела (рис. 4.1, а), и ее требуется перенести в точку О. Приложим к телу в точке О уравновешенную систему сил  , параллельных
, параллельных  , рис. 4.1, б). Теперь кроме силы
, рис. 4.1, б). Теперь кроме силы  , приложенной к точке О, образовались пара сил
, приложенной к точке О, образовались пара сил  с моментом
с моментом  и момент данной силы
и момент данной силы  , т. е.
, т. е.  (рис. 4.1, в).
(рис. 4.1, в).


 с моментом
с моментом  – присоединенной парой.
– присоединенной парой. и
и  (рис. 4.2).
(рис. 4.2). (на рисунке присоединенные моменты изображены круговыми стрелками, направленными в сторону поворота силами
(на рисунке присоединенные моменты изображены круговыми стрелками, направленными в сторону поворота силами  ).
).

 . Перенесем ее в эту точку и присоединим пару с моментом
. Перенесем ее в эту точку и присоединим пару с моментом  . Так же поступим с остальными силами
. Так же поступим с остальными силами  и
и 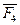 , присоединив пары с моментами
, присоединив пары с моментами  и
и  . Как видно из рис. 4.3, в результате последовательного приведения заданных сил к точке образовалась система сходящихся сил и система присоединенных пар с моментами, равными моментам заданных сил относительно точки (центра) приведения.
. Как видно из рис. 4.3, в результате последовательного приведения заданных сил к точке образовалась система сходящихся сил и система присоединенных пар с моментами, равными моментам заданных сил относительно точки (центра) приведения. , эквивалентную системе приведенных сил. Сложив алгебраические моменты присоединенных пар, найдем момент одной эквивалентной им пары:
, эквивалентную системе приведенных сил. Сложив алгебраические моменты присоединенных пар, найдем момент одной эквивалентной им пары:

 .
.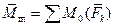 .
. и пару сил с моментом
и пару сил с моментом  (рис. 4.4).
(рис. 4.4).
 ), численно равных главному вектору (
), численно равных главному вектору ( ), с плечом
), с плечом 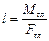 . Расположим эту пару таким образом, чтобы одна из сил оказалась направленной вдоль линии действия главного вектора, но в противоположную сторону (рис. 4.5).
. Расположим эту пару таким образом, чтобы одна из сил оказалась направленной вдоль линии действия главного вектора, но в противоположную сторону (рис. 4.5).
 и
и  и есть искомая равнодействующая рассматриваемой системы сил (рис. 4.6).
и есть искомая равнодействующая рассматриваемой системы сил (рис. 4.6).

 вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем предыдущее равенство в таком виде:
вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем предыдущее равенство в таком виде:
 – момент равнодействующей относительно любой точки, а по формуле
– момент равнодействующей относительно любой точки, а по формуле  , поэтому последнее равенство можно переписать в виде
, поэтому последнее равенство можно переписать в виде ,
,