Масштабные коэффициенты
Масштабным коэффициентом называется отношение численного значения физической величины к длине отрезка в миллиметрах, изображающего эту величину. Например, если длина звена равна l = 0, 05 м, а отрезок, изображающий это звено, AB = 50 мм, то масштабный коэффициент длин μ 1 = 0, 05/50 = 0, 001 м/мм, что соответствует чертежному масштабу 1: 1; если же АВ = 25 мм, то μ 1= 0, 05/25 = 0, 002 м/мм (1: 2). Масштабный коэффициент скоростей μ υ ,
14.2. Построение положений рычажных механизмов методом засечек
Кинематический анализ механизмов выполняется в порядке присоединения структурных групп. Построение положений плоских механизмов второго класса обычно выполняется методом засечек. В качестве примера рассмотрим кривошипно-ползунный механизм (рис.14.1).
Рис. 14.1. Кривошипно-ползунный механизм
Вначале находим крайние положения механизма (0 и 3), в которых кривошип 1 и шатун 2 располагаются на одной прямой. Для этого из центра О делаем засечки радиусами АВ + ОА и АB – ОА на линии движения ползуна 3. Далее делим окружность, описываемую точкой А, на равные части (например, на шесть) и отмечаем последовательные положения точки А – 0, 1, 2, 3, 4, 5, 6, а затем методом засечек на линии движения ползуна получаем последовательные положения точки В – 0, 1, 2, 3 (движение справа налево) 4, 5, 6 (движение слева направо). S – ход ползуна. В результате получаем последовательные положения всех звеньев механизма. Траектория некоторой точки К шатуна получается, если все последовательные положения точки соединить плавной кривой.
14.3. Определение скоростей и ускорений рычажных механизмов методом планов
Пример 14.1. Дано: кривошипно-ползунный механизм (рис. 14.2), Формула строения:
а б в
Рис. 14.2. К примеру 14.1
Построение плана скоростей. Скорость точки А начального звена
где
Рассматриваем структурную группу (2, 3). Для определения скорости точки B составляем векторное уравнение согласно теореме о плоскопараллельном движении:
где Уравнение (14.1) решаем графически. Для этого из полюса p откладываем отрезок pa в направлении вектора
Для определения направления угловой скорости Скорость точки K шатуна находим на основании векторных уравнений
где
Отметим основные свойства планов скоростей. 1. Векторы абсолютных скоростей начинаются в полюсе плана. 2. Векторы относительных скоростей соединяют концы векторов абсолютных скоростей, причем вектор на плане направлен к той точке, которая стоит первой в индексе, например, 3. Теорема подобия. Отрезки относительных скоростей точек, принадлежащих одному звену, образуют фигуру, подобную соответствующей фигуре звена и сходственно с нею расположенную. Сходственное расположение означает, что направления обхода одноименных контуров совпадают (например, а-b-k и А-В-K – по часовой стрелке). В рассмотренном примере Построение плана ускорений. Ускорение точки А начального звена
где
причем вектор Выбираем масштабный коэффициент ускорений
Рассматриваем структурную группу (2, 3). Для определения ускорения точки В составляем векторное уравнение согласно теореме о плоскопараллельном движении:
где
Отрезок, изображающий
Уравнение (14.2) решаем графически. Для этого из точки a откладываем отрезок
Для определения направления углового ускорения Ускорение точки K находим на основании теоремы подобия, которая справедлива и для плана ускорений. Для этого методом засечек строим
откуда
В результате получим
Основные свойства планов ускорений такие же, как и планов скоростей.
Глава 15. Методические указания к решению задач
15.1. Кинематика зубчатых механизмов с неподвижными осями вращения
Основным кинематическим параметром зубчатого механизма является передаточное отношение. Передаточным отношением Очевидно, что
Если
где Для механизмов с параллельными осями передаточное отношение считается положительным при одинаковом направлении угловых скоростей и отрицательным – при противоположном. Для цилиндрической передачи знак «плюс» соответствует внутреннему зацеплению (рис. 15.1, б), а «минус» – внешнему (рис. 15.1, а).
Рис. 15.1. К вопросу о передаточном отношении
Передаточное отношение можно представить в виде
Многоступенчатый зубчатый механизм можно образовать последовательным соединением колес (рис. 15.2), при котором вращение от ведущего вала О 1 передается ведомому валу О 4 через промежуточные валы О 2 и O 3, на каждом из которых помещено по два колеса: 2 и 2´, 3 и 3´. Колёса 2 и 2´ жестко соединены с валом O 2 и имеют общую угловую скорость На одной проекции (см. рис. 15.2) направление угловых скоростей показано круговыми стрелками, а на второй – прямыми. При последовательном ступенчатом соединении колес передаточное отношение равно произведению передаточных отношений промежуточных зацеплений (см. рис. 15.2):
В данном случае имеем трехступенчатую передачу.
Рис. 15.2. Многоступенчатый зубчатый механизм
В общем случае передаточное отношение
где k – число внешних зацеплений. При простом последовательном соединении зубчатых колес (рис. 15.3) величина общего передаточного отношения не зависит от количества промежуточных (паразитных) колес:
В общем случае
где K – число внешних зацеплений. «Паразитные» колеса могут изменять знак передаточного отношения; например, при внешнем зацеплении (см. рис. 15.3) каждое четное колесо 2 и 4 вращается в сторону, противоположную вращению входного колеса 1, а каждое нечетное колесо 3 – в сторону вращения входного колеса 1.
Рис. 15.3. Последовательное соединение зубчатых колес
На рис. 15.4 показано последовательное соединение, состоящее из трех колес: 1, «паразитное» 2 и выходное 3 с внутренним зацеплением. Передаточное отношение
Рис. 15.4. Последовательное соединение трех колес
Передаточное отношение червячной передачи равно отношению числа зубьев колеса к числу витков червяка:
где
Механизм, изображенный на рис. 15.5, состоит из пары цилиндрических колес 1 и 2, пары конических колес 2´, 3 и червячной пары 3´ и 4, где звено 3´ – червяк, а 4 – червячное колесо. Общее передаточное отношение для этого механизма
где
Знак для общего передаточного отношения можно поставить лишь для того случая, когда входной и выходной валы вращаются относительно осей, параллельных друг другу.
Рис. 15.5. Многоступенчатый механизм
15.2. Кинематика зубчатых механизмов с подвижными осями вращения
Зубчатая передача, у которой геометрическая ось хотя бы одного из колес подвижна, называется планетарной. Различные планетарные механизмы можно представить в виде трех типов передач. 1. Дифференциальные передачи, обладающие двумя степенями подвижности, у которых все основные звенья подвижны (рис. 15.6). Эти передачи позволяют суммировать два или несколько потоков мощности, поступающих от независимых источников, либо распределять их по независимым потребителям.
Рис. 15.6. Дифференциальная передача 2. Простые планетарные передачи, обладающие одной степенью подвижности, у которых одно из основных звеньев закреплено неподвижно (рис. 15.7, закреплено звено 3). Такие механизмы служат для последовательной передачи потока мощности.
Рис. 15.7. Планетарная передача
3. Замкнутые дифференциальные передачи, получаемые из дифференциальных передач путем замыкания двух основных звеньев (центрального колеса и водила) простой передачей, состоящей из колес 1, 2, 3 (рис. 15.8). Такие передачи позволяют получить большие передаточные отношения при малых габаритах.
Рис. 15.8. Замкнутая дифференциальная передача Рассмотрим механизм, изображенный на рис. 15.6. Определим число степеней подвижности, если n = 4 – число звеньев, p 5 = 4 и p 4 = 2 – число кинематических пар V и IV класса. Определенность в движении звеньев уэтого механизма будет в том случае, если будут заданы законы движения двум звеньям. Основными звеньями механизмов с подвижными осями являются водило (Н) и соосные с ним колёса (1 и 3). В данном случае все основные звенья подвижные. Оба эти признака (W > 1 и подвижные основные звенья) определяют дифференциальный механизм. Определим степень подвижности для механизма, изображенного на рис. 15.7:
У этого механизма колесо 3 (основное звено) неподвижно и W = 1. Оба признака определяют планетарный механизм. В механизмах замкнутых дифференциалов все основные звенья подвижные но число степеней подвижности равно единице (W = 1). Таким образом, только по совокупности двух признаков механизмы с подвижными осями можно отнести к тому или иному типу. Формулы (15.1), (15.2) для определения передаточного отношения планетарных и дифференциальных механизмов использовать нельзя, так как сателлит участвует в сложном движении, состоящем из вращения вокруг оси O 2 и вращения вместе с водилом Н вокруг оси О н (см. рис. 15.6, 15.7). Для вывода зависимостей, связывающих угловые скорости механизмов, имеющих подвижные оси, воспользуемся методом обращения движения. Допустим, что в действительном движении звенья механизма (см. рис.15.6) имеют угловые скорости
\ Так как водило Н стало неподвижным (
где
В правую часть предыдущей зависимости подставим значение относительных скоростей:
Полученное уравнение называется формулой Виллиса для дифференциальных механизмов. Левая часть, как показано выше, может быть выражена через число зубьев колес. Определенность в решении правой части будет иметь место, когда будут известны скорости двух ведущих звеньев. Установим, какой вид примет формула Виллиса для планетарного механизма, изображенного на рис. 15.7. У этого механизма колесо 3 жестко соединено со стойкой (заторможено), т. е. Таким образом, имеем
Откуда
Полученную зависимость называют формулой Виллиса для планетарных механизмов, а передаточное отношение Как и для дифференциальных механизмов,
где Достоинством планетарных механизмов является возможность получения больших передаточных отношений при малых габаритах. Пример 15.1. Определить передаточное отношение
Рис. 15.9. К примеру 15.1
Это одноступенчатый планетарный редуктор. Используя формулу (15.4), запишем
Пример 15.2. В зубчатой передаче, показанной на рис. 15.10, входное коническое колесо 1 в данный момент имеет угловую скорость
z 1 = z 2 = 18; z 2´ = z 4´ = 18; z 3 = z 5 = 30; z 3´ = z 5´ = 22; z 4 = z 6 = 70.
Рис. 15.10. К примеру 15.2
Принять средний модуль конического колеса mm = 2 мм, ширину колеса b = 20 мм, плотность ρ = 8000 кг/м, смещение центра масс (точки А, рис. 15.11) l = 2 мм.
Рис. 15.11. Смещение центра масс Определить: 1) передаточное отношение между входным и выходным звеньями и направление вращения; 2) угловую скорость и угловое ускорение выходного звена, их направление показать на схеме передачи; 3) время, в течение которого угловая скорость увеличится в два раза; 4) величину и направление силы инерции и момента пары сил инерции звена 1 в начале и конце найденного в предшествующем пункте промежутка времени, сравнить силу инерции с силой тяжести и показать на чертеже направления вращения, ускорения и инерционных нагрузок; 5) общий коэффициент полезного действия передачи.
|

 . Если скорость некоторой точки А υ A = 10 м/с, а отрезок, изображающий υ A,
. Если скорость некоторой точки А υ A = 10 м/с, а отрезок, изображающий υ A,  .
.
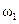 = 60 рад/с или
= 60 рад/с или  = 50 об/мин,
= 50 об/мин,  = 100 мм,
= 100 мм,  = 300 мм,
= 300 мм,  =5 рад/с2.
=5 рад/с2. механизм второго класса.
механизм второго класса.




 в сторону
в сторону  и определяем отрезок
и определяем отрезок  , мм, изображающий
, мм, изображающий  . Точка p – полюс плана скоростей.
. Точка p – полюс плана скоростей. (14.1)
(14.1) – скорость точки В во вращательном движении звена 2 относительно точки А,
– скорость точки В во вращательном движении звена 2 относительно точки А,  ,
, 
 , из точки a проводим прямую в направлении вектора
, из точки a проводим прямую в направлении вектора  , т. е. перпендикулярно AB, затем из полюса p проводим прямую в направлении суммарного вектора
, т. е. перпендикулярно AB, затем из полюса p проводим прямую в направлении суммарного вектора  , т. е. параллельно х – х. Пересечение указанных направлений дает точку b. В результате находим
, т. е. параллельно х – х. Пересечение указанных направлений дает точку b. В результате находим
 шатуна 2 переносим вектор относительной скорости
шатуна 2 переносим вектор относительной скорости  и
и 
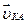 и
и  –относительные скорости, причем
–относительные скорости, причем  ,
,  .В результате получим
.В результате получим
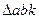 ~
~  .
.
 –нормальное ускорение;
–нормальное ускорение; – касательное (тангенциальное) ускорение.
– касательное (тангенциальное) ускорение.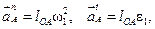
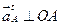 в сторону
в сторону  , и определяем отрезок
, и определяем отрезок 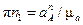 , мм, изображающий
, мм, изображающий  , и отрезок
, и отрезок  мм, изображающий
мм, изображающий  . Точка π – полюс плана ускорений. Откладываем отрезки
. Точка π – полюс плана ускорений. Откладываем отрезки  и
и 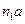 в соответствии с их направлениями. Тогда
в соответствии с их направлениями. Тогда
 (14.2)
(14.2) –нормальная и касательная составляющие ускорения
–нормальная и касательная составляющие ускорения  точки В во вращательном движении звена 2 относительно точки А, причем вектор
точки В во вращательном движении звена 2 относительно точки А, причем вектор  направлен вдоль АВ от В к А, а
направлен вдоль АВ от В к А, а  . Нормальная составляющая находится также по величине
. Нормальная составляющая находится также по величине
 равен
равен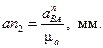
 в направлении вектора
в направлении вектора  проводим прямую в направлении вектора
проводим прямую в направлении вектора  , а из полюса π проводим прямую в направлении суммарного вектора
, а из полюса π проводим прямую в направлении суммарного вектора  , т. е. параллельно х – х. Пересечение указанных направлений дает точку b. В результате находим
, т. е. параллельно х – х. Пересечение указанных направлений дает точку b. В результате находим
 шатуна 2 переносим вектор касательного ускорения
шатуна 2 переносим вектор касательного ускорения  ) в точку В и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки А.
) в точку В и наблюдаем, в какую сторону он поворачивает звено 2 относительно точки А. и
и  находим из пропорций
находим из пропорций


 называется отношение угловой скорости звена 1 (
называется отношение угловой скорости звена 1 (
 и
и  , то
, то



 .
.

 (15.1)
(15.1)
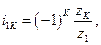 (15.2)
(15.2)



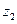 – число зубьев червячного колеса;
– число зубьев червячного колеса; –число витков червяка;
–число витков червяка;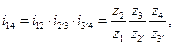
 – число зубьев червячного колеса;
– число зубьев червячного колеса;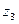 – число витков червяка.
– число витков червяка.




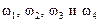 . Сообщим всем звеньям скорость, равную угловой скорости водила, но противоположно ей направленную, т. е.
. Сообщим всем звеньям скорость, равную угловой скорости водила, но противоположно ей направленную, т. е.  . В этом случае угловые скорости звеньев соответственно будут
. В этом случае угловые скорости звеньев соответственно будут
 ), то мы получили «обращенный механизм» с неподвижными осями. Для этого механизма справедлива зависимость
), то мы получили «обращенный механизм» с неподвижными осями. Для этого механизма справедлива зависимость
 –передаточное отношение «обращенного механизма», которое можно определить через число зубьев колес:
–передаточное отношение «обращенного механизма», которое можно определить через число зубьев колес:
 (15.3)
(15.3) .
.
 (15.4)
(15.4) – планетарным передаточным отношением.
– планетарным передаточным отношением. ,
,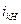 – передаточное отношение от звена k к звену l (l соответствует неподвижному центральному колесу).
– передаточное отношение от звена k к звену l (l соответствует неподвижному центральному колесу). планетарного механизма (рис. 15.9), если z 1 = 100, z 2 = 99, z 2´ = 100, z 3´ = 101.
планетарного механизма (рис. 15.9), если z 1 = 100, z 2 = 99, z 2´ = 100, z 3´ = 101.






