Кинематические цепи
Кинематической цепью называется система звеньев, связанных между собой кинематическими парами (рис. 12.1, 12.2).
12.3. Структурный синтез и анализ механизмов
Структурный синтез механизма заключается в проектировании его структурной схемы, под которой понимается схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение. Метод структурного синтеза механизмов, предложенный русским ученым Л.В. Ассуром в 1914 г., состоит в следующем: механизм может быть образован путем наслоения структурных групп к одному или нескольким начальным звеньям и стойке. Структурной группой (группой Ассура) называется кинематическая цепь, число степеней свободы которой равно нулю после присоединения ее внешними кинематическими парами к стойке и которая не распадается на более простые цепи, удовлетворяющие этому условию. Принцип наслоения иллюстрируется на примере образования Для структурных групп плоских механизмов с низшими парами
откуда
где W –число степеней свободы; n – число подвижных звеньев; Р н – число низших пар. Этому соотношению удовлетворяют следующие сочетания.
В роли одноподвижных пар выступают низшие пары. Простейшей является структурная группа, у которой n = 2 и P н = 3. Она называется структурной группой второго класса.
а б в г
Рис. 12.3. Принцип наслоения структур, φ 1 –угол поворота кривошипа (обобщенная координата)
Порядок структурной группы определяется числом элементов ее внешних кинематических пар, которыми она может присоединяться к механизму. Все группы второго класса имеют второй порядок. Структурные группы, у которых n = 4 и Р н = 6, могут быть третьего или четвертого класса (рис. 12.4).
а б Рис. 12.4. Структурные группы: а – третьего класса; б – четвертого класса Класс структурной группы в общем случае определяется числом кинематических пар в замкнутом контуре, образованном внутренними кинематическими парами. Класс механизма определяется высшим классом структурной группы, входящей в его состав. Порядок образования механизма записывается в виде формулы его строения. Для рассмотренного примера (см. рис. 12.3): (0, 1) →
12.4. Конструктивно-функциональная классификация механизмов
Согласно этой классификации механизмы можно разделить на пять основных видов: рычажные, кулачковые, фрикционные, зубчатые механизмы и механизмы с гибкими звеньями. К рычажным механизмам относятся механизмы, звенья которых образуют только вращательные, поступательные, цилиндрические и сферические пары. На рис. 12.5 показаны схемы наиболее распространенных рычажных механизмов: кривошипно-ползунного (рис. 12.5, а), шарнирного четырехзвенника (рис. 12.5, б), кулисного (рис. 12.5, в). Кривошип – вращающееся звено, которое может совершать полный оборот вокруг неподвижной оси (звено 1 на всех трех схемах рис. 12.5). Шатун – звено, которое образует кинематические пары только с подвижными звеньями (звено 2 на рис. 12.5, а, б). Ползун – звено, образующее поступательную пару со стойкой (звено 3 на рис. 12.5, а и звено 2 на рис. 12.5, в). Коромысло – вращающееся звено, которое может совершать только неполный оборот вокруг неподвижной оси (звено 3 на рис. 12.5, б). Кулиса – звено, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару (звено 3 на рис. 12.5, в).
а б в Рис. 12.5. Рычажные механизмы
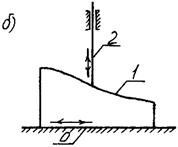
К кулачковым механизмам относятся механизмы, в состав которых входит кулачок – звено, имеющее элемент высшей пары, выполненный в виде поверхности переменной кривизны. Кулачковые механизмы (рис. 12.6) предназначены для преобразования вращательного или возвратно-поступательного движения входного эвена, которым, как правило, является кулачок 1, в возвратно-поступательное или возвратно-вращательное движение выходного звена-толкателя 2.
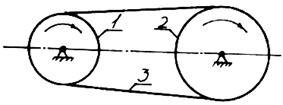
Рис. 12.6. Кулачковые механизмы Основное достоинство кулачковых механизмов заключается в возможности получения практически любого закона движения толкателя за счет соответствующего выбора профиля кулачка. Во фрикционных механизмах (рис. 12.7) движение от входного звена к выходному передается за счет сил трения, возникающих в местах контакта звеньев (высшая пара).
Рис. 12.7. Фрикционный механизм
К зубчатым механизмам относятся механизмы, в состав которых входят зубчатые звенья. Механизмы с гибкими связями (рис. 12.8) применяют для передачи вращательного движения между валами при больших межосевых расстояниях.
Рис. 12.8. Механизм с гибкой связью
12.5. Передаточное отношение
В механизмах, предназначенных для передачи вращательного движения (фрикционных, зубчатых и др.), основным кинематическим параметром является передаточное отношение, представляющее собой отношение угловых скоростей звеньев:
Очевидно, что
При параллельных осях вращения звеньев передаточное отношение считается положительным, если направления угловых скоростей звеньев одинаковые, и отрицательным, если эти направления противоположные (см. рис. 12.7). Передаточное отношение может быть выражено через параметры механизма:
где r 1и r 2 – радиусы фрикционных катков; z 1 и z 2 – числа зубьев колес в случае зубчатой передачи.
Глава 13. Основы расчета и проектирования механизмов
13.1. Общие сведения о передачах. Основные виды зубчатых передач
Передачами в машинах называются устройства, предназначенные для передачи энергии механического движения на расстояние и преобразования его параметров. Необходимость применения обусловлена несовпадением требуемых скоростей движения исполнительных органов с оптимальными скоростями двигателей; преобразованием видов движения (вращательного в поступательное), регулированием скорости, распределением потоков мощности между различными исполнительными органами машины, реверсированием движения. По принципу работы механические передачи делятся на передачи с непосредственным соприкосновением звеньев (фрикционные, зубчатые, червячные, волновые, винт-гайка, шарнирно-рычажные) и передачи с гибкой связью(ременные, канатные, цепные). Передачи выполняются с постоянным или переменным (регулируемым) передаточным отношением. В последнем случае регулирование может быть ступенчатое или бесступенчатое. Наряду с механическими широко применяются гидравлические, пневматические и электрические передачи. Зубчатая передача – это трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими между собой высшую пару. Достоинства: высокая надежность работы в широком диапазоне скоростей и нагрузок, малые габариты, большая долговечность, высокий КПД, сравнительно малые нагрузки на валы и подшипники, постоянство передаточного отношения, простота обслуживания. Недостатки: высокие требования к точности изготовления и монтажа, повышенный шум при больших скоростях. В зависимости от расположения осей вращения колес различают следующие виды зубчатых передач: с параллельными осями (цилиндрические), с пересекающимися осями (конические), со скрещивающимися осями. Цилиндрические передачи: с внешним (рис. 13.1, а) и внутренним зацеплением (рис. 13.1, б); частным случаем является реечная передача (рис. 13.1, в), осуществляющая преобразование вращательного движения в поступательное.
а б в
Рис. 13.1. Цилиндрические зубчатые передачи Цилиндрические колеса могут быть с прямыми (рис. 13.2, а), косыми или винтовыми (рис. 13.2, б) и шевронными зубьями (рис. 13.2, в).
а б в
Рис. 13.2. Цилиндрические колеса
Конические передачи чаще всего выполняются ортогональными, у которых межосевой угол ∑ = 90° (рис. 13.3). Конические колеса могут быть с прямыми, тангенциальными и криволинейными (чаще всего круговыми) зубьями (рис. 13.4).
Червячная передача (рис. 13.5) состоит из червяка 1, представляющего собой однозаходный или многозаходный винт, и червячного колеса 2. Зубчатое колесо передачи с меньшим числом зубьев называется шестерней (z 1), а с большим числом зубьев – колесом (z 2).
Рис. 13.5. Червячная передача
По соотношению угловых скоростей ведущего и ведомого звеньев зубчатые передачи делятся на понижающие (редукторы) и повышающие (мультипликаторы). У понижающих передач ведомое звено вращается с меньшей скоростью, чем ведущее (
13.2. Общие сведения о методах изготовления зубчатых колес
Существуют два принципиально различных метода изготовления зубчатых колес – метод копирования и метод обкатки (огибания). При методе копирования профиль инструмента точно совпадает с профилем впадины изготовляемого колеса. В качестве инструмента используются модульная дисковая (рис.13.6) или пальцевая фреза, фасонный резец и др. После обработки каждой впадины заготовка поворачивается на один угловой шаг:
Процесс повторяется до тех пор, пока не будут нарезаны все зубья (τ –центральный угол). Так как форма эвольвенты зависит от радиуса основной окружности, то колёса одного модуля, но с разным числом зубьев должны нарезаться фрезами с различной кривизной эвольвенты. Но бесконечное количество фрез иметь невозможно, поэтому промышленностьюизготавливаются комплекты, состоящие из восьми фрез. Это приводит к неточности изготовления колес. Вторым существенным недостатком метода копирования является низкая производительность труда.
Рис. 13.6. Нарезание зубьев методом копирования
При методе обкатки инструмент и заготовка имеют такое же относительное движение, как два зубчатых колеса в зацеплении. Поэтому инструмент представляет собой колесо с зубьями эвольвентного профиля, заточенными для осуществления резания. Такое инструментальное колесо называется долбяком (рис. 13.7).
Рис. 13.7. Нарезание зубьев методом обкатки Кроме долбяка используются зуборезная рейка с прямолинейными профилями зубьев или червячная фреза, которая в нормальном сечении витков имеет профиль рейки. Преимущества метода обкатки: высокая производительность, большая точность, возможность нарезания колес одного модуля с различными числами зубьев одним и тем же инструментом.
13.3. Кинематика зубчатых механизмов с неподвижными осями вращения
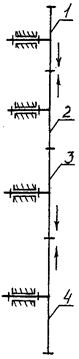
Для получения больших передаточных отношений применяются многоступенчатые передачи, составленные из нескольких простых зубчатых передач. Рассмотрим трехступенчатую передачу (рис. 13.8).
Рис. 13.8. Трехступенчатая передача
Передаточное отношение всего механизма
апередаточное отношение отдельных ступеней –
Перемножим эти отношения:
Сравнивая выражения (13.1) и (13.2), получим
т. е. передаточное отношение многоступенчатой передачи равно произведению передаточных отношений отдельных ступеней. Колеса 1 и 4 вращаются в одну сторону. Таким образом,
Если все ступени являются цилиндрическими передачами, то в общем случае
где k – число внешних зацеплений. Частным случаем многоступенчатой передачи является ступенчатый ряд с промежуточными (паразитными) колесами (рис. 13.9). Передаточное отношение для такой передачи
Промежуточные колеса не влияют на величину общего передаточного отношения, но могут изменять его знак. Такие передачи применяются для изменения направления вращения ведомого звена, а также в случае передачи вращения между удаленными валами. В общем случае
Рис. 13.9. Передача с промежуточными колесами
13.4. Кинематика зубчатых механизмов с подвижными осями вращения
К механизмам с подвижными осями относятся механизмы, в составе которых имеется хотя бы одно колесо с перемещающейся в пространстве осью вращения (сателлит). Различают три вида таких механизмов: 1) дифференциальные; 2) планетарные; 3) замкнутые дифференциальные. Рассмотрим один из простейших дифференциальных механизмов (рис. 13.10). Звенья 1 и 3 – центральные колеса, 2 – сателлит, Н – водило. Водило Н и соосные с ним центральные колеса 1 и 3 называются основными звеньями.
Рис. 13.10. Дифференциальная передача
Получим формулу, связывающую угловые скорости звеньев в дифференциальном механизме. Используем метод обращения движения. Сообщаем всем звеньям механизма дополнительную угловую скорость, равную угловой скорости водила Н, но противоположно направленную, т. е. (
Таким образом, так как
где
Полученное выражение (13.3) называется формулой Виллиса. В общем случае формула Виллиса имеет вид
Если в дифференциальном механизме одно из центральных колес сделать неподвижным, то получится планетарный механизм (рис. 13.11).
Рис. 13.11. Планетарная передача
Так как
Выражение (13.4) называется формулой Виллиса для планетарных механизмов. В общем случае она имеет вид
где индекс b соответствует неподвижному центральному колесу. Планетарные механизмы часто называются планетарными передачами. Они позволяют получать большие передаточные отношения при малых габаритах.
Глава 14. Основы кинематического анализа механизмов
14.1. Задачи и методы кинематического анализа механизмов. Масштабные коэффициенты
Кинематический анализ механизма состоит в определении движения его звеньев по заданному движению начальных звеньев. При этом считается известной кинематическая схема механизма, т. е. его структурная схема с указанием размеров звеньев, необходимых для кинематического анализа. Основные задачи кинематического анализа. 1. Определение положений звеньев и траекторий отдельных точек звеньев. 2. Определение линейных скоростей и ускорений точек, угловых скоростей и ускорений звеньев. 3. Определение передаточных отношений между звеньями. Эти задачи могут решаться графическими, аналитическими и экспериментальными методами.
|




























 ), a у повышающих – наоборот (
), a у повышающих – наоборот (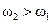 ).
).

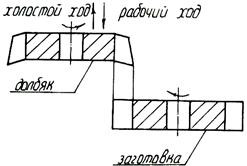

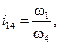 (13.1)
(13.1)
 (13.2)
(13.2)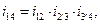


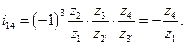



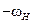 ). При этом относительное движение звеньев не изменится, а угловые скорости в обращенном движении будут следующими:
). При этом относительное движение звеньев не изменится, а угловые скорости в обращенном движении будут следующими:
 то дифференциальный механизм превратился в зубчатый механизм с неподвижными осями. Для такого обращенного механизма
то дифференциальный механизм превратился в зубчатый механизм с неподвижными осями. Для такого обращенного механизма (13.3)
(13.3) – передаточное отношение обращенного механизма, определяемое через число зубьев колес:
– передаточное отношение обращенного механизма, определяемое через число зубьев колес:
 ab
ab
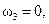 то из формулы
то из формулы  получим:
получим:
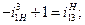
 (13.4)
(13.4)



