Расчеты на жесткость при изгибеВ ряде случаев работающие на изгиб элементы машиностроительных и строительных конструкций должны быть рассчитаны не только на прочность, но и на жесткость. К деталям, рассчитываемым на жесткость, относятся, в частности, валы зубчатых и червячных передач и многие части металлорежущих станков. Расчет на жесткость элемента конструкции, имеющего форму бруса, заключается в определении наибольших перемещений его поперечных сечений и сопоставлении их с допускаемыми, зависящими от назначения и условий эксплуатации данного элемента. Рассмотрим простую консоль, нагруженную на свободном конце силой F, линия действия которой совпадает с одной из главных осей поперечного сечения балки (рис. 19.10).
Рис. 19.10. Линейное и угловое перемещения сечения при изгибе При деформации балки центры тяжести ее поперечных сечений получают линейные перемещения, а сами сечения поворачиваются вокруг своих нейтральных осей. Допущение о малости перемещений позволяет считать, что направления линейных перемещений перпендикулярны продольной оси недеформированного бруса. Эти перемещения принято называть прогибами. Прогиб произвольного сечения обозначим ν, а наибольший прогиб – стрелу прогиба – f. Геометрическое место центров тяжести поперечных сечений деформированного бруса, т. е. ось изогнутого бруса, условно называют изогнутой осью, или, чаще, упругой линией. Угол поворота θ поперечного сечения равен углу между касательной к упругой линии в данной точке и осью недеформированного бруса. Вывод: ордината упругой линии и угол наклона касательной, проведенной к ней в данной точке, полностью определяют линейное и угловое перемещения соответствующего поперечного сечения балки. В большинстве случаев условие жесткости выражается неравенством
т. е. максимальный прогиб (стрела прогиба f) не должен превышать допускаемого Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений:
При этом допускаемый угол поворота составляет в среднем 0, 001 радиан. 19.6. Кручение вала (стержня) круглого поперечного сечения
Кручение – это такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент, обозначаемый Mz или Tk. На рис. 19.11 изображен брус, работающий на кручение под действием приложенных к нему скручивающих моментов (M 1, M 2, M 3, М 4). Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна нулю, т. е. брус находится в равновесии. Применяя метод сечений и рассматривая равновесие оставленной части (рис. 19.12), приходим к выводу, что внутренние силы, возникающие в поперечном сечении бруса, должны дать момент (крутящий момент), уравновешивающий внешние моменты, приложенные к оставленной части.
Итак, крутящий момент, возникающий в произвольном поперечном сечении бруса, численно равен алгебраической сумме скручивающих моментов, приложенных к оставленной части. При кручении бруса в его поперечных сечениях возникают только касательные напряжения. Для расчета на прочность, так жекак и при растяжении (сжатии) бруса, надо найти его опасное сечение. В случае, если размеры поперечного сечения по длине бруса постоянны, опасными будут сечения, в которых крутящий момент максимален. График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов (см. рис. 19.12). Правило знаков: будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке (рис. 19.13). Соответствующий внешний момент направлен против часовой стрелки.
Рис. 19.13. Правило знаков для Mz
19.7. Расчеты на прочность и жесткость при кручении
Прочность бруса, работающего на кручение, считают обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном сечении, не превышают допускаемых:
Конечно, незначительное (до 5–6 %) превышение расчетного напряжения над допускаемым не опасно. Эпюры касательных напряжений для круглого сплошного и кольцевого поперечных сечений показаны на рис. 19.14.
Рис. 19.14. Эпюры касательных напряжений поперечных сечений вала
В точках, равноудаленных от центра сечения, напряжения одинаковы. Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения:
где Введя обозначение
Величину
Эта формула служит для проверочного расчета на прочность. При проектном расчете и при определении допускаемой нагрузки (момента) из формулы (19.4) соответственно находят Для кольца
и для круга
Для конструкционной углеродистой стали обычно Во многих случаях вал должен быть рассчитан не только на прочность, но и на жесткость при кручении. Рассмотрим брус, жестко защемленный одним концом и нагруженный на свободном конце скручивающим моментом М (рис. 19.15). При деформации бруса его поперечные сечения повернутся на некоторые углы по отношению к своему первоначальному положению или, что то же самое, по отношению к неподвижному сечению (заделке). Угол поворота будет тем больше, чем дальше отстоит данное сечение от заделки. Так, для произвольного сечения I, отстоящего от заделки на расстоянии z, он равен Вообще, угол поворота вала при включении произвольного сечения равен углу закручивания части бруса, заключенной между этим сечением и заделкой. Таким образом, угол поворота φ торцового сечения представляет собой полный угол закручивания рассматриваемого бруса. За меру жесткости при кручении принимают относительный угол закручивания (угол закручивания на единицу длины) вала, обозначаемый φ 0 (встречается обозначение θ):
Рис. 19.15. Деформации вала при кручении
Угол закручивания бруса постоянного диаметра при одинаковом во всех поперечных сечениях крутящем моменте равен
где l – длина рассматриваемого участка, мм. В отличие от допускаемого напряжения, зависящего в первую очередь от материала вала, допускаемый угол закручивания зависит от назначения вала. Значения допускаемых углов закручивания, встречающихся в различных отраслях машиностроения, весьма разнообразны; наиболее распространены значения [θ ] = (4, 38–17, 5) · 103 рад/м = 0, 25–1, 0 град/м. Условие жесткости при кручении имеет вид
где При проектном расчете отсюда определяют требуемое значение Ip:
а затем вычисляют диаметр вала. Из двух значений диаметра вала, определенных из расчетов на прочность и жесткость, в качестве окончательного (исполнительного размера) должен быть, конечно, принят больший. Для круга
19.8. Условие прочности вала при совместном действии крутящего и изгибающего моментов
При ориентировочном расчете валов влияние изгиба не учитывалось, но допускаемые напряжения на кручение принимались весьма невысокими, что должно было в известной мере компенсировать ошибку, являющуюся следствием пренебрежения изгибом. Применение гипотез прочности позволяет рассчитывать валы, учитывая совместное действие изгиба и кручения. При расчете валов, а также других элементов конструкций, испытывающих одновременное действие изгиба и кручения, влиянием поперечных сил, как правило, пренебрегают, так как соответствующие им касательные напряжения в опасных точках бруса, невелики по сравнению с касательными напряжениями от кручения и нормальными напряжениями от изгиба. На рис. 19.16, а показан вал, на который насажены зубчатое колесо диаметром
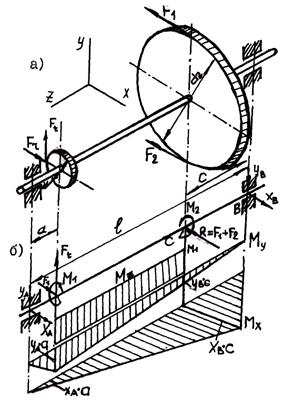
Рис. 19.16. Изгиб с кручением вала
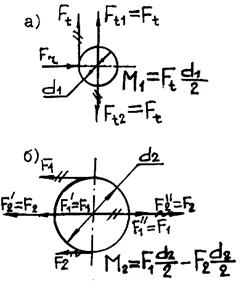
Рис. 19.17. Перенос сил к оси вала
При равномерном вращении вала (только такой случай и рассматривается) На основе расчетной схемы определяют опорные реакции и строят эпюры
Для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий Валы, как правило, изготовляют из среднеуглеродистой конструкционной или реже – легированной стали. Их расчет выполняют на основе третьей или пятой гипотез прочности. Составим расчетную зависимость по третьей гипотезе прочности. По формуле
подставляя в нее значения
Учитывая, что для круглого (сплошного или кольцевого) сечения
Внешне эта формула аналогична расчетной зависимости для определения максимальных нормальных напряжений при изгибе, поэтому величину, стоящую в числителе, называют эквивалентным (или приведенным) моментом, при этом условие прочности имеет вид
Расчет бруса круглого поперечного сечения на изгиб с кручением ведется аналогично расчету на изгиб, но вместо изгибающего момента в расчетную формулу входит так называемый эквивалентный момент, который зависит от изгибающих и крутящего моментов, а также от принятой гипотезы прочности. По гипотезе наибольших касательных напряжений,
При проектном расчете определяют требуемое значение момента сопротивления поперечного сечения:
Учитывая, что для сплошного круглого сечения
Понятие «эквивалентный момент» не имеет смысла при изгибе с кручением бруса некруглого поперечного сечения. Неприменимо оно и в случае, если помимо изгиба и кручения брус круглого сечения испытывает растяжение или сжатие. Для бруса с постоянным диаметром опасная точка находится в сечении, для которого эквивалентный момент имеет наибольшее значение. Это сечение также называют опасным. Для отыскания опасного сечения иногда помимо эпюр
Глава 20. Устойчивость сжатых элементов Конструкций
20.1. Понятие о критической силе для сжатого стержня. Формула Эйлера
Из физики известно, что равновесие тела устойчиво, если при малом отклонении от равновесного положения возникает сила или пара сил, возвращающая его в положение равновесия. Кроме устойчивого известны также неустойчивое и безразличное равновесия, но для механических конструкций допустимы лишь случаи устойчивого равновесия. Если по каким-либо причинам упругое тело или конструкция при отклонении от равновесного положения не возвращается к исходному, то говорят, что произошла потеря устойчивости. Явление потери устойчивости упругого тела рассмотрим на примере сжатого стержня. Представим, что на прямолинейный стальной стержень, зажатый одним концом в вертикальном положении (рис. 20.1, а) сверху надет шар. При небольшом значении силы тяжести G 1, сжимающей стержень, он сохраняет прямолинейную форму и находится в устойчивом равновесии. Действительно, если отклонить шар вместе с верхней частью стержня в сторону, то под действием упругих сил стержень, поколебавшись около положения равновесия, снова примет прямолинейную форму. Постепенно увеличивая сжимающую нагрузку путем установки более тяжелых шаров (рис. 20.1, б), увидим, что стержень хотя и сохраняет прямолинейную форму, но при отклонении от положения равновесия возвращается в исходное положение гораздо медленнее. Наконец, при некоторой нагрузке G 3 (рис. 20.1, в) стержень изогнется, и прямолинейная форма устойчивого равновесия переходит в новую, криволинейную форму устойчивого равновесия.
Рис. 20.1. Потеря устойчивости
Если теперь стержень принудительно выпрямить или, наоборот, изогнуть еще больше, он после нескольких колебаний займет исходное равновесное положение в изогнутом состоянии. Максимальная сжимающая нагрузка Смысл расчета на устойчивость сжатого стержня заключается в том, чтобы он при некотором значении F осевой нагрузки сохранял устойчивость прямолинейной формы и обладал при этом некоторым запасом устойчивости (рис. 20.2):
Рис. 20.2. К определению запаса устойчивости
Условие устойчивости сжатого стержня
где Допускаемая сжимающая сила
Задачу определения критической силы впервые чисто математически решил Л. Эйлер в 1744 г. Формула Эйлера имеет вид
где
Экспериментальные исследования, связанные с проверкой формулы Эйлера, показывают, что при прочих равных условиях (одинаковые материал, форма и размеры поперечного сечения, а также длина стержня) значение критической силы зависит от способа закрепления его концов.
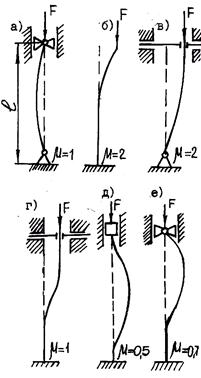
Рис. 20.3. Значения коэффициента приведения длины стержня при различных способах закрепления его концов На рис. 20.3 изображены несколько случаев закрепления стержня и указаны соответствующие значения коэффициента приведения μ: – оба конца шарнирно закреплены (рис. 20.3, а); – один конец жестко закреплен, другой – свободен (рис. 20.3, б); – один конец закреплен шарнирно, второй имеет «плавающую» заделку (рис. 20.3, в); – один конец заделан жестко, второй имеет «плавающую» заделку (рис. 20.3, г); – оба конца заделаны жестко (рис. 20.3, д); – один конец заделан жестко, другой закреплен шарнирно (рис. 20.3, е).
20.2. Критическое напряжение. Пределы применимости формулы Эйлера
При осевом нагружении стержня в его поперечных сечениях возникают нормальные напряжения сжатия, которые возрастают по мере увеличения нагрузки. Нормальные напряжения, соответствующие критической силе, называются критическими:
После подстановки значения критической силы из формулы (20.1) получим
Линейную величину Таким образом,
Безразмерная величина Определяя значение критической силы, Эйлер исходил из рассмотрения упругой линии изогнутого стержня, поэтому формула
справедлива только в пределах применимости закона Гука, иначе говоря, до тех пор, пока критическое напряжение не превышает предела пропорциональности материала стержня, т. е. при условии
Отсюда
Стоящая в правой части неравенства постоянная для данного материала безразмерная величина называется предельной гибкостью:
Применимость формулы Эйлера определяется условием Формула Эйлера применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен. Как правило, многие конструкции имеют стержни с гибкостью меньше предельной. РАЗДЕЛ 4 РАСЧЕТ И КОНСТРУИРОВАНИЕ ДЕТАЛЕЙ МАШИН ОБЩЕГО НАЗНАЧЕНИЯ И ДЕТАЛЕЙ ОТРАСЛИ
Глава 21. ЗУБЧАТЫЕ ПЕРЕДАЧИ
21.1. Геометрический расчет эвольвентных прямозубых передач
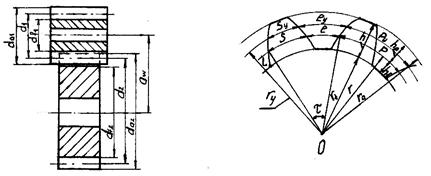
Рассмотрим сечение цилиндрического зубчатого колеса (рис. 21.1) с внешними зубьями плоскостью, перпендикулярной к оси колеса (главное, или торцовое сечение). Выделяют окружность вершин зубьев (
Рис. 21.1. Сечение цилиндрического зубчатого колеса
Эвольвентный профиль и окружность впадин соединяются переходной кривой. Общая точка L эвольвенты и переходной кривой называется граничной точкой профиля. Расстояние между одноименными профилями двух соседних зубьев, измеренное по дуге окружности, называется окружным шагом зубьев. Для окружности произвольного радиуса
где py – окружной шаг; Sy – окружная толщина зуба; ey – окружная ширина впадины. Длину окружности можно выразить через шаг py и число зубьев z:
откуда
где Модуль и шаг зависят от окружности, к которой они относятся. На колесе выделяется расчетная окружность, на которой шаг и модуль зубьев равны шагу и модулю зуборезного инструмента. Эта окружность называется делительной (r, d), а модуль зубьев на делительной окружности называется расчетным модулем зубчатого колеса:
где p – шаг по делительной окружности (делительный шаг). Значения m регламентированы СТ СЭВ 310–76, ГОСТ 9563–80: 1-й ряд – 0, 8; 1; 1, 25; 1, 5; 2; 2, 5; 3; 4; 5 и т. д.; 2-й ряд – 0, 9; 1, 125; 1, 375; 1, 75; 2, 25; 2, 75 и т. д. Диаметр делительной окружности
Центральный угол
В основе зуборезного инструмента, используемого для нарезания эвольвентных цилиндрических колес по методу обкатки, лежит исходный производящий контур, под которым понимается контур зубьев зуборезной рейки в сечении плоскостью, перпендикулярной к направлению ее зубьев. Параметры этого контура стандартизованы (СТ СЭВ 308–76 для
Рис. 21.2. Параметры исходного контура зубчатой рейки
Высота зуба исходного производящего контура
где
Угол α = 20° называется углом главного профиля. Прямая, по которой толщина зуба равна ширине впадины, называется делительной. Зубчатые колеса бывают: 1) без смещения исходного контура (некорригированные); 2) со смещением. Если делительная прямая исходного производящего контура касается делительной окружности нарезаемого колеса, то нарезается колесо без смещения, в противном случае нарезается колесо со смещением (рис. 21.3).
Рис. 21.3. Колеса со смещением и без смещения
В зависимости от коэффициентов смещения зацепляющихся колес различают следующие типы передач: 1) передача без смещения (x 1 = x 2 = 0); 2) равносмещенная передача (x 1 = – x 2 ≠ 0, x ∑ = x 1 + x 2 = 0); 3) положительная передача (x ∑ > 0); 4) отрицательная передача (x ∑ < 0). В передачах без смещения и равносмещенных[1]
Межосевые расстояния для стандартных редукторов нормированы:
При нарезании зубьев без смещения можно изготовить колесо лишь с z 1min ≥ 17 (если x ∑ > 0, то z 1min = 12). При окружных скоростях колес Расчет геометрических параметров цилиндрических зубчатых передач выполняется по ГОСТ 16530–83.
21.2. Особенности геометрии косозубых, шевронных и конических передач
Развернем на плоскость поверхность делительного цилиндра (рис. 12.4). Угол β называется углом наклона линии зуба. Два колеса в зацеплении должны иметь одинаковые углы β, причем при внешнем зацеплении направление винтовых линий у них разное (на одном колесе – правое, а на другом – левое).
Рис. 12.4. Развертка поверхности делительного цилиндра на плоскость У косозубых колес различают окружной шаг pt (в торцовом сечении), нормальный шаг pn (в нормальном сечении) и соответственно окружной (торцовый) модуль Стандартным расчетным модулем является нормальный модуль, т. е. m = mn. Очевидны следующие соотношения:
Зацепление косозубых колес в торцовом сечении аналогично зацеплению прямозубых колес. Поэтому геометрический расчет косозубых колеc производится по формулам для прямозубых колес с подстановкой в них параметров торцового сечения. Например, диаметры делительных окружностей определяются по формулам
В косозубой передаче каждый зуб входит в зацепление не сразу по всей длине, а постепенно. Для передач (
Угол наклона линии зуба назначают β =8–15º, для шевронных β = 30–45°. Угол β < 8° выполнять не следует, так как утрачиваются преимущества косозубых передач перед прямозубыми.
21.3. Особенности геометрии конических колес
Конические зубчатые передачи служат для передачи вращения между валами с пересекающимися осями. Угол между осями (межосевой угол)
Рис. 21.5. Основные геометрические параметры конических колес
Так как зубья на боковых поверхностях конусов отличаются от зубьев цилиндрических колес тем, что их размеры (толщина, высота) по мере приближения к вершине конуса уменьшаются, то соответственно изменяются шаг и модуль зацепления, а также и диаметры вершин, делительный и впадин зубьев. Основные параметры зацепления конической прямозубой передачи
где de – внешний делительный диаметр; z – число зубьев шестерни и колеса;
где
Внешнее конусное расстояние
Модуль Диаметры вершин зубьев и впадин конического зубчатого колеса:
Передаточное число при
Среднее конусное расстояние 21.4. Усилия в зацеплении зубчатых передач
При определении сил в зацеплении используют методы теоретической механики, а силами трения пренебрегают ввиду их малости. Нормальная сила Fn направлена по линии зацепления (как по общей нормали к рабочим поверхностям зубьев). Прямозубая цилиндрическая передача (рис. 21.6).
Рис. 21.6. Силы, действующие в зацеплении прямозубых цилиндрических колес
Силу Fn раскладывают на окружную Ft и радиальную Fr составляющие:
где
|
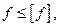
. Значение допускаемого прогиба зависит от назначения и условий работы рассчитываемой конструкции и колеблется в широких пределах. Обычно допускаемую стрелу прогиба указывают в долях пролета (межопорного расстояния l) балки. Например, для ручных грузоподъемных кранов 
, для электрических 
, для валов и шпинделей металлорежущих станков 
– полярный момент инерции.
, получим следующее выражение для максимального касательного напряжения:
, мм3, равную отношению полярного момента инерции сечения к его радиусу, называют полярным моментом сопротивления сечения. Его размерность – L 3. Очевидно, полярный момент сопротивления является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении:
(19.4)
.
= 20–35 МПа.
, для сечения II – 
.Здесь 
– угол поворота сечения II относительно I или угол закручивания элемента бруса длиной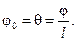 
– условная жесткость сечения круглого бруса при кручении. Модуль сдвига G характеризует жесткость материала, а полярный момент инерции 
и шкив ременной передачи диаметром 
. На зубчатое колесо действуют окружная 
и радиальная 
силы, на шкив – силы 
и 
натяжения ветвей ремня. Для составления расчетной схемы вала (рис. 19.16, б) все силы должны быть приведены к его оси. При переносе силы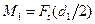 
(рис. 19.17, а); аналогично при приведении сил 
(рис. 19.17, б).
, что следует из основного уравнения динамики для вращательного движения.
, по которым определяют опасное сечение вала.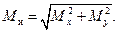
и изгибающий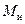 
моменты. В рассматриваемом случае опасным будет сечение C под серединой шкива.
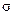и 
, получаем
, имеем
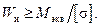
, получаем следующую формулу для определения требуемого диаметра вала: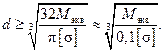
строят эпюру 
. Практически в этом нет необходимости; в случае, если по эпюрам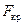 
, при которой прямолинейная форма стержня устойчива, называется критической силой.
– коэффициент запаса устойчивости.
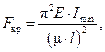(20.1)
– минимальное значение момента инерции площадки поперечного сечения стержня, так как потеря устойчивости происходит в плоскости наименьшей жесткости;
–длина стержня;
– коэффициент приведения длины, т. е. число, показывающее, во сколько раз следует увеличить длину шарнирно закрепленного с обоих концов стержня, чтобы критическая сила для него была равна критической силе стержня в данных условиях закрепления.
(20.2)
называют минимальным радиусом инерции сечения.
и формула (20.2) принимает вид
или 
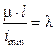называется гибкостью стержня. Она характеризует сопротивляемость стержня потере устойчивости; с увеличением гибкости уменьшается сопротивляемость стержня потере устойчивости. Заметим, что гибкость λ стержня не зависит от материала стержня, а определяется его длиной, формой и размерами сечения.
) и окружность впадин (
), между которыми заключен зуб колеса. Высота зуба 
.
–окружной модуль.
называется угловым шагом зубьев.
), ГОСТ 13755–81 (рис. 21.2).
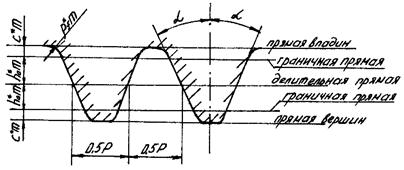
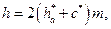
– коэффициент высоты головки зуба;
– коэффициент радиального зазора.
(угол зацепления равен углу главного профиля), 
(делительные окружности одновременно являются и начальными), высота зуба h = 2, 25 m. В передачах без смещения
= 40; 50; 63; 80; 100; 125; 160; 180; 200; 225; 250; 280; 315 и т. д.
, z 1 и z 2 принимают кратными друг другу; при 
, для z 1 и z 2 принимают взаимно простые числа зубьев.
, нормальный модуль 
.
) x 1 = x 2 = 0
теоретически может быть в диапазоне 10°< 
< 170º. Наибольшее распространение получили передачи с углом 
и 
– углы делительного конуса шестерни и колеса. Конические прямозубые колеса нарезаются на зуборезных станках инструментами, в основу которых положен зуб исходной рейки (ГОСТ 13754–81, 
= 1; 
; 
) (рис. 21.5).
– средний делительный диаметр;
– средний окружной модуль;
–внешний окружной модуль, значения которого согласуют с СТ СЭВ 310–76, ГОСТ 13755–81.
–коэффициент ширины зубчатого венца;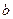
–ширина зубчатого венца;
–внешнее конусное расстояние.
и ножки 
.
.
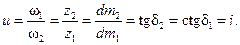
– сила, изгибающая зуб;
– сила, сжим
