Допустимая растягивающая нагрузка
Соединение комбинированным (лобовым и фланговым) швом при действии момента в плоскости стыка при упрощенном расчете рассчитывают, полагая, что швы работают независимо. Тавровые соединения, выполненные угловыми швами, рассчитывают по формуле
с учетом числа швов. Момент сопротивления продольного сечения шва
где h – высота листа ( Если такие соединения сварены, как и соединения встык, то расчет выполняют по формулам (26.1) и (26.3). Угловые соединения не используются как силовые; их применяют, как правило, для образования профилей из отдельных элементов.
26.3. Соединения пайкой и склеиванием
При соединении пайкой в отличие от сварки место спайки нагревается лишь до температуры плавления припоя, которая намного ниже температуры плавления материала соединяемых деталей. Соединение деталей получается благодаря заполнению зазора между ними расплавленным припоем. Швы неразъемных соединений, получаемые пайкой и склеиванием, условно изображают по СТ СЭВ 138–76. Припой или клей в разрезах (рис. 26.11, а, б, г, д, е) и на видах (рис. 26.11, в)изображают линией, которая в два раза толще основной сплошной. Для обозначения пайки (рис. 26.11, а, б, в) или склеивания (рис. 26.11, г, д, е) применяют условные знаки, которые наносят на линии-выноске от сплошной основной линии. Швы, выполненные пайкой или склеиванием по периметру, обозначаются линией-выноской, заканчивающейся окружностью диаметром 3–4 мм (рис. 26.11, б, д). На изображении паяного соединения при необходимости указывают размеры шва и обозначения шероховатости поверхности. В соединениях пайкой и склеиванием место соединения элементов в разрезах и на видах показывают утолщенной (в два раза) контурной линией. Если же соединяемые элементы показаны в сечении зачерненными, то место соединения изображается просветом. Обозначение соединений пайкой и склеиванием производится с помощью символов и знаков, проставляемых на линии-выноске, которая заканчивается стрелкой, указывающей непосредственно шов, или точкой при указании невидимых частей соединения. Для пайки применяется символ На полке линии-выноски ставится номер пункта технических требований, где указана марка припоя или клея.
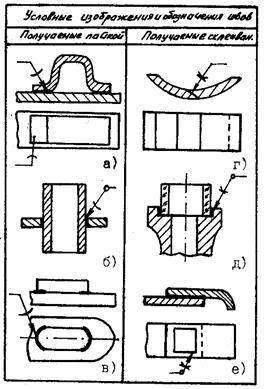
Рис. 26.11. Паяные и клеевые соединения
26.4. Соединения типа «вал–ступица». Общая характеристика и особенности расчета
Для передачи вращения от вала к ступице зубчатого колеса, шкива, звездочки и других соосных деталей широко используют различные соединения зацеплением. В соединениях зацеплением (шпоночных, шлицевых и др.) передача нагрузки осуществляется за счет силового замыкания деталей через шпонки, зубья и другие подобные детали. Благодаря этому соединения являются разъемными, осуществляют фиксацию деталей в окружном направлении и допускают осевое взаимное смещение деталей в процессе работы. Однако трудоемкость изготовления таких соединений довольно высокая. 26.4.1. Шпоночные соединения
Соединение двух соосных цилиндрических деталей (вала и ступицы) для передачи вращения между ними осуществляется с помощью шпонки 1 – специальной детали, закладываемой в пазы соединяемых вала 2 и ступицы 3 (рис. 26.12).
Рис. 26.12. Соединение призматической шпонкой
В машиностроении применяют ненапряженные (без нагрузки) соединения (с помощью призматических и сегментных шпонок) и напряженные (с помощью клиновых шпонок). Шпонки этих типов стандартизованы, их размеры выбирают по ГОСТ 23360–78, ГОСТ 24071–80 и ГОСТ 24068–80. Основные достоинства соединений: простота конструкции и воз–можность жесткой фиксации насаживаемой детали в окружном направлении. Однако соединения трудоемки в изготовлении, требуют ручной пригонки или подбора. Это ограничивает использование соединений в машинах крупносерийного и массового производства. Не рекомендуется применение соединений для быстро вращающихся валов ответственного назначения из-за сложности обеспечения концентричной посадки сопрягаемых деталей. Основным для соединений призматическими шпонками является условный расчет на смятие (упругопластическое сжатие в зоне контакта). Если принять для упрощения, что напряжения в зоне контакта распределены равномерно и плечо равнодействующей этих напряжений равно 0, 5 d (где d – диаметр вала), то средние контактные напряжения (напряжения смятия, вызывающие смятие рабочих граней)
где T – вращающий момент; l p – рабочая длина шпонки (см. рис. 26.12); t 2 = 0, 4 h – глубина врезания шпонки в ступицу;
На практике сечение шпонки подбирают по ГОСТ 23360–78 в зависимости от диаметра вала, а длину l шпонки назначают на 5–10 мм меньше длины ступицы. Затем по формуле (26.4) оценивают прочность соединения на смятие или вычисляют предельный момент, соответствующий напряжению
26.4.2. Шлицевые соединения
Общие сведения. Шлицевое соединение условно можно рассматривать как многошпоночное, у которого шпонки выполнены как одно целое с валом. По сравнению со шпоночными соединениями они имеют меньшие радиальные габариты, высокую несущую способность, взаимозаменяемы и обеспечивают хорошее центрирование деталей. Эти преимущества позволяют использовать соединения в условиях массового производства конструкций и при большей частоте вращения валов (рис. 26.14). По форме поперечного сечения различают три типа соединений: прямобочные ГОСТ 1139–80; эвольвентные ГОСТ 6033–80; треугольные (изготовляются по отраслевым стандартам). Проектирование и расчет соединений. Основные размеры (наружный диаметр D и длину l) шлицевого соединения задают при конструировании вала. Длину соединения принимают не более 1, 5 D; при большей длине существенно возрастают неравномерность распределения нагрузки вдоль зубьев и трудоемкость изготовления.
Рис. 26.13. Расчетная схема зуба шлицевого соединения
Учитывая, что соединения в машинах выходят из строя преимущественно из-за повреждения рабочих поверхностей зубьев (смятие, износ) и усталостного разрушения шлицевых валов, после проектирования выполняют проверочный расчет зубьев. Условие прочности по допускаемым напряжениям смятия имеет вид
где dm – средний диаметр соединения; z – число зубьев; h и l– соответственно высота и длина поверхности контакта зубьев; ψ – коэффициент, учитывающий неравномерное распределение нагрузки между зубьями и вдоль зубьев (ψ = 0, 5–0, 7);
26.4.3. Профильные соединения
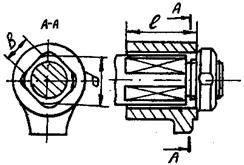
Общие сведения. Профильными называют соединения, в которых ступица (втулка) насаживается на фасонную поверхность вала и таким образом обеспечивается жесткое фиксирование деталей в окружном направлении и передача вращения (рис. 26.14).
Рис. 26.14. Профильное соединение
Профильные соединения рассчитывают на смятие. Условие прочности по допускаемым напряжениям для соединения
где l – длина соединения, обычно l = (1–2) d; b – ширина прямолинейной части грани;
26.4.4. Штифтовые соединения
Штифтовые соединения применяют при небольших нагрузках, преимущественно в приборостроении. Основные типы штифтов стандартизованы. Их изготовляют из углеродистых сталей 30, 45, 50 и др. Штифтовое соединение работает на срез и смятие. Для расчета соединения используют те же зависимости. Условие прочности при срезе радиального штифта (рис. 26.15)
а условие прочности на смятие
где Ft – срезающая сила (осевая или окружная); i – число поверхностей среза;
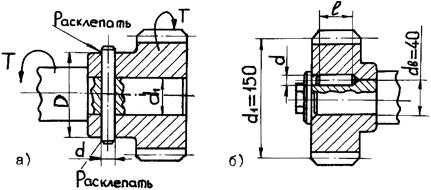
Рис. 26.15. Схемы к расчету соединений радиальным (а) и осевым (б) штифтами: d – диаметр штифта; d 1 – диаметр вала
Срезающая сила при передаче вращающего момента Осевые штифты (круглые шпонки) применяют в машиностроении для передачи вращающего момента в неразъемных соединениях. Штифты диаметром d = (0, 1–0, 15) d ви длиной l = (3–4) d в (d в – диаметр вала) устанавливают по посадке с натягом Н 7/ r 6 в отверстия, совместно просверленные и развернутые при сборке в валу и ступице по стыку посадочных поверхностей (рис. 26.15, б). Материалы детали и вала должны иметь примерно одинаковую твердость для исключения увода сверла в сторону менее твердого материала. Число штифтов для передачи заданного вращающего момента
Многоштифтовые соединения этого типа по прочности близки к шлицевым.
26.5. Резьбовые соединения
Резьбовыми называют соединения деталей с помощью резьбы. Они являются наиболее распространенным видом разъемных соединений.
26.5.1. Крепежные детали и стопорящие устройства
Наибольшее распространение среди резьбовых деталей получили крепежные болты, винты, шпильки, гайки. Под болтом или винтом понимают стержень с головкой и одним резьбовым концом. Шпилька имеет два резьбовых конца. Гайка – это деталь с резьбовым отверстием. С помощью этих деталей образуют разъемные соединения болтом, винтом и шпилькой в разнообразных конструкциях. Тип соединения определяется прочностью материалов соединяемых деталей, частотой сборки и разборки соединений в эксплуатации, а также особенностями конструкции и технологии изготовления соединяемых деталей. Для предохранения повреждений поверхностей соединяемых деталей при завинчивании и увеличения опорной поверхности гайки используют шайбы. При статических нагрузках самоотвинчивания резьбовых деталей не наблюдается, так как все крепежные резьбы выполняются самотормозящимися (явление самоотвинчивания не должно наблюдаться). При динамических и вибрационных нагрузках может произойти самоотвинчивание гаек и винтов. Для предотвращения самоотвинчивания резьбовых деталей применяют различные средства стопорения. Основные из них – контргайки, пружинные шайбы, стопорные шайбы, шплинты. Если не требуется разборка соединения, гайки устанавливают внаклеп, производят кернение, расклепывание и приварку. Штифты, винты, упругие контргайки, проволока также могут выполнять функции стопорения. Болты, винты, шпильки и гайки изготавливают из мало- и среднеуглеродистых сталей Ст 3 кп, Ст 5, 10, 10 кп, 15, 20, 30, 45 и др. В ответственных случаях (ударные нагрузки, высокие температуры) применяют легированные стали 40Х, 38ХА, 30ХГСА, 35ХГСА, 40ХН2МА и др., а также титановые сплавы (резьбовые детали из титановых сплавов по сравнению со стальными имеют повышенную прочность и примерно в два раза легче). Пружинные шайбы изготавливают из рессорно-пружинных сталей 65, 70, 75, 65Г. Гайки изготавливают из стали Ст 3. Механические характеристики материалов крепежных деталей нормированы ГОСТ 1759–82. Для стальных болтов, винтов и шпилек предусмотрено 12, а для гаек – семь классов прочности и соответствующие им марки сталей.
26.5.2. Резьба и ее параметры
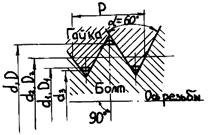
Резьба является основным элементом резьбового соединения. Она образует выступы по винтовой линии на поверхности винта и гайки (наружная и внутренняя), может изготавливаться на цилиндрической (цилиндрическая резьба) и конической (коническая резьба) поверхностях заготовки, бывает правая, если винтовая линия направлена вверх слева направо, и левая – при направлении ее вверх права налево. Наиболее применяемые правые резьбы. Если на поверхность детали наносится один винтовой выступ, резьбу называют однозаходной. Применяют также многозаходные резьбы. Основные параметры цилиндрической резьбы (рис. 26.16): d, D – наружные диаметры соответственно болта и гайки; d 1, D 1; d 2, D 2 – внутренние и средние диаметры резьбы; d 3 – внутренний диаметр болта по дну впадины; Р – шаг (расстояние между одноименными сторонами двух смежных профилей); ψ – угол подъема резьбы, т. е. угол развертки винтовой линии по среднему диаметру резьбы: ph – ход резьбы (осевое перемещение гайки за один оборот): для однозаходной резьбы ph = p, для многозаходной ph = n · p, где n – число заходов резьбы (рис. 26.17).
По форме профиля крепежные резьбы бывают треугольные и круглые; резьбы винтовых механизмов (ходовые резьбы) – трапецеидальные, упорные, прямоугольные. Метрическая резьба (ГОСТ 24705–81) – основной вид резьбы крепежных деталей (см. рис. 26.16). Она бывает с крупным и мелким шагом, но чаще выполняют наиболее износостойкую и технологичную резьбу с крупным шагом. Дюймовая резьба подобна метрической (α = 55°, у метрической α = 60°). Трубные резьбы (цилиндрическая и коническая) служат для соединения труб и арматуры. Трапецеидальная резьба технологична, отличается высокой прочностью витков и является основной для винтовых механизмов. Упорная резьба имеет несимметричный профиль витков и выполняется на винтах, воспринимающих значительную одностороннюю нагрузку. Прямоугольная резьба сложна в изготовлении и применяется редко. Геометрические параметры резьб (кроме прямоугольной) и их допуски стандартизованы. Резьбу получают методом резания, накатыванием, литьем и прессованием.
26.5.3. Силовые зависимости в резьбовом соединении
Надежность резьбового соединения оценивается легкостью сборки (легкостью затяжки гайки или болта) и сохранностью затяжки (самоторможением). При завинчивании гайки надо преодолеть момент сопротивления затяжки Т 3 = T р + T т,
где T р – момент сил трения в резьбе; Т т – момент сил трения на опорном торце гайки. Для определения Т р и Т т необходимо установить зависимость между силами, возникающими в винтовой паре при завинчивании. Развернем среднюю винтовую линию резьбы на плоскость, а гайку представим в виде ползуна (рис. 26.18, а).

Рис. 26.18. К анализу сил в винтовой паре
При подъеме ползуна по наклонной плоскости (это соответствует завинчиванию гайки) сила F взаимодействия наклонной плоскости с движущимся ползуном представляет собой равнодействующую нормальной силы и силы трения. Из схемы сил, действующих на ползун (рис. 26.18, б),
где
f – коэффициент трения. При перемещении ползуна вниз (рис. 26.18, в)
где Полагая, что сила Ft сосредоточена и приложена к среднему радиусу резьбы 0, 5 d 2 (см. рис. 26.19, а):
Силу трения на торце гайки f 1· F, зависящую от коэффициента трения f 1 на торце гайки, считают сосредоточенной и приложенной к среднему радиусу опорной поверхности (рис. 26.19, а):
Момент завинчивания гайки T з, прикладываемый к ключу:
Момент сопротивления затяжки T з преодолевается моментом силы, приложенной к гаечному ключу (рис. 26.19, б). Приравняв оба момента, получим

Рис. 26.19. К определению момента завинчивания
Величины, входящие в формулу (26.7), имеют определенные значения. Например, при стандартном ключе
26.5.4. Самоторможение и коэффициент полезного действия винтовой пары
Если при опускании ползуна по наклонной плоскости (см. рис. 26.18, в)
Для крепежных резьб угол подъема резьбы Коэффициент полезного действия винтовой пары определяют как отношение
С увеличением 26.5.5. Расчет резьбовых соединений на прочность
Виды разрушения резьбовых крепежных деталей: разрыв стержня по резьбе или переходному сечению у головки; повреждение или разрушение резьбы (смятие и износ, срез, изгиб); повреждение головки болта (винта). Размеры стандартных болтов, винтов и шпилек отвечают условию равнопрочности всех элементов соединения. Поэтому можно ограничиваться расчетом по одному, основному критерию – прочности нарезной части, а размеры винтов, болтов и гаек принимать по таблицам стандарта в зависимости от рассчитанного диаметра резьбы. Длину болта, винта и шпильки выбирают в зависимости от толщины соединяемых деталей. Рассмотрим расчет на прочность резьбовых соединений при постоянной нагрузке. Болт нагружен внешней силой F (болт без предварительной затяжки), например, нарезанный участок крюка для подвешивания груза. Опасным является сечение крюка, ослабленное нарезкой (рис. 26.20). Из условия прочности на растяжение
откуда
где
Рис. 26.20. Крюковая подвеска
Болт затянут силой затяжки F з, а внешняя нагрузка отсутствует (ненагруженные крышки, кронштейны и т. п.). Стержень болта испытывает совместное действие растяжения и кручения, т. е. растягивается осевой силой F з от затяжки болта и скручивается моментом, равным моменту сил трения в резьбе T p (формула (26.5)), Прочность таких болтов (рис. 26.21) определяют по эквивалентному напряжению
где
Рис. 26.21. К расчету болта, нагруженного только силой затяжки
Для стандартных метрических резьб
Расчетный диаметр резьбы болта определяют по формуле (26.9), принимая F = F р.
Болтовое соединение нагружено силами, сдвигающими детали в стыке. Условием надежности соединения является отсутствие сдвига деталей в стыке. В соединении с зазором (рис. 26.22, а) болт устанавливают с предварительной затяжкой. Внешняя сила F непосредственно на болт не передается, поэтому его рассчитывают на растяжение по силе затяжки F з.

Рис. 26.22. К расчету болта, нагруженного поперечной силой: а – поставленного с зазором; б – без зазора Во избежание сдвига деталей при наличии зазора сила трения на поверхностях стыка должна быть не меньше внешней сдвигающей силы F:
где i – число стыков в соединении; f – коэффициент трения; K – коэффициент запаса (K = 1, 3–1, 5 при статической и K = z – число болтов в соединении. Болт в этом случае рассчитывают по силе затяжки:
При установке болта без зазора (рис. 26.22, б) предварительная затяжка не требуется. Болт испытывает срез и смятие. Стержень болта рассчитывают на срез, а при тонких деталях – и на смятие. Условия прочности
где d o – диаметр ненарезанной части болта;
S – наименьшая толщина детали. Болт затянут, а внешняя нагрузка стремится раскрыть стык (болты для крепления крышек резервуаров для газа и жидкости, нагруженные давлением выше атмосферного, крепления цилиндров, насосов, станин к фундаментам и др.). Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка (не допустить появления зазора) под нагрузкой. Эта задача решается с учетом деформации деталей соединения. Внешняя нагрузка
а б
Рис. 26.23. К расчету затянутого болта с учетом деформации и соединенных деталей
Суммарная нагрузка на затянутый болт
где Величина
где Из равенства (26.11) следует, что
Точный расчет коэффициента При приближенных расчетах принимают: – для соединений стальных и чугунных деталей без упругих прокладок – для соединения тех же деталей, но с упругими прокладками (резина, полиэтилен, асбест, паронит и др.) Предварительная затяжка болта F з должна быть больше минимальной силы предварительной затяжки болта:
Из условия сохранения плотности стыка соединяемых деталей (невозможности образования зазора) принимают
где K з – коэффициент запаса предварительной затяжки: при постоянной нагрузке K з = 1, 25–2, 0; при переменной K з = 2, 5–4. При расчете на прочность, если возможна последующая затяжка болта, его рассчитывают по расчетной нагрузке F р с учетом кручения:
26.5.6. Расчет резьбовых соединений при переменном режиме нагружения
Крепежные детали, работающие при переменном режиме нагружения, рассчитывают на усталость. Болты устанавливаются с предварительной затяжкой, при которой создается напряжение Расчет на усталость ведут как проверочный по двум коэффициентам запаса прочности: по амплитуде цикла и по наибольшему напряжению цикла (рис. 26.24). Предварительно болт рассчитывают из условия его статической прочности с учетом формул (26.10) или (26.12).
Рис. 26.24. Циклы переменных напряжений
Коэффициент запаса прочности по амплитуде цикла
где
Коэффициент запаса по наибольшему напряжению цикла
где При За счет уменьшения коэффициента внешней нагрузки может быть повышена прочность резьбового соединения при переменных нагрузках. Это может быть достигнуто уменьшением податливости стыка и увеличением податливости болта, в частности, диаметр стержня болта уменьшают до диаметра d 3. ЛИТЕРАТУРА
1. Аркуша, А.И. Руководство к решению задач по теоретической механике / А.И. Аркуша. – М.: Высш. школа, 1989; 1990; 1999. 2. Артоболевский, И.И. Теория механизмов и машин / И.И. Артоболевский. – М.: Машиностроение, 1975. – 639 с. 3. Артоболевский, И.И. Сборник задач по теории механизмов и машин / И.И. Артоболевский, Б.В. Эдельштейн. – М.: Машиностроение, 1975. – 256 с. 4. Беляев, Н.М. Сопротивление материалов / Н.М. Беляев. – М.: Наука, 1976. – 608 с. 5. Гернет, М.М. Курс теоретической механики / М.М. Гернет. – М.: Высшая школа, 1970.– 440 с. 6. Дубейковский, Е.Н. Сопротивление материалов: учебное пособие для машиностроительных специальностей техникумов / Е.Н. Дубейковский, Е.С. Савушкин. – М.: Высшая школа, 1985. –192 с. 7. Иосилевич, Г.Б. Прикладная механика: учеб. для вузов / Г.Б. Иосилевич, Г.Б. Строганов, Г.С. Маслов; под ред. Г.Б. Иосилевича. – М.: Высшая школа, 1989. – 360 с. 8. Ицкович, Г.М. Сборник задач по сопротивлению материалов: учебное пособие / Г.М. Ицкович, А.И. Винокуров, Н.В. Барановский. – 4-е изд. – Л.: Судостроение, 1972. 9. Каленик, В.В. Текст лекций по разделу «Теория механизмов и машин» курса «Прикладная механика» для студентов немеханических специальностей / В.В. Каленик, В.К. Акулич. – Минск: БПИ, 1983. 10. Кильчевский, Н.А. Основы теоретической механики / Н.А. Кильчевский, Н.И. Ремизова, Н.Н. Шепелевская. – Киев: Технiка, 1968. – 260 с. 11. Кинасошвили, Р.С. Сопротивление материалов / Р.С. Кинасошвили. – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1975. – 384 с. 12. Методические указания по решению задач по курсу «Прикладная механика» для студентов немеханических специальностей: в 2 ч. / А.А. Миклашевич [и др.]. – Минск: БПИ, 1985. – Ч 2. – 37 с. 13. Мовкин, М.С. Теоретическая механика / М.С. Мовкин, А.Б. Израелит. – Л.: Судостроение, 1972. 14. Никитин, Е.М. Теоретическая механика для техникумов / Е.М. Никитин. – М.: Наука, 1971 (и последующие издания). 15. Осадчий, В. И. Руководство к решению задач по теоретической механике / В.И. Осадчий, А.М. Фаин. – М.: Высш. школа, 1972. 16. Павловский, М.А. Теоретическая механика: в 2 ч. / М.А. Павловский, Л.Ю. Акинфеева, О.Ф. Бойчук. – Киев: Вища школа, 1989; 1990. – 350 с. 17. Подскребко, М.Д. Задания по расчетно-графическим работам курса «Прикладная механика»: в 2 ч. / М.Д. Подскребко, С.С. Томило, А.Н. Шинкевич. – Минск: БИМСХ, 1990. – Ч. 1. – 59 с. 18. Пособие к решению задач по сопротивлению материалов: учеб. пособие для техн. вузов / И.М. Миролюбов [и др.]. – 19. Прикладная механика: методические указания и контрольные задания для студентов-заочников / под ред. П.Г. Гузенкова. – М.: Машиностроение, 1982. – 112 с. 20. Прикладная механика: учеб. пособие/ А.Т. Скойбеда [и др.]; под общ. ред. А.Т. Скойбеды. – Минск: Вышэйшая школа, 1997. – 552 с. 21. Руденок, Е.Н. Техническая механика: сб. заданий: учеб. пособие / Е.Н. Руденок, В.П. Соколовская. – Минск: Высшая школа, 1990. – 238 с. 22. Сборник задач по сопротивлению материалов / под ред. В.К. Качурина. – М.: Наука, 1970. – 432 с. 23. Сборник задач по технической механике / В.В. Багреёв [и др.]. – Л.: Судостроение, 1968. 24. Соколов, Б.Ф. Методические указания к семестровым заданиям по объединенному курсу «Теоретическая и прикладная механика» / Б.Ф. Соколов [и др.]. – Челябинск: Челябинский ин-т механизации и электрификации сельского хозяйства, 1985. 25. Феодосьев, В.И. Сопротивление материалов / В.И. Феодосьев. – М.: Наука, 1986. – 512 с. 26. Феодосьев, В. И. Избранные задачи и вопросы по сопротивлению материалов / В.И. Феодосьев. – 4-е изд., испр. и доп. – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1973. – 400 с. 27. Шапиро, Д.М. Сборник задач по сопротивлению материалов: учебное пособие для машиностроительных техникумов / Д.М. Шапиро, А.И. Подорванова, А.Н. Миронов. – 3-е изд., перераб. – М.: Высшая школа, 1970. 28. Юдин, В.А. Теория механизмов и машин / В.А. Юдин, Л.В. Петрокас. – М.: Машиност
|




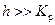 ).
). ; для склеивания –
; для склеивания –  .
.
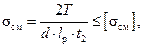 (26.4)
(26.4)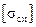 –допускаемое напряжение на смятие.
–допускаемое напряжение на смятие.
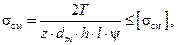



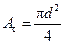 – площадь штифта при срезе;
– площадь штифта при срезе;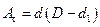 – площадь поверхности смятия (сжатия);
– площадь поверхности смятия (сжатия);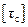 = 70–80 МПа – допускаемое напряжение при срезе;
= 70–80 МПа – допускаемое напряжение при срезе;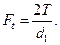

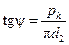 ;
;


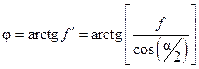 – приведенный угол трения;
– приведенный угол трения; – приведенный коэффициент трения в резьбе;
– приведенный коэффициент трения в резьбе;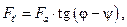
 – окружная сила при отвинчивании гайки.
– окружная сила при отвинчивании гайки. (26.5)
(26.5)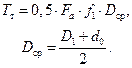
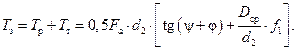 (26.6)
(26.6)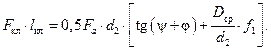 (26.7)
(26.7)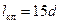 для метрических резьб можно принять: ψ = 2, 5°;
для метрических резьб можно принять: ψ = 2, 5°;  ;
; 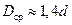 ;
;  . Из анализа формулы (26.7) следует, что обычно
. Из анализа формулы (26.7) следует, что обычно 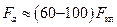 . Таким образом, сила в 1 H, приложенная на конце ключа, создает силу прижатия деталей 60–100 Н. Такой выигрыш в силе обеспечивает легкость сборки соединения.
. Таким образом, сила в 1 H, приложенная на конце ключа, создает силу прижатия деталей 60–100 Н. Такой выигрыш в силе обеспечивает легкость сборки соединения. или
или  , то резьба будет самотормозящейся. Условие самоторможения:
, то резьба будет самотормозящейся. Условие самоторможения:
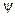 = 2°30'–3°30', а приведенный угол трения φ изменяется в зависимости от коэффициента трения в пределах от 6° (при
= 2°30'–3°30', а приведенный угол трения φ изменяется в зависимости от коэффициента трения в пределах от 6° (при  ) до 11° (при
) до 11° (при 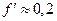 ). Таким образом, все крепежные резьбы – самотормозящиеся. Это объясняет важное преимущество крепежной резьбы – надежное стопорение гайки (винта) в любом положении. Однако это свойство проявляется главным образом при статических нагрузках. При переменных нагрузках условие самоторможения не соблюдается. Поэтому необходимо стопорение резьбовых соединений.
). Таким образом, все крепежные резьбы – самотормозящиеся. Это объясняет важное преимущество крепежной резьбы – надежное стопорение гайки (винта) в любом положении. Однако это свойство проявляется главным образом при статических нагрузках. При переменных нагрузках условие самоторможения не соблюдается. Поэтому необходимо стопорение резьбовых соединений. , где T з находят по формуле (26.6), а
, где T з находят по формуле (26.6), а  – по той же формуле, но без учета сил трения (f 1 = 0, φ = 0). Для собственно винтовой пары (Т т = 0)
– по той же формуле, но без учета сил трения (f 1 = 0, φ = 0). Для собственно винтовой пары (Т т = 0)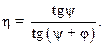
 ; т. к. большинство винтовых механизмов самотормозящиеся, их КПД меньше 0, 5.
; т. к. большинство винтовых механизмов самотормозящиеся, их КПД меньше 0, 5. (26.8)
(26.8)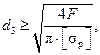 (26.9)
(26.9)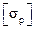 = 0, 6
= 0, 6  – допускаемое напряжение при растяжении болта из углеродистой стали.
– допускаемое напряжение при растяжении болта из углеродистой стали.

 – напряжение от растяжения, определяемое по формуле (26.8) при F = F з;
– напряжение от растяжения, определяемое по формуле (26.8) при F = F з; – напряжение от кручения:
– напряжение от кручения: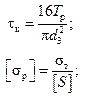
 – требуемый коэффициент запаса прочности болта, принимаемый в зависимости от материала болта, характера нагрузки и диаметра болта.
– требуемый коэффициент запаса прочности болта, принимаемый в зависимости от материала болта, характера нагрузки и диаметра болта.
 , т. е. расчет болта на совместное действие растяжения и кручения можно заменить расчетом на растяжение, но по увеличенной в 1, 3 раза силе F р. Для метрических резьб
, т. е. расчет болта на совместное действие растяжения и кручения можно заменить расчетом на растяжение, но по увеличенной в 1, 3 раза силе F р. Для метрических резьб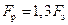 .
.


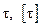 – соответственно расчетное и допускаемое напряжения для материала болта на срез,
– соответственно расчетное и допускаемое напряжения для материала болта на срез, 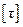 = (0, 2–0, 3)
= (0, 2–0, 3) 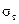 ;
; – соответственно расчетное и наименьшее допускаемое напряжения смятия (для материала болта или детали),
– соответственно расчетное и наименьшее допускаемое напряжения смятия (для материала болта или детали),  (R – равнодействующая нагрузки; z – число болтов) вызывает удлинение болта на
(R – равнодействующая нагрузки; z – число болтов) вызывает удлинение болта на 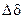 (рис. 26.23), а деформация деталей уменьшается на ту же величину. Нагрузка со стороны деталей на болт также уменьшится. Именно поэтому считают, что болт воспринимает часть внешней нагрузки
(рис. 26.23), а деформация деталей уменьшается на ту же величину. Нагрузка со стороны деталей на болт также уменьшится. Именно поэтому считают, что болт воспринимает часть внешней нагрузки 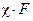 .
.

 (26.10)
(26.10)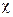 –коэффициент внешней нагрузки, показывающий, какая часть внешней нагрузки воспринимается болтом (учитывает податливость болта и соединяемых деталей).
–коэффициент внешней нагрузки, показывающий, какая часть внешней нагрузки воспринимается болтом (учитывает податливость болта и соединяемых деталей).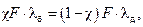 (26.11)
(26.11) – коэффициенты податливости соответственно болта и деталей, численно равные изменению их длины при действии силы, равной 1 H.
– коэффициенты податливости соответственно болта и деталей, численно равные изменению их длины при действии силы, равной 1 H.
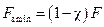 .
.
 (26.12)
(26.12)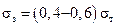 . Вследствие этого циклическое изменение расчетной силы F б значительно меньше по сравнению с изменением внешней силы F.
. Вследствие этого циклическое изменение расчетной силы F б значительно меньше по сравнению с изменением внешней силы F.

 – предел выносливости материала болта (шпильки);
– предел выносливости материала болта (шпильки);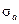 – амплитуда переменных напряжений:
– амплитуда переменных напряжений: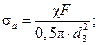
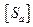 – требуемый коэффициент запаса прочности по амплитуде
– требуемый коэффициент запаса прочности по амплитуде 



