Решение. 1. Определение передаточного отношения механизма
1. Определение передаточного отношения механизма.
Выделим из механизма ступень с неподвижными осями, состоящую из колес z 1, z 2, z 2´ , z 3 , z 3´ , z 4, и планетарную ступень, состоящую из колес z 4´ , z 5, z 5´ , z 6 и водила Н (7); а) для ступени с неподвижными осями
оси колес 1 и 4 непараллельные, поэтому знак передаточного отношения не определяем, а покажем направления вращения колес неподвижной ступени в соответствии с правилом стрелок:
б) чтобы определить передаточное отношение планетарной ступени, используем формулу Виллиса; остановим водило Н (7), используя зависимость (15.3), получим
колесо 6 неподвижно (
в) передаточное отношение всего механизма
Передаточное отношение планетарной ступени Покажем направление угловой скорости 2. Угловая скорость и угловое ускорение ведомого звена 7 по модулю:
3. Определить время, в течение которого угловая скорость увеличивается вдвое: Для ускоренного вращения Отсюда 4. Для расчета момента инерции
С учетом сказанного масса определяется по формуле
где ρ – плотность, ρ = 8000 кг/м3 (по условию).
Вес колеса
Смещение центра масс (точка А на рис. 15.11) l = 2 мм = 0, 002 м. Нормальная составляющая силы инерции
Нормальное ускорение точки A
Касательное ускорение точки A и касательная составляющая силы инерции:
Определим полное ускорение точки А, силу инерции и направление силы инерции:
В практических расчетах составляющей
Силой веса по сравнению с силой инерции при практических расчетах также можно пренебречь. Момент сил инерции
Покажем направление всех векторных величин на чертеже. 5. Определение общего КПД механизма.
Здесь
РАЗДЕЛ 3 ОСНОВЫ РАСЧЕТОВ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
Глава 16. Напряженно-деформированное СОСТОЯНИЕ детали
16.1. Метод сечений
Под внутренними силами будем подразумевать не их абсолютные значения, а только те приращения, которые вызваны действующими на тело нагрузками, Для расчета на прочность необходимо иметь возможность определять внутренние силы по заданным внешним силам. Основу для решения этой задачи дает метод сечений «Розу»: Р – разрезаем тело плоскостью на две части; О – отбрасываем одну часть; З – заменяем действие отброшенной части внутренними силами; У – уравновешиваем оставшуюся часть и из уравнения равновесия определяем внутренние силы. Применяя метод сечений, силы, являющиеся внутренними для тела в целом, переводят во внешние для одной из его частей, полученной в результате мысленно проведенного сечения. Рассмотрим брус, находящийся в равновесии под действием произвольной системы внешних (активных и реактивных) сил (рис. 16.1). Рассечем его на две части (I и II) некоторой произвольной плоскостью, перпендикулярной его продольной оси, и отбросим одну из частей (например I) (рис. 16.2). Из теоретической механики известно, что любая система сил может быть приведена к ее главному вектору и главному моменту, которые статически эквивалентны заданной системе сил. Главный вектор системы – три составляющие по осям выбранной системы координат. Главный момент – три момента, каждый из которых стремится повернуть тело вокруг одной из координатных осей. Составляющие главного вектора и главного момента внутренних сил, возникающих в поперечном сечении бруса (рис. 16.3), носят название внутренних силовых факторов (ВСФ) в этом сечении. Nz – продольная (или нормальная) сила; Qx, Qy – поперечные силы; Mz – крутящий момент; Qx, Qy – изгибающие моменты (рис. 16.4).
Имеют место следующие виды деформаций: если если
Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на продольную ось OZ бруса всех внешних сил, приложенных к его оставленной части.
16.2. Напряжение как мера внутренних сил
Для суждения об интенсивности внутренних сил в определенной точке данного сечения введено понятие о напряжении. Выделим в окрестности интересующей нас точки сечения малую площадку площадью
Рис. 16.5. Элементарная сила в точке сечения Истинное напряжение в данной точке рассматриваемого сечения
Отношение будет величиной конечной. Напряжение в данной точке по рассматриваемому сечению есть величина векторная (вектор Единица измерения напряжения – паскаль (Па). Паскаль – это напряжение, при котором на площадке в 1 м2 возникает внутренняя сила, равная 1 H; но эта единица очень мала, поэтому используется кратная ей единица – мегапаскаль, 1 МПа = 106 Па. Разложим вектор напряжения р на две составляющие: одну – направленную по нормали к сечению (нормальное напряжение
В ряде случаев оказывается удобным разложить вектор р не на две, а на три составляющие, направленные параллельно координатным осям (рис. 16.7):
Правило индексов: первый индекс указывает, какой оси параллельна нормаль к площадке действия рассматриваемого напряжения, второй индекс показывает, какой оси параллельно данное напряжение. Установим связь между напряжениями и внутренними силовыми факторами в поперечном сечении бруса. Элементарные внутренние силы:
Выражения составляющих главного вектора внутренних сил:
Умножая каждую из элементарных сил на расстояние до соответствующей оси, получаем элементарные моменты внутренних сил:
Суммируя элементарные моменты по всей площади сечения, получаем выражения для составляющих главного момента внутренних сил:
Выражения (16.1)–(16.6) не служат для вычисления внутренних силовых факторов. Они выражают их физическую сущность.
Глава 17. Напряженно-деформированное состояние элементарного объема материала 17.1. Напряженное состояние в точке. Закон парности касательных напряжений. Главные площадки и главные напряжения. Классификация напряженных состояний Напряженное состояние в данной точке тела характеризуется совокупностью нормальных и касательных напряжений, возникающих на бесчисленном множестве различно ориентированных в пространстве площадок, которые можно провести через эту точку. Предположим, что в окрестности исследуемой точки выделен бесконечно малый элемент, имеющий форму прямоугольного параллелепипеда, и напряжения, возникающие на его гранях, известны. Девять величин называют компонентами (рис. 17.1) напряженного состояния в данной точке. Из условия равновесия выделенного элемента следует, что составляющие касательных напряжений, возникающих на любых двух взаимно перпендикулярных площадках, перпендикулярные общему ребру этих площадок, равны по абсолютному значению, т. е.
Рис. 17.1. Напряжения на гранях элементарного куба
Это положение называют законом парности касательных напряжений. Следовательно, из девяти компонентов напряженного состояния независимы лишь шесть. Первое положение теории напряженного состояния может быть сформулировано следующим образом: напряженное состояние в точке тела задано, если известны напряжения на любых трех проходящих через нее взаимно перпендикулярных площадках. Среди бесчисленного множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называют главными. Классификацию видов напряженного состояния ведут по главным напряжениям. Если все три главных напряжения отличны от нуля, напряженное состояние называют объемным, пространственным или трехосным. В случае если одно из главных напряжений равно нулю, напряженное состояние называют плоским, или двухосным, наконец, если лишь одно из главных напряжений отлично от нуля, напряженное состояние линейное, или одноосное:
Элементы, выделенные главными площадками, для различных частных случаев напряженного состояния показаны на рис. 17.2: а – трехосное растяжение; б – трехосное сжатие; в – трехосное смешанное напряженное состояние; г – двухосное растяжение; д – двухосное сжатие; е – частный случай двухосного смешанного напряженного состояния – чистый сдвиг; ж – одноосное растяжение; з – одноосное сжатие. Площадки, свободные от напряжений, так называемые нулевые главные площадки, покрыты точками.

Рис. 17.2. Различные случаи напряженного состояния 17.2. Однородное растяжение бруса как пример реализации одноосного напряженного состояния материала
При растяжении (сжатии) прямого бруса в его поперечных сечениях возникает только один внутренний силовой фактор – продольная сила, обозначаемая Nz или N (рис. 17.3, 17.4).

Рис. 17.3. Однородное сжатие бруса

Рис. 17.4. Однородное растяжение бруса
Прямые брусья, работающие на растяжение или сжатие, часто называют стержнями. Продольные силы, соответствующие деформации растяжения, условимся считать положительными, а сжатия – отрицательными. При растяжении продольная сила направлена от сечения (рис. 17.4, б), а при сжатии – к сечению (рис. 17.3, а). Модуль и направление (знак) продольной силы определяются из уравнения равновесия, составленного для отсеченной (оставленной после проведения сечения) части бруса:
откуда
Продольной силой в поперечном сечении бруса называется равнодействующая внутренних нормальных сил, возникающих в этом сечении:
В тех случаях когда продольные силы в различных поперечных сечениях бруса неодинаковы, закон их изменения по длине бруса удобно представить в виде графика, называемого эпюрой продольных сил. Эпюра продольных сил – это график функции Эпюру продольных сил строят в первую очередь для того, чтобы использовать ее при расчете бруса на прочность. Напряжения. При растяжении (сжатии) бруса в его поперечных сечениях возникают только нормальные напряжения (рис. 17.5):
При растяжении напряжения считают положительными. В местах резкого изменения формы и размеров поперечного сечения бруса также возникают местные напряжения (рис. 17.6). Это явление называют концентрацией напряжений. В тех случаях когда нормальные напряжения в различных поперечных сечениях бруса неодинаковы, целесообразно показывать закон их изменения по длине бруса в виде графика – эпюры нормальных напряжений.
17.3. Продольная и поперечная деформации. Закон Гука. Модуль упругости. Коэффициент Пуассона
Вопрос об определении нормальных напряжений теснейшим образом связан с расчетами бруса на прочность. Умение вычислять деформации и перемещения необходимо для расчетов на жесткость, а также для определения сил в статически неопределимых системах. Выделим из бруса, изображенного на рис. 17.7, бесконечно малый элемент длиной d z.
Рис. 17.7. К определению продольных и поперечных деформаций бруса при его растяжении
Отношение приращения (изменения) длины элемента к его первоначальной длине называется относительным удлинением или продольной деформацией:
Очевидно, продольная деформация – безразмерная величина. В некоторых случаях ее выражают в процентах. При растяжении продольную деформацию считают положительной, а при сжатии – отрицательной. Отношение изменения
Продольную и поперечную деформации называют также линейными деформациями. В известных пределах нагружения между
Коэффициент пропорциональности E называют модулем продольной упругости (модуль упругости 1-го рода; модуль Юнга). Модуль продольной упругости – физическая постоянная данного материала, характеризующая его жесткость: чем жестче материал, тем меньше он деформируется при данном напряжении. Опытным путем установлено, что при простом растяжении или сжатии отношение поперечной деформации к продольной – величина постоянная для данного материала. Это отношение, взятое по абсолютному значению, называется коэффициентом поперечной деформации, или коэффициентом Пуассона:
Значения коэффициента Пуассона для различных материалов находятся в пределах от 0 до 0, 5. Минимальное значение коэффициент Пуассона имеет для пробки ( Определение изменения длины (удлинения или укорочения) бруса. Удлинение или укорочение равно
Выражение (17.1) часто называют формулой Гука, а произведение Е ∙ А условно называют жесткостью сечения бруса при растяжении (сжатии). Жесткость бруса (участка бруса) определяется по формуле
и численно равна силе, вызывающей удлинение (или укорочение) бруса, равное единице длины: 1 м или 1 см и т. п. При расчетах в единицах СИ коэффициент жесткости выражают в ньютонах на метр (Н/м). Величину, обратную коэффициенту жесткости, называют коэффициентом податливости:
Коэффициент податливости численно равен удлинению (укорочению) бруса, вызванному силой, равной единице силы: 1 H или 1 кН:
или
17.4. Частный случай плоского напряженного состояния – чистый сдвиг. Закон Гука при сдвиге
Рассмотрим частный случай плоского напряженного состояния, для которого отличные от нуля главные напряжения равны по модулю и противоположны по знаку (рис. 17.8).
Рис. 17.8. Частный случай плоского напряженного состояния
Такое напряженное состояние носит название чистого сдвига. Максимальное главное напряжение следует обозначить Чистым сдвигом называют такое плоское напряженное состояние, при котором в окрестности данной точки можно выделить элемент таким образом, чтобы на четырех его гранях были только равные между собой касательные напряжения. В качестве примера, иллюстрирующего возникновение чистого сдвига, рассмотрим кручение тонкостенной трубы (рис. 17.9, а). Из условия равновесия отсеченной части трубы, изображенной отдельно на рис. 17.9, б, следует, что в поперечном сечении (любом) возникает лишь один внутренний силовой фактор – крутящий момент Mz, численно равный внешнему моменту М. В поперечном сечении трубы возникают касательные напряжения Деформация сдвига. Изобразим элемент, выделенный площадками, на которых возникают только касательные напряжения (рис. 17.10). Учитывая, что нас интересуют деформации элемента, а не его перемещения как твердого тела, одну из граней будем считать неподвижной. Мерой деформации сдвига служит изменение первоначального прямого угла между гранями элемента, называемое углом сдвига и обозначаемое
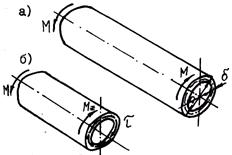
Рис. 17.9. Кручение тонкостенной трубы
Рис. 17.10. Деформация элемента при сдвиге
Между углом сдвига и соответствующим касательным напряжением существует прямая пропорциональность – закон Гука при сдвиге:
Здесь G – упругая постоянная материала, характеризующая его жесткость при деформации сдвига и называемая модулем сдвига или модулем упругости 2-го рода:
Размерность модуля сдвига та же, что и напряжения. Глава 18. Механические свойства конструкционных материалов
18.1. Экспериментальные исследования механических свойств при проведении стандартных испытаний на растяжение
Основные механические характеристики. 1. Прочность – способность материала не разрушаясь воспринимать внешние механические воздействия. 2. Пластичность – способность материала не разрушаясь давать значительные остаточные деформации. 3. Упругость – способность материала после снятия нагрузок восстанавливать свои первоначальные формы и размеры. 4. Твердость – способность материала сопротивляться проникновению в него другого тела, практически не получающего остаточных деформаций. По характеру нагружения различают испытания статические, динамические и испытания на усталость (при переменных напряжениях). По виду деформации различают испытания на растяжение, сжатие, срез, кручение, изгиб. Реже проводят испытания при сложном нагружении, например на совместное действие изгиба и кручения. Механические испытания проводят на образцах, формы и размеры которых установлены государственными стандартами или техническими условиями (рис. 18.1).
Рис. 18.1. Образец для проведения испытаний
Статические испытания на растяжение. Наиболее распространенным является испытание на растяжение статической нагрузкой. Испытания проводят на разрывных или универсальных машинах с механическим или гидравлическим силообразованием. Машина снабжена диаграммным аппаратом, который в процессе испытания вычерчивает график зависимости между силой F, растягивающей образец, и соответствующим удлинением
а
б
Рис. 18.2. График зависимости F (Δ l) (а) при растягивании образца (б)
Для получения механических характеристик материала (т. е. для того, чтобы исключить влияние абсолютных размеров образца) эту диаграмму перестраивают: все ординаты делят на начальную площадь поперечного сечения А 0, а все абсциссы – на начальную расчетную длину l 0. В результате получают так называемую условную диаграмму растяжения (рис. 18.3).
Рис. 18.3. Диаграмма растяжения образца
На рис. 18.3
18.2. Условие прочности, коэффициент запаса прочности, допускаемые напряжения
Конструкционные материалы можно разделить на три основные группы: пластичные, хрупкопластичные, хрупкие. Механические испытания материалов позволяют определить те напряжения, при которых образец из данного материала разрушается или в нем возникают заметные пластические деформации. Эти напряжения называют предельными (или опасными). Отношение предельного напряжения
Значение n должно быть больше единицы (n > 1), иначе прочность конструкции будет нарушена. Устанавливают значение минимально необходимого коэффициента запаса прочности. Этот коэффициент обозначают [ n ] и называют требуемым (или нормативным) коэффициентом запаса прочности. Прочность элемента конструкции считают обеспеченной, если его расчетный коэффициент запаса прочности не ниже требуемого, т. е.
Это неравенство называют условием прочности. Используя выражение (18.1), перепишем условие прочности в виде
Отсюда можно получить и такую форму записи условия прочности:
Правую часть последнего неравенства называют допускаемым напряжением и обозначают
В случае, если предельные, а следовательно, и допускаемые напряжения при растяжении и сжатии различны, их обозначают соответственно Пользуясь понятием «допускаемое напряжение», можно сказать, что прочность конструкции обеспечена, если возникающее в ней наибольшее напряжение не превышает допускаемого, т. е.
Это неравенство, так же как и неравенства (18.2) и (18.3), называют условием прочности. Будут встречаться три упоминавшиеся уже категории напряжений. 1. Предельные (или опасные) напряжения, при достижении которых появляются признаки непосредственного разрушения или возникают пластические деформации. Эти напряжения зависят от свойств материалов и вида деформации, например, для серого чугуна предельное напряжение (предел текучести) при сжатии 2. Допускаемые напряжения – наибольшие напряжения, которые можно допустить в рассчитываемой конструкции из условий ее безопасной, надежной и долговечной работы. Эти напряжения зависят от свойств материала, вида деформации и требуемого (принятого или заданного) коэффициента запаса прочности. 3. Расчетные напряжения – напряжения, которые возникают в элементе конструкции под действием приложенных к нему нагрузок. Эти напряжения зависят от нагрузок, действующих на элемент конструкции, и его размеров. Глава 19. Расчет несущей способности типовых элементов, моделируемых в форме стержня
19.1. Расчеты на прочность стержней при растяжении–сжатии
Условие прочности при растяжении–сжатии записывается в виде
Под Незначительное превышение наибольших расчетных напряжений над допускаемыми, конечно, не опасно, так как допускаемое напряжение составляет лишь некоторую часть от предельного, обычно до 3 %. В зависимости от цели расчета (постановки задачи) различают три вида расчетов на прочность: 1) проверочный; 2) проектный; 3) определение допускаемой нагрузки. 1. При проверочном расчете нагрузка бруса, его материал (а следовательно, допускаемое Расчетная формула (условие прочности при растяжении или сжатии) имеет вид
где N – продольная сила в указанном сечении; A – площадь опасного поперечного сечения;
В ряде случаев при проверочном расчете удобнее сопоставлять не расчетное напряжение с допускаемым, а сравнивать расчетный коэффициент запаса прочности для опасного сечения с требуемым, т. е. проверять, соблюдается ли неравенство
2. При проектном расчете нагрузки
|





 = 0), используя зависимость (15.4), получим
= 0), используя зависимость (15.4), получим

 . Следовательно, водило Н (7) вращается в ту же сторону, что и колесо 4.
. Следовательно, водило Н (7) вращается в ту же сторону, что и колесо 4. и углового ускорения
и углового ускорения  на чертеже стрелками. Поскольку
на чертеже стрелками. Поскольку  , вращение ускоренное.
, вращение ускоренное.


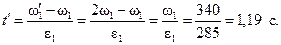
 коническое ведущее колесо со средним модулем mm = 2 мм, z 1 = 18 заменим цилиндром с диаметром, равным среднему делительному диаметру:
коническое ведущее колесо со средним модулем mm = 2 мм, z 1 = 18 заменим цилиндром с диаметром, равным среднему делительному диаметру:
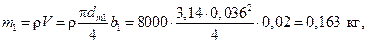







 , как малой величиной, можно пренебречь и считать, что
, как малой величиной, можно пренебречь и считать, что  Сравним силу тяжести и силу инерции:
Сравним силу тяжести и силу инерции:


 – КПД конической пары с учетом потерь в подшипниках.
– КПД конической пары с учетом потерь в подшипниках. – КПД цилиндрической пары (две пары по условию);
– КПД цилиндрической пары (две пары по условию); – КПД планетарной передачи.
– КПД планетарной передачи.
 Рис. 16.1. Внешние силы
Рис. 16.1. Внешние силы
 Рис. 16.2. Внутренние силы
Рис. 16.2. Внутренние силы
 Рис. 16.3. Метод сечений
Рис. 16.3. Метод сечений
 Рис. 16.4. Внутренние силы
в произвольном сечении бруса
Рис. 16.4. Внутренние силы
в произвольном сечении бруса
 – растяжение,
– растяжение,  или
или 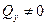 – срез;
– срез; – кручение,
– кручение,  или
или  – изгиб.
– изгиб. Для определения каждого из внутренних силовых факторов надо составить соответствующее уравнение равновесия для всех сил, действующих на оставленную часть бруса (см. рис. 16.4).
Для определения каждого из внутренних силовых факторов надо составить соответствующее уравнение равновесия для всех сил, действующих на оставленную часть бруса (см. рис. 16.4).
 ; допустим, что на этой площадке возникает внутренняя сила
; допустим, что на этой площадке возникает внутренняя сила  (рис. 16.5). Отношение этой внутренней силы к площади выделенной площадки называется средним напряжением
(рис. 16.5). Отношение этой внутренней силы к площади выделенной площадки называется средним напряжением  в окрестности рассматриваемой точки по проведенному сечению (на площадке
в окрестности рассматриваемой точки по проведенному сечению (на площадке 


 ), вторую – лежащую в плоскости сечения (касательное напряжение
), вторую – лежащую в плоскости сечения (касательное напряжение  ) (рис. 16.6). Между напряжениями р,
) (рис. 16.6). Между напряжениями р, 
 Рис. 16.6. Полное р, нормальное σ
и касательное τ напряжения в точке
Рис. 16.6. Полное р, нормальное σ
и касательное τ напряжения в точке
 Рис. 16.7. Внутренние напряжения
Рис. 16.7. Внутренние напряжения
 .
. ;
; ;
; .
. ; (16.1)
; (16.1) ; (16.2)
; (16.2) . (16.3)
. (16.3) ;
; ;
; .
. ; (16.4)
; (16.4) ; (16.5)
; (16.5) . (16.6)
. (16.6)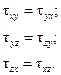

 –объемное состояние;
–объемное состояние; – плоское;
– плоское; – линейное.
– линейное.



 .
.

 Рис. 17.5. Нормальные напряжения
Рис. 17.5. Нормальные напряжения
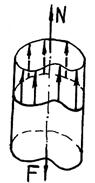 Рис. 17.6. Местные напряжения
Рис. 17.6. Местные напряжения


 размера поперечного сечения к его первоначальному значению называют относительным поперечным сужением (расширением), или поперечной деформацией:
размера поперечного сечения к его первоначальному значению называют относительным поперечным сужением (расширением), или поперечной деформацией:
 (деформацией) и соответствующим (действующим в ее направлении)
(деформацией) и соответствующим (действующим в ее направлении) 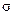 напряжением существует прямо пропорциональная (линейная) зависимость, которая носит название закона Гука и записывается в виде
напряжением существует прямо пропорциональная (линейная) зависимость, которая носит название закона Гука и записывается в виде

 = 0); максимальное – для каучука (
= 0); максимальное – для каучука ( 0, 5). Для большинства металлов и сплавов значение коэффициента Пуассона колеблется в сравнительно узких пределах: от 0, 23 до 0, 35 (в среднем примерно 0, 3).
0, 5). Для большинства металлов и сплавов значение коэффициента Пуассона колеблется в сравнительно узких пределах: от 0, 23 до 0, 35 (в среднем примерно 0, 3). (17.1)
(17.1)




 , минимальное
, минимальное  ; по условию
; по условию  ; промежуточное главное напряжение
; промежуточное главное напряжение  = 0.
= 0. . Угол сдвига, выражается в радианах.
. Угол сдвига, выражается в радианах.
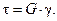


 (рис. 18.2).
(рис. 18.2).


 – предел пропорциональности – наибольшее напряжение, до достижения которого справедлив закон Гука;
– предел пропорциональности – наибольшее напряжение, до достижения которого справедлив закон Гука; – предел упругости – наибольшее напряжение, до достижения которого в образце не возникает остаточных деформаций;
– предел упругости – наибольшее напряжение, до достижения которого в образце не возникает остаточных деформаций; – предел текучести – напряжение, при котором происходит рост пластических деформаций образца при практически постоянной нагрузке;
– предел текучести – напряжение, при котором происходит рост пластических деформаций образца при практически постоянной нагрузке; – предел прочности (или временное сопротивление) – условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом до разрушения.
– предел прочности (или временное сопротивление) – условное напряжение, соответствующее наибольшей нагрузке, выдерживаемой образцом до разрушения. к наибольшему расчетному напряжению
к наибольшему расчетному напряжению  (18.1)
(18.1)
 (18.2)
(18.2) (18.3)
(18.3) .
.
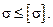
 примерно в четыре раза выше предельного напряжения при растяжении
примерно в четыре раза выше предельного напряжения при растяжении 
 или
или 
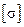 или предельное напряжение
или предельное напряжение 
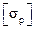 при растяжении и
при растяжении и  при сжатии).
при сжатии).


