Примеры решения задач. Задача-пример 1. На тележке массой 20 кг лежит груз массой 5 кг
Задача-пример 1. На тележке массой 20 кг лежит груз массой 5 кг. К грузу приложена сила F, сообщающая тележке с грузом ускорение а. Сила действует под углом 300 к горизонту. Каково максимальное значение этой силы, при котором груз не будет скользить по тележке? Коэффициент трения между грузом и тележкой 0, 20. Трением между тележкой и дорогой пренебречь. С каким ускорением будет двигаться тележка под действием силы F?
Прежде всего, по условию задачи сделаем рисунок, указав на нем некоторые данные и искомые величины. Далее необходимо проанализировать заданную ситуацию. Ясно, что в задаче рассматривается движение двух тел: груза и тележки. Причем возможны два варианта их движения: 1) оба тела движутся вместе, тогда ускорения их равны Для этого необходимо указать все силы, действующие отдельно на груз и на тележку, и выбрать те из них, которые имеют направление (или составляющую) вдоль направления ускорения. Итак, груз приобретает ускорение
находим эти проекции на направление ускорения и получаем скалярное равенство в виде: m2 × а2 = F× cosa – Fтр2 (1). С другой стороны, в направлении вертикальной оси движение груза не меняется, а значит силы, действующие вдоль него, скомпенсированы, т.е. сумма проекций этих сил на данное направление равна нулю:
F× sina + N2 – m2g = 0 (2). Методическое указание. Приведенная логика рассуждений отличается от общепринятого универсального способа тем, что при рассмотрении выбранного направления заранее отбрасываются силы, имеющие на него нулевые проекции. Более общая логика состоит в записи второго закона в форме 3 и последующем проектировании его на нужные направления. Автор ни сколько не умаляет достоинств таких действий (простота в использовании, универсальность и пр.), но предостерегает от привычки действовать «по шаблону», не вникая в физические взаимосвязи и не проявляя гибкости мышления! Приводимые в качестве примера рассуждения демонстрируют взаимосвязь теории с практикой, т.е. раскрывают сущность сил, как причин изменения движения тел.
Таким образом, получены два равенства из рассмотрения движения груза. Перейдем теперь к тележке. Под действием какой силы тележка движется с ускорением??? Как видно из рисунка, где указаны все действующие на нее силы, такой силой является сила трения. Методическое указание. Важно обратить особое внимание на двоякую роль силы трения при движении: 1-я – оказывает сопротивление движению (помеха) и 2-я – оказывается причиной (источник) движения. Поэтому каждый раз необходимо заново анализировать ситуацию с целью распознать, какова же роль трения в этом случае.
Учитывая третий закон Ньютона, приходим к выводу, что Fтр.2 = Fтр.1 = Fтр. (методическое требование: равные по модулю величины следует обозначать одинаково!). Второй закон Ньютона для тележки запишем в форме 1:
вектор справа равен вектору слева, значит равны модули этих векторов и можно опустить значки вектора: m1× a1 = Fтр.1 (3). Методическое указание. Определять силу N чаще всего приходится с целью последующего нахождения значения силы трения скольжения. Поэтому там, где силу трения не учитывают и не требуется специально определить реакцию опоры, вертикальное направление (а значит и вся совокупность сил, действующих в этом направлении) не рассматривается.
В вертикальном направлении на тележку действуют 3 силы: сила реакции дороги, сила тяжести и вес лежащего на ней груза. Заметим, что После того, как проделали анализ движения рассмотренных тел, переходим к нахождения искомых величин.
Будем искать максимальное значение силы Fmax, при котором груз все еще остается неподвижным относительно тележки (нет скольжения). Тогда а1=а2=а и равенства (1) и (3) запишутся в виде: m2 × а =F× cosa – Fтр (1а). m1× a =Fтр (3а). Складывая их почленно получаем запись второго закона Ньютона для системы «груз-тележка» (как единого целого!) в проекции на ось х: (m1 + m2) × а = F× cosa (4). Анализируя взаимозависимости между величинами, участвующими в этих равенствах, видим, что при увеличении силы F увеличивается общее ускорение системы а, т.е. увеличивается ускорение, в частности, тележки, а стало быть возрастает сила трения, действующая на тележку (причина ее ускорения). Но этот процесс обрывается по достижении силой трения своего максимального значения Fтр.ск. при величине внешней силы F = Fmax. Тогда учтем сразу, что Fтр.ск. = m× N2, где из (2) находим: N2 = m2g – Fmax× sina, получим: Fтр.ск. = m× (m2g – Fmax× sina), далее из (3а): аmax = Fтр.ск. /m1 =m× (m2g – Fmax× sina)/m1 и наконец подставляем в (4): Fmax× cosa = (m1 + m2) × аmax откуда: Fmax× cosa = (m1 + m2) × m× (m2g – Fmax× sina)/m1
окончательно находим: Ответ на вопрос об ускорении тележки состоит из двух частей: если сила трения не достигла своего предельного значения, то ускорение тележки находится из равенства для системы «груз-тележка», т.е. а1=Fcosa/(m1+m2), иначе а1=аmax и не меняется при дальнейшем увеличении силы F. Получаем:
Вычисления предлагается сделать читателю. ¨
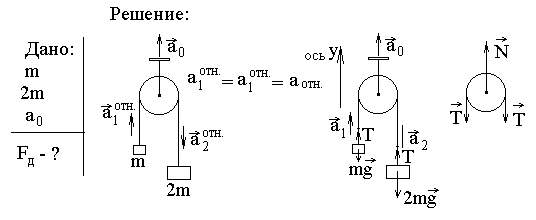
Задача-пример 2. Через невесомый блок перекинута веревка с грузами m и 2m. Блок движется вверх с ускорением а0. Пренебрегая трением, найти давление блока на ось.
Будем искать решение задачи, отталкиваясь от того, что требуется найти. По условию задачи требуется определить силу FД, с которой блок действует на ось, поднимающую его вверх с силой N. По 3-му закону Ньютона: FД = N. Т.е. теперь надо искать величину силы N, приложенной к блоку, а для этого придется записать 2-й закон Ньютона для блока. Методическое указание. Чтобы найти неизвестную силу часто необходимо: 1) определить на какое тело она действует (к какому телу приложена); 2) записать равенство, включающее эту силу, коим является 2-й закон Ньютона для этого тела. Иначе говоря, формула (2.2) – основное равенство, включающее в себя величины действующих на тело сил и позволяющее выразить из нее искомую силу, если только для нее нет иной «личной» формулы-определения, формулы-зависимости (взаимосвязи с другими величинами, данными в задаче, например, формула (2.5) для силы трения) или иной формулы-закономерности (например, формула (2.4) для силы упругости).
На блок действуют три силы: Заметим, что при отсутствии трения между нитью (веревкой) и блоком, а также если нет трения между осью и блоком и масса блока принимается равной нулю (блок невесомый), то величины сил натяжения нитей, приложенных к разным сторонам блока, равны между собой. Поэтому на рисунке мы обозначаем их одинаково. Получаем в проекциях на направление движения: mблокаa0 = N – 2T. Т.к. по условию mблока = 0, то N = 2T. И теперь переходим к нахождению силы T, рассматривая ее как силу, приложенную к грузам. Первый груз массой m движется вверх под действием двух сил mg и T с ускорением а1. Аналогично второй груз массой 2m движется под действием сил 2mg и T с ускорением а2 (на рис. точное направление Здесь необходимо обратить внимание на ответы на следующие вопросы: 1. В каком направлении движется второй груз (вверх или вниз)? 2. Равны ли по модулю ускорения а1 и а2? Почему? 3. Что одинаково при движении грузов, связанных одной нитью? Методическое указание. Важно вспомнить, что все величины, участвующие в записи 2-го закона Ньютона должны быть заданы в одной и той же ИСО. Тогда замечаем, что система отсчета, связанная с блоком, который движется с ускорением относительно Земли, не является инерциальной (по определению). Значит, ускорения грузов должны быть определены относительно неподвижной системы отсчета, той, относительно которой рассматривается движение самого блока! Что же касается движения грузов относительно блока, то оно равноускоренное и соответствующее ускорение, одинаковое для обоих грузов, обозначим через аотн. Тогда абсолютные ускорения грузов нужно будет находит по формуле, аналогичной формуле сложения скоростей (см. раздел Кинематика, Относительность движения): Итак, записываем 2-й закон Ньютона для каждого груза в проекциях на ось у: ma1у = T– mg и 2mа2у = Т – 2mg (а). С учетом формулы (2.6) имеем: Тогда в проекциях на ту же ось: а1у=а0 + аотн и а2у = а0 – аотн. Теперь видно, что т.к. ускорение первого груза, равное сумме двух положительных величин, положительно, то он движется вверх. А вот про второй груз ничего однозначно утверждать нельзя, т.к. знак полного ускорения его зависит от соотношения величин а0 и аотн: если а0 > аотн, то второй груз будет двигаться вверх (по направлению оси у), если а0 < аотн, то – вниз (противоположно оси у). Подставляем в (а): Т – mg = m(а0 + аотн) и Т – 2mg = 2m(а0 – аотн). Таким образом получаем два уравнения с двумя неизвестными Т и аотн, откуда, исключая вторую неизвестную, находим значение силы натяжения нити, затем силу N и дает окончательный ответ на вопрос задачи. Умножаем первое уравнение на 2 и почленно складываем со вторым: 2(T - mg) + (Т – 2mg) = 2m(а0 + аотн) + 2m(а0 – аотн), раскрываем скобки и приводим подобные слагаемые: 3Т – 4 mg = 4mа0, отсюда 3Т = 4m(а0 +g) или Т = 4/3m(а0 +g). Тогда сила давления блока на ось равна Fд = 8/3m(а0 +g). ¨ Методическое указание. В задачах с участием блоков возможны следующие случаи: 1) установка включает подвижный блок; 2) блок в конструкции закреплен неподвижно, относительно своей оси; 3) подвижный и неподвижный блок соединены общей, одной нитью. В первом и во втором случаях чаще всего оказываются равными силы натяжения нити в различных ее участках, а сам блок необходим только для изменения направления действия силы (например, в случае поднятия груза с помощью нити перекинутой через неподвижный блок: с какой силой тянем веревку, такая и поднимает груз). В третьем случае, система из одной пары «подвижного и неподвижного» блоков позволяет кроме того получать выигрыш в силе в два раза.
Задача-пример 3. К оси подвижного блока прикреплен груз массой m. С какой силой F нужно тянуть конец нити, перекинутой через второй блок, чтобы груз двигался вверх с ускорением а? Чтобы груз покоился? Массой блоков и нити пренебречь.
T = F (б) Рассматривая 2-й закон Ньютона для подвижного блока, получим Р = 2Т (в), т.к. масса блока равна нулю. По 3-му закону Ньютона Р = N (г), т.е. сила с которой груз действует на ось блока, равна силе, с которой ось действует на груз. Из 2-го закона Ньютона для груза в проекциях на направление движения имеем: ma = N – mg, подставим (б), (в) и (г): ma = 2F – mg, откуда F = ½ m(a + g). ¨ Замечания. Отметим, что неподвижный блок применяется только для изменения направления действия силы. Тогда как подвижный блок в случае, если нити с обеих сторон параллельны (расстояние между точками их касания о блок равно 2R) дает выигрыш в силе в 2 раза (рассматривается поворот блока относительно одной из точек касания его с нитью). Последовательное соединение нескольких пар чередующихся подвижного и неподвижного блоков дает конструкцию с выигрышем в силе в несколько раз.
Большую группу задач образуют задачи, рассматривающие движение тел по наклонной плоскости. Выделим несколько основных моментов, на которые следует обращать внимание при их решении. Методические указания. Возможны два случая: 1) наклонная плоскость неподвижна относительно горизонтальной поверхности. В этом случае ускорение тела относительно наклонной плоскости является его абсолютным ускорением и может быть включено в запись закона Ньютона для тела. Также необходимо определить вид движения (т.е. есть ли ускорение или же оно равно нулю). Ускорение тела равно нулю, если оно покоится или движется с постоянной скоростью. Второй закон Ньютона лучше записывать в форме 3 для равнодействующей силы (общий случай). А направление осей чаще всего должны выбираться вдоль наклонной плоскости (ось х) и перпендикулярно к ней (ось у). Проецирование на эти оси приводит к получению двух скалярных равенств для сил, действующих на тело. Кроме них, при наличии трения о наклонную плоскость при скольжении тела записывается и будет обязательно использоваться при решении задачи формула (2.5) для силы трения скольжения. Она же включается в решение при условии, что тело не скользит, но находится в граничном состоянии (т.е. вот-вот начнет скользить или только что скользить перестало). Дополнением могут быть некоторые кинематические зависимости. 2) наклонная плоскость сама движется с ускорением. Тогда 2-й закон Ньютона нельзя записывать относительно наклонной плоскости, т.е. ускорение тела должно быть определено относительно неподвижной системы отсчета (по формуле (2.6)), в которой и будет записываться формула (2.2), как для тела, так и для плоскости, если это необходимо и требуется исходя из условия и данных задачи.
Задача-пример 4. С каким ускорением должна двигаться наклонная плоскость в горизонтальном направлении, чтобы находящееся на ней тело массой m не двигалось относительно наклонной плоскости при условии отсутствия трения?
х: mgsina + 0 = ma, отсюда и находим: а = gsina, ¨ y: -mgcosa + N = 0. Методические указания. Проектировать векторное равенство необходимо почленно: переходя от первого слагаемого ко второму и т.д. и внимательно определяя проекции каждого из них. Для этого учитываем правила: если вектор направлен вдоль оси, то величина его проекции равна модулю соответствующей силы, а знак определяется по совпадению или несовпадению направлений оси и вектора этой силы («+» и «-» соответственно). Если же вектор силы направлен под углом к оси, то проводим через его начало прямую, параллельную оси, опускаем из конца вектора на эту прямую перпендикуляр и получаем прямоугольный треугольник, один из острых углов которого равен углу наклона плоскости a (находим его по правилу: углы, образованные взаимно перпендикулярными сторонами равны). Тогда из соотношений длин и величин углов в прямоугольном треугольнике находим длину катета, равного величине проекции силы на ось, и аналогично определяем знак этой проекции.
Здесь можно привести и другой подход. Известно, что любой вектор можно разложить на две взаимно перпендикулярные составляющие различными способами. Тогда проекция вектора на ось совпадает с проекцией соответствующей составляющей его на эту ось.
ЗАДАЧИ к разделу «Динамика»
|


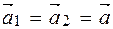 ; 2) тела движутся по-разному, т.е. груз скользит по тележке и его ускорение больше по величине, т.е. а1 < а2. Но в обоих случаях тела движутся с ускорениями. Ответим на вопрос о том, какая сила сообщает каждому из рассматриваемых тел это ускорение.
; 2) тела движутся по-разному, т.е. груз скользит по тележке и его ускорение больше по величине, т.е. а1 < а2. Но в обоих случаях тела движутся с ускорениями. Ответим на вопрос о том, какая сила сообщает каждому из рассматриваемых тел это ускорение. под действием двух сил (приложенной к нему внешней силы
под действием двух сил (приложенной к нему внешней силы 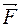 исилы трения
исилы трения  ). Второй закон Ньютона для него запишется в форме 2 (см. методические указания на с.46) для проекций сил:
). Второй закон Ньютона для него запишется в форме 2 (см. методические указания на с.46) для проекций сил: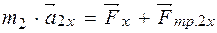 ,
, или
или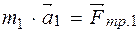 ,
, !
! Методическое указание. Сложным моментом является понимание диалектики предельных значений. Так, максимальное значение силы F, когда груз все еще не движется по тележке, есть то же самое, что и минимальное значение силы F, когда груз еще движется по тележке. Разница состоит в направлении подхода к данному граничному значению силы. Иначе говоря, значение Fmax разбивает всю совокупность возможных значений силы F на два множества: 1) значения, при которых груз не скользит по тележке; 2) значения, при которых груз скользит по тележке. Эти множества не пересекаются (не имеют общих элементов). Каждый элемент первого из них меньше всякого элемента из второго множества (чтобы заставить груз скользит надо очевидно увеличить приложенную силу!). Само же значение Fmax находится и в одном и в другом, т.к. является их общей границей. Но когда идет речь о границе первого множества, то граница именуется как Fmax, граница второго множества по отношению к остальным его элементам является минимальной величиной и обозначается Fmin. Значения Fmin и Fmax равны. Но когда мы ищем Fmin мы находимся к условиях скольжения груза, если же ищем предельное значение в виде Fmax, то считаем, что груз не скользит по тележке, а значит они движутся как одно целое с равными по величине ускорениями.
Методическое указание. Сложным моментом является понимание диалектики предельных значений. Так, максимальное значение силы F, когда груз все еще не движется по тележке, есть то же самое, что и минимальное значение силы F, когда груз еще движется по тележке. Разница состоит в направлении подхода к данному граничному значению силы. Иначе говоря, значение Fmax разбивает всю совокупность возможных значений силы F на два множества: 1) значения, при которых груз не скользит по тележке; 2) значения, при которых груз скользит по тележке. Эти множества не пересекаются (не имеют общих элементов). Каждый элемент первого из них меньше всякого элемента из второго множества (чтобы заставить груз скользит надо очевидно увеличить приложенную силу!). Само же значение Fmax находится и в одном и в другом, т.к. является их общей границей. Но когда идет речь о границе первого множества, то граница именуется как Fmax, граница второго множества по отношению к остальным его элементам является минимальной величиной и обозначается Fmin. Значения Fmin и Fmax равны. Но когда мы ищем Fmin мы находимся к условиях скольжения груза, если же ищем предельное значение в виде Fmax, то считаем, что груз не скользит по тележке, а значит они движутся как одно целое с равными по величине ускорениями.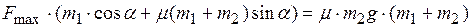
 .
. при
при 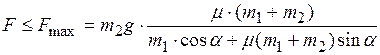 и
и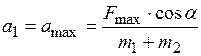 при
при  .
.
 ,
,  и
и 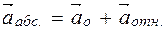 (2.6).
(2.6). – для первого груза и
– для первого груза и  – для второго груза, где аотн1= аотн2.
– для второго груза, где аотн1= аотн2.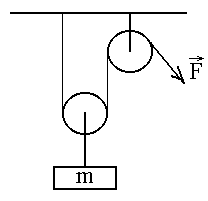
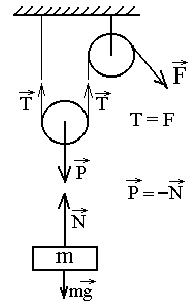 Решение. Прежде всего, заметим, что сила натяжения нити в любой ее точке одинакова и равна по величине силе, с которой тянут за конец нити:
Решение. Прежде всего, заметим, что сила натяжения нити в любой ее точке одинакова и равна по величине силе, с которой тянут за конец нити: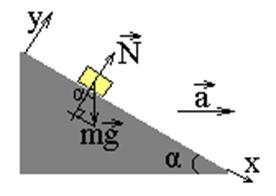 Решение: Прежде всего, заметим, что система отсчета, связанная с наклонной плоскостью не является инерциальной. Поэтому нельзя рассматривать движение тела относительно нее с целью записать второй закон Ньютона. А значит будем рассматривать движение тела относительно горизонтальной неподвижной плоскости С1. В С1 наклонная плоскость движется с ускорением
Решение: Прежде всего, заметим, что система отсчета, связанная с наклонной плоскостью не является инерциальной. Поэтому нельзя рассматривать движение тела относительно нее с целью записать второй закон Ньютона. А значит будем рассматривать движение тела относительно горизонтальной неподвижной плоскости С1. В С1 наклонная плоскость движется с ускорением  , и если тело не движется по наклонной плоскости, то это значит, что оно движется точно также как и сама наклонная плоскость, т.е. с тем же ускорением
, и если тело не движется по наклонной плоскости, то это значит, что оно движется точно также как и сама наклонная плоскость, т.е. с тем же ускорением  - векторная форма. В проекциях на оси
- векторная форма. В проекциях на оси



