Примеры решения задач. Задача-пример 1. Тело массой 20 г движется со скоростью 10 м/с под углом 600 к вертикальной стенке
Далее, записываем формулу изменения импульса: Вычисляем: Ответ: 0, 2 кг× м/с в перпендикулярном к стенке направлении от нее. ¨ Методические указания. Прежде всего заметим, что изменение векторной величины – тоже вектор. А поэтому ответ на вопрос задачи состоит из числового значения и описания его направления. Далее примечательно проанализировать полученный ответ. В частности, как можно без построения «треугольника импульсов» определить направление вектора изменения импульса тела? Чтобы ответить, необходимо обратиться к формуле (4.17): вектора, стоящие справа и слева от знака равенства одинаково направлены, т.е. изменение импульса всегда имеет такое же направление, как и сила, его вызывающая. В данном примере изменение импульса происходит под действием силы реакции опоры (стенки), которая, как известно, всегда перпендикулярна опоре и направлена от нее. Полученному в задаче значению равен и импульс силы реакции стенки, в соответствии с законом (4.17). Т.е. чтобы найти импульс силы, вовсе не обязательно знать ее значение и время ее действия. К тому же сила в течение промежутка времени своего действия на тело может быть далеко не постоянной по модулю величиной: в начале большей, а в конце меньшей!
Задача-пример 2. Конькобежец, стоя на коньках на льду, бросает груз массой 10 кг под углом 300 к горизонту со скоростью 5 м/с. Какова будет начальная скорость движения конькобежца, если его масса равна 64 кг? Перемещение конькобежца во время броска пренебречь.
Ответ: 0, 68 м/с в сторону от груза по горизонтали ¨ Методические указания. Возможны два варианта решения: 1) когда мы сразу можем точно установить (и обосновать выбор) истинное направление скорости после ее изменения, тогда изображаем ее на рисунке и в равенство входит модуль этой скорости, откуда его и находим; 2) истинное направление движения после события неизвестно, тогда на рисунке скорость не указывается или рисуется произвольно, а в равенство входит ее проекция на ось. Далее по найденному значению проекции, с учетом ее знака, дается ответ о значении и направлении искомой скорости. Решенная выше задача демонстрирует второй вариант.
Задача-пример 3. На какое расстояние сместится неподвижно стоящая на воде лодка, если человек массой m 1 = 70 кг пройдет с носа лодки на корму? Длина лодки 2, 5 м, ее масса m 2 = 100 кг. Сопротивлением воды пренебречь.
Относительно центра лодки (точки О) радиус вектор точки С меняет лишь направление: на противоположное (с «вправо» на «влево»), оставаясь (с учетом симметрии лодки и положения человека на ней до и после перехода) одинаковым по величине и равным в соответствии с формулой (4.19): Вычислим:
Задача-пример 4. На гладкой горизонтальной плоскости находится тело массы М (рис.) и на нем небольшая шайба массы m. Последней сообщили в горизонтальном направлении скорость v. На какую высоту (по сравнению с первоначальным уровнем) поднимется шайба после отрыва от тела М? Трения нет.
Учтем, что шайба, не отрываясь от тела М (и после отрыва), продолжает движение вдоль оси х со скоростью
Получили систему из двух уравнений (I)-(II) с двумя неизвестными
Ответ:
Рассмотрим переход системы из второго состояния в третье (рис. б и в). При этом выполняется закон сохранения полной механической энергии: Е2 = Е3
Ответ:
Задача-пример 6. От груза, висящего на пружине жесткости k, отрывается часть массой m. На какую высоту поднимется после этого оставшаяся часть груза.
2) рассмотрим два состояния груза без массы m: сразу после отрыва и на искомой высоте, где он НЕ находится в равновесии. При переходе системы (груз на пружине) из первого состояния во второе выполняется закон сохранения полной механической энергии (т.к. действуют лишь потенциальные силы):
Считая, что, поднявшись на искомую высоту, груз все еще растягивает пружину (т.е.
Þ
В этой связи очень важно для четкости аргументации пояснять о чем идет речь: о каком-либо одном состоянии тела или системы, рассматриваемой в задаче, или о процессе перехода из первого состояния во второе, минуя множество состояний промежуточных. Так вот для того, чтобы выполнялись законы сохранения полной механической энергии или импульса (приравнивающие механические характеристики концевых точек интервала) необходимо выявить и уяснить выполнение какого-либо из условий (,) непременно для каждого переходного состояния. Тот факт, что указанные условия справедливы в конечных состояниях никак не доказывает того, что переход осуществлен без их нарушения!!! Таким образом, решение задач на законы сохранения сводится к: 1) выбору состояний, 2) записи выражений для энергии и импульса системы в этих состояниях и 3) приравниванию полученных выражений на основе обоснования выполнения соответствующего величине закона сохранения.
ЗАДАЧИ к разделу «Энергия»
|

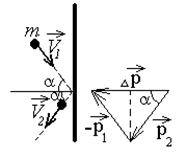 Задача-пример 1. Тело массой 20 г движется со скоростью 10 м/с под углом 600 к вертикальной стенке. Определить изменение импульса тела в результате абсолютно упругого столкновения его со стенкой.
Задача-пример 1. Тело массой 20 г движется со скоростью 10 м/с под углом 600 к вертикальной стенке. Определить изменение импульса тела в результате абсолютно упругого столкновения его со стенкой.

 Решение: Делаем рисунок: указываем направление скорости тела до и после удара о стенку. Напраление импульса совпадает с направлением соответствующей скорости. Т.к. удар о стенку считается абсолютно упругим, то величина скорости (а значит и импульса) не меняется. Изменением направления скорости показано на рисунке.
Решение: Делаем рисунок: указываем направление скорости тела до и после удара о стенку. Напраление импульса совпадает с направлением соответствующей скорости. Т.к. удар о стенку считается абсолютно упругим, то величина скорости (а значит и импульса) не меняется. Изменением направления скорости показано на рисунке. и на ее основе строим «треугольник импульсов», из которого геометрически находим длину нужной стороны, равную искомой физической величине: т.к.
и на ее основе строим «треугольник импульсов», из которого геометрически находим длину нужной стороны, равную искомой физической величине: т.к. 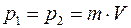 , то
, то  - модуль изменения импульса. А направлен вектор
- модуль изменения импульса. А направлен вектор 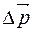 перпендикулярно стенке от нее.
перпендикулярно стенке от нее. (кг× м/с).
(кг× м/с).
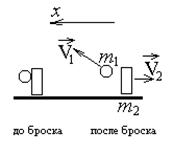 Решение: На рисунке указываем векторы импульсов тел до и после изменения их движения и положительное направление координатной оси (по горизонтали
Решение: На рисунке указываем векторы импульсов тел до и после изменения их движения и положительное направление координатной оси (по горизонтали  в сторону полета груза). В интересующем нас горизонтальном направлении на систему тел «конькобежец – груз» внешние силы не действуют, поэтому можно воспользоваться формулой
в сторону полета груза). В интересующем нас горизонтальном направлении на систему тел «конькобежец – груз» внешние силы не действуют, поэтому можно воспользоваться формулой  (4.18*):
(4.18*):  , где
, где  - проекция импульса данной системы до броска, а
- проекция импульса данной системы до броска, а  - после броска. Учитывая, что проекция импульса системы равна сумме проекций импульсов ее частей и до броска оба тела покоились (суммарный импульс системы равен нулю), получаем скалярное равенство:
- после броска. Учитывая, что проекция импульса системы равна сумме проекций импульсов ее частей и до броска оба тела покоились (суммарный импульс системы равен нулю), получаем скалярное равенство: 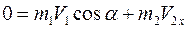 , отсюда выражаем:
, отсюда выражаем: 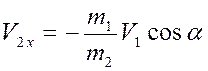 . Вычисляем:
. Вычисляем:  (м/с). Знак «–» означает (исходя из определения проекции вектора на ось), что скорость конькобежца после броска направлена противоположно выбранному положительному направлению оси, т.е. груз и человек будут двигаться по горизонтали в противоположных направлениях.
(м/с). Знак «–» означает (исходя из определения проекции вектора на ось), что скорость конькобежца после броска направлена противоположно выбранному положительному направлению оси, т.е. груз и человек будут двигаться по горизонтали в противоположных направлениях.


 Решение: В данной задаче имеем дело уже не с одним телом, а с системой двух тел «лодка-человек». Т.к. в направлении оси х на систему не действуют внешние силы, то при переходе системы из состояния 1 в состояние 2 ее импульс не меняется, т.е. остается равен нулю. Тогда получаем, что скорость центра масс системы тоже остается равна нулю в течение всего перехода, т.е. точка С (рис.) неподвижна в процессе перехода человека с носа лодки на корму.
Решение: В данной задаче имеем дело уже не с одним телом, а с системой двух тел «лодка-человек». Т.к. в направлении оси х на систему не действуют внешние силы, то при переходе системы из состояния 1 в состояние 2 ее импульс не меняется, т.е. остается равен нулю. Тогда получаем, что скорость центра масс системы тоже остается равна нулю в течение всего перехода, т.е. точка С (рис.) неподвижна в процессе перехода человека с носа лодки на корму.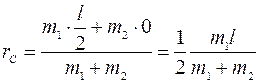 . Из рисунка видно, что лодка при этом должна сместиться на расстояние
. Из рисунка видно, что лодка при этом должна сместиться на расстояние  .
. (м). Ответ: 1 м ¨
(м). Ответ: 1 м ¨

 Решение: Когда шайба m начинает менять направление движения, двигаясь по изгибу тела М, то тело М вследствие отсутствия силы трения начинает двигаться тоже. Считая, что время такого взаимодействия мало, можно воспользоваться законом сохранения проекции импульса системы «M-m» на горизонтальную ось х:
Решение: Когда шайба m начинает менять направление движения, двигаясь по изгибу тела М, то тело М вследствие отсутствия силы трения начинает двигаться тоже. Считая, что время такого взаимодействия мало, можно воспользоваться законом сохранения проекции импульса системы «M-m» на горизонтальную ось х: (I).
(I). , не меняя ее вследствие отсутствия горизонтальных сил. Также т.к. в системе «M-m» отсутствуют диссипативные силы (сила трения), а внешние силы (тяжести) потенциальны (внешнего трения тоже нет), то для нее выполняется закон сохранения полной механической энергии:
, не меняя ее вследствие отсутствия горизонтальных сил. Также т.к. в системе «M-m» отсутствуют диссипативные силы (сила трения), а внешние силы (тяжести) потенциальны (внешнего трения тоже нет), то для нее выполняется закон сохранения полной механической энергии: (II).
(II). , тогда
, тогда 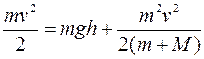 Þ
Þ  и, наконец,
и, наконец,  .
. Задача-пример 5. С какой силой нужно надавить на верхний груз массы m1, чтобы нижний груз массы m2, соединенный с верхним пружиной, оторвался от пола после прекращения действия этой силы?
Задача-пример 5. С какой силой нужно надавить на верхний груз массы m1, чтобы нижний груз массы m2, соединенный с верхним пружиной, оторвался от пола после прекращения действия этой силы?

 Решение: Рассмотрим три состояния системы, состоящей из двух грузов, соединенных пружиной. В исходном состоянии (рис.а) пружина сжата на D х и верхний груз находится в равновесии, поэтому:
Решение: Рассмотрим три состояния системы, состоящей из двух грузов, соединенных пружиной. В исходном состоянии (рис.а) пружина сжата на D х и верхний груз находится в равновесии, поэтому: 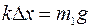 . Далее под действием силы
. Далее под действием силы 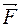 пружина сжимается еще на величину х, верхний груз также уравновешен:
пружина сжимается еще на величину х, верхний груз также уравновешен:  . В конечном состоянии пружина растянута на величину h и нижний груз не давит на опору:
. В конечном состоянии пружина растянута на величину h и нижний груз не давит на опору: 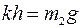 . Из полученных трех равенств получаем:
. Из полученных трех равенств получаем: -?. Т.е. теперь ищем величину
-?. Т.е. теперь ищем величину  .
. ,
, ½ × k
½ × k
 ¨
¨
 Решение: 1) До отрыва массы m условие равновесия имеет вид:
Решение: 1) До отрыва массы m условие равновесия имеет вид: kx1=(M+m)g (I), где M+m – масса груза, x1 - относительное удлинение пружины.
kx1=(M+m)g (I), где M+m – масса груза, x1 - относительное удлинение пружины.
 ½ × 2
½ × 2
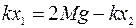 (II).
(II).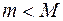 ), т.е. и х1 и х2 – деформации растяжения, получим в качестве искомого расстояния величину (х1 - х2). Имеем:
), т.е. и х1 и х2 – деформации растяжения, получим в качестве искомого расстояния величину (х1 - х2). Имеем:
 . ¨
. ¨
 Методические указания и рекомендации. Проводя сравнение используемых в механике физических величин, можно сделать вывод, что одни из них (путь, промежуток времени, перемещение, средняя скорость, ускорение, работа, изменение энергии или импульса и др.) есть величины интервальные (соответствующие какому-либо интервалу и характеризующие процесс, участок и пр.), а другие (мгновенные скорость и ускорение, энергия, импульс, момент времени и пр.) - точечные (относящиеся к точке пространства, временной точке, одному определенному состоянию и т.д.).
Методические указания и рекомендации. Проводя сравнение используемых в механике физических величин, можно сделать вывод, что одни из них (путь, промежуток времени, перемещение, средняя скорость, ускорение, работа, изменение энергии или импульса и др.) есть величины интервальные (соответствующие какому-либо интервалу и характеризующие процесс, участок и пр.), а другие (мгновенные скорость и ускорение, энергия, импульс, момент времени и пр.) - точечные (относящиеся к точке пространства, временной точке, одному определенному состоянию и т.д.).


