 Рассмотрим кручение при деформации цилиндрической пружины.
Рассмотрим кручение при деформации цилиндрической пружины.  На рис.7.3 цилиндрическая пружина диаметром
На рис.7.3 цилиндрическая пружина диаметром  и длиной
и длиной  , подверженная растяжению до длины
, подверженная растяжению до длины  двумя равными и противоположно направленными вдоль ее оси силами
двумя равными и противоположно направленными вдоль ее оси силами  . Будем рассматривать пружину, как винтовую линию с пренебрежимо малым шагом, таким, что каждый ее виток перпендикулярен силам, действующим на пружину. Момент сил, действующий в любом сечении витка пружины в таком случае является постоянной величиной, равной
. Будем рассматривать пружину, как винтовую линию с пренебрежимо малым шагом, таким, что каждый ее виток перпендикулярен силам, действующим на пружину. Момент сил, действующий в любом сечении витка пружины в таком случае является постоянной величиной, равной  , где
, где  - радиус пружины. Вектор момента сил направлен по касательной к витку, и следовательно, вызывает деформацию чистого кручения витков пружины. Следствием этой деформации будет изменение длины пружины, т.е. ее линейная деформация.
- радиус пружины. Вектор момента сил направлен по касательной к витку, и следовательно, вызывает деформацию чистого кручения витков пружины. Следствием этой деформации будет изменение длины пружины, т.е. ее линейная деформация.
Для экспериментального определения жесткости пружины используют пружинный маятник. В данной работе изучаются свободные колебания груза известной массы  , подвешенного на пружине. Зависимость отклонения равновесного положения груза от времени
, подвешенного на пружине. Зависимость отклонения равновесного положения груза от времени  подчиняется следующему уравнению динамики:
подчиняется следующему уравнению динамики:  . Решение этого уравнения имеет вид:
. Решение этого уравнения имеет вид:  , где амплитуда
, где амплитуда 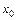 и начальная фаза
и начальная фаза  определяются начальными условиями;
определяются начальными условиями;  – угловая частота колебаний, период которых Т равен:
– угловая частота колебаний, период которых Т равен: 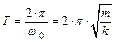 , где
, где  – жесткость пружины. Зная
– жесткость пружины. Зная  , можно определить модуль сдвига:
, можно определить модуль сдвига:
 , (7.7)
, (7.7)
где  – диаметр пружины,
– диаметр пружины, 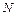 – число витков пружины,
– число витков пружины,  – масса подвешенного груза,
– масса подвешенного груза,  – диаметр проволоки.
– диаметр проволоки.
При определении модуля сдвига материалов методом растяжения пружины, необходимо подвешивать к пружине грузы разной массы  и
и 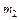 , измеряя соответствующие удлинения
, измеряя соответствующие удлинения  и
и  . Модуль сдвига в этом случае будет определяться как:
. Модуль сдвига в этом случае будет определяться как:
 , (7.8)
, (7.8)
где  – радиус пружины,
– радиус пружины, 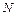 – число витков пружины,
– число витков пружины,  – удлинение пружины,
– удлинение пружины,  – диаметр проволоки.
– диаметр проволоки.

 Рассмотрим кручение при деформации цилиндрической пружины.
Рассмотрим кручение при деформации цилиндрической пружины.  На рис.7.3 цилиндрическая пружина диаметром
На рис.7.3 цилиндрическая пружина диаметром  и длиной
и длиной  , подверженная растяжению до длины
, подверженная растяжению до длины  двумя равными и противоположно направленными вдоль ее оси силами
двумя равными и противоположно направленными вдоль ее оси силами  . Будем рассматривать пружину, как винтовую линию с пренебрежимо малым шагом, таким, что каждый ее виток перпендикулярен силам, действующим на пружину. Момент сил, действующий в любом сечении витка пружины в таком случае является постоянной величиной, равной
. Будем рассматривать пружину, как винтовую линию с пренебрежимо малым шагом, таким, что каждый ее виток перпендикулярен силам, действующим на пружину. Момент сил, действующий в любом сечении витка пружины в таком случае является постоянной величиной, равной  , где
, где  - радиус пружины. Вектор момента сил направлен по касательной к витку, и следовательно, вызывает деформацию чистого кручения витков пружины. Следствием этой деформации будет изменение длины пружины, т.е. ее линейная деформация.
- радиус пружины. Вектор момента сил направлен по касательной к витку, и следовательно, вызывает деформацию чистого кручения витков пружины. Следствием этой деформации будет изменение длины пружины, т.е. ее линейная деформация. , подвешенного на пружине. Зависимость отклонения равновесного положения груза от времени
, подвешенного на пружине. Зависимость отклонения равновесного положения груза от времени  подчиняется следующему уравнению динамики:
подчиняется следующему уравнению динамики:  . Решение этого уравнения имеет вид:
. Решение этого уравнения имеет вид:  , где амплитуда
, где амплитуда 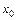 и начальная фаза
и начальная фаза  определяются начальными условиями;
определяются начальными условиями;  – угловая частота колебаний, период которых Т равен:
– угловая частота колебаний, период которых Т равен: 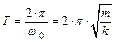 , где
, где  – жесткость пружины. Зная
– жесткость пружины. Зная  , (7.7)
, (7.7)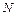 – число витков пружины,
– число витков пружины,  – диаметр проволоки.
– диаметр проволоки. и
и 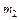 , измеряя соответствующие удлинения
, измеряя соответствующие удлинения  и
и  . Модуль сдвига в этом случае будет определяться как:
. Модуль сдвига в этом случае будет определяться как: , (7.8)
, (7.8) – удлинение пружины,
– удлинение пружины, 


