Дифференциальные уравнения Эйлера равновесия жидкости
В покоящейся однородной жидкости расположим декартовы оси координат произвольным образом. В первом квадранте выделим элементарный объем в виде параллелепипеда с ребрами dx, dy и dz, параллельными соответствующим осям координат (рис. 3.3). Предположим, что жидкость в нем затвердела. Тогда на грани параллелепипеда действуют силы давления dF1…6 от окружающей жидкости, а в его центре масс (точка О) приложена равнодействующая всех массовых сил dG. Для покоящейся жидкости dG является силой тяжести. При таких допущениях условия равновесия не нарушаются. Рассмотрим условия равновесия данного параллелепипеда для оси Х:
Равнодействующая всех массовых сил dG равна:
dG=ρ dx dy dz j,
где j – ускорение, вызванное силой dG. Тогда проекция dG на ось Х будет иметь вид:
dGх=ρ dx dy dz jх.
Подставим соответствующие значения проекций сил в уравнение (3.7) и разделим на ρ dx dy dz. В результате получим:
Проведя аналогичные рассуждения для осей Y и Z получим дифференциальные уравнения равновесия жидкости Эйлера:
Для удобства практического использования вместо системы уравнений (3.8) получим одно эквивалентное уравнение. Для этого умножим первое уравнение системы (3.8) на dx, втрое – на dy, третье – на dz и сложим эти уравнения. В результате получим:
Трехчлен, находящийся в скобках, является полным дифференциалом давления dp (см. 3.3). С учетом этого уравнение (3.9) примет вид:
Уравнение (3.10) получено Эйлером в 1755 г. называют дифференциальным уравнением равновесия жидкости или основным уравнением гидростатики в дифференциальной форме. Уравнение (3.10) справедливо также и для газа при совместном использовании с уравнением Клапейрона – Менделеева (2.12).
|

 . (3.7)
. (3.7) Обозначим давление в центре масс параллелепипеда через р. Тогда в соответствии с уравнением (3.3) давление в точке приложения силы dF1 (точка А) будет равно
Обозначим давление в центре масс параллелепипеда через р. Тогда в соответствии с уравнением (3.3) давление в точке приложения силы dF1 (точка А) будет равно  . Соответственно, давление в точке приложения силы dF2 (точка В) давление будет равно
. Соответственно, давление в точке приложения силы dF2 (точка В) давление будет равно  . Так как площадь грани, на которую действует сила dF1, бесконечно мала, то давление в точках А и В можно считать средним гидростатическим давлением, действующим на соответствующие грани. Тогда:
. Так как площадь грани, на которую действует сила dF1, бесконечно мала, то давление в точках А и В можно считать средним гидростатическим давлением, действующим на соответствующие грани. Тогда: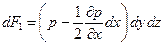 , а
, а  .
.

 (3.8)
(3.8) (3.9)
(3.9) (3.10)
(3.10)


