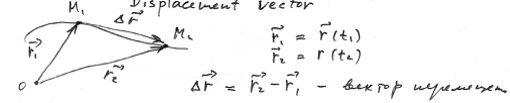Средние и мгновенные скорость и ускорение
Вращательное движение. Вектор элементарного углового перемещения. Векторы угловой скорости и углового ускорения. Векторная связь линейной и угловой скорости. Степени свободы твердого тела. Описание поступательного движения т.т. и вращения вокруг неподвижной оси. Плоское движение т.т. Мгновенная ось вращения. Материальная точка (м.т.) – модель физического тела, размерами, формой и внутренней структурой которого можно пренебречь в условиях данной задачи. Существует 3 способа описания движения точки: вектор., координат., естеств. Векторный способ. В этом случае положение материальной точки задается с помощью радиус вектора r, представляющий собой вектор, проведенный из точки О, соответствующей началу отсчета, в интересующую нас точку А. В процессе движения материальной точки её радиус-вектор может меняться по модулю и направлению траектории точки. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать ее радиус-вектор Геометрическое место концов радиуса-вектора r называют траекторией точки А.
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной. Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Координатный способ задания движения точки. В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения: x =x(t) y=y(t) (1.4) z=z(t)
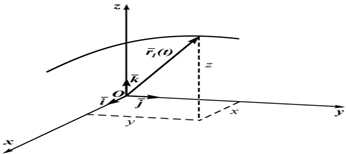
Рисунок 1.3
Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей. Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3): _ _ _ _ r(t)=ix(t) + jy(t) + kz(t) (1.5) \k\=\i\=\j\ =1 – орты
|
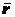как функцию времени: 
