Связь силы с потенциальной энергией
Если известно выражение потенциальной энергии Wp(x, y, z), то можно найти силу, действующую на тело в любой точке силового поля. Пусть тело (частица) или м.т. перемещается в пространстве. При этом силы поля совершают над частицей элементарную работу
Следовательно, A = Fx dx + Fy dy + Fz dz, Ах = Fxdx, Аy = Fydy, Аz = Fzdz. С другой стороны A = dWp . Поскольку потенциальная энергия является полным дифференциалом, то Анализируя рассмотренное выше, получаем, что
Таким образом,
∆ (перевернутый)оператор Гамильтона в декартовых координатах. (Знак “∆ “ - называют оператором набла). Таким образом, Выражение " gradWp" или (dWp/dn) называют градиентом потенциальной энергии по направлению dn (наибольшая быстрота изменения потенциальной энергии по данному направлению). Знак “ “ показывает, что вектор силы, действующий на частицу, направлен в сторону убывания потенциальной энергии. Потенциальная яма – область пространства, где потенциальная энергия частицы меньше чем в окружающем пространстве. Потенциальная яма обычно отвечает короткодействующим силам притяжения. В области действия этих сил потенциал отрицателен, вне – нулевой.
Потенциальный барьер – область пространства, где потенциальная энергия частицы больше чем в окружающем пространстве. Положение равновесия – состояние тела, при котором равнодействующая всех сил равна нулю и сумма моментов этих сил относительно любой точки также равна нулю. Устойчивое равновесие – состояние тела, когда любое смещение тела из состояния равновесия приводит к возникновению силы, возвращающей тело в положение равновесия. Неустойчивое равновесие – состояние тела, когда смещение тела из состояния равновесия приводит к возникновению силы, уводящей тело от положения равновесия. Безразличное равновесие - состояние тела, когда любое смещение тела из состояния равновесия не приводит к возникновению каких-либо сил.
Система уравнений движения т.т. Динамика поступательного движения т.т. Вращение т.т. вокруг неподвижной оси. Момент инерции относительно оси. Основное уравнение динамики вращательного движения. СИСТЕМА УРАВНЕНИЙ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА Поскольку твердое тело обладает в общем случае шестью степенями свободы, то общая система уравнений движения должна содержать шесть независимых уравнений. Их можно представить в виде, определяющем производные по времени от двух векторов: импульса и момента тела. Первое из этих уравнений получается просто путем суммирования уравнений P = и полную действующую на него силу
Хотя мы определили F как сумму всех сил f, действующих на каждую их частиц, в том числе со стороны других частиц тела, фактически в F входят лишь силы, действующие со стороны внешних источников. Все силы взаимодействия между частицами самого тела взаимно сокращаются; действительно, при отсутствии внешних сил импульс тела, как и всякой замкнутой системы, должен сохраняться, т.е. должно быть F =0. Если U — потенциальная энергия твердого тела во внешнем поле, то сила F может быть определена путем дифференцирования ее по координатам центра инерции тела: F = − Действительно, при поступательном перемещении тела на δ R настолько же меняются и радиус-векторы δ U = Отметим в этой связи, что уравнение (34.1) может быть получено и как уравнение Лагранжа по отношению к координатам центра инерции
с функцией Лагранжа (32.4), для которой
Перейдем к выводу второго уравнения движения, определяющего производную по времени от момента импульса M. Для упрощения вывода удобно выбрать «неподвижную» (инерциальную) систему отсчета таким образом, чтобы в данный момент времени центр инерции тела покоился относительно нее. Имеем
В силу сделанного нами выбора системы отсчета (в котором V =0) значение
где K = Поскольку момент М определен относительно центра инерции, он не меняется при переходе от одной инерциальной системы отсчета к другой. Это видно из формулы с R =0. Отсюда следует, что сравнение движения (34.3), полученное здесь при определенном выборе системы отсчета, тем самым, в силу галилеевского принципа относительности, справедливо в любой инерциальной системе. Вектор [ rf ] называется моментом силы f, так что K есть сумма моментов всех сил, действующих на тело. Как и в полной силе F, в сумме (34.4) фактически должны учитываться лишь внешние силы; в соответствии с законом сохранения момента импульса сумма моментов всех сил, действующих внутри замкнутой системы, должна обращаться в нуль. Момент силы, как и момент импульса, зависит, вообще говоря, от выбора начала координат, относительно которого он определен. В (34.3), (34.4) моменты определяются относительно центра инерции тела. При переносе начала координат на расстояние а новые радиус-векторы r ' точек тела связаны со старыми r через r = r '+ a. Поэтому K = или K = K ' + [ aF ]. (34.5) Отсюда видно, в частности, что величина момента сил не зависит от выбора начала координат, если полная сила F =0 (в таком случае говорят, что к телу приложена пара сил). Уравнения (34.3) можно рассматривать как уравнение Лагранжа
по отношению к «вращательным координатам». Действительно, дифференцируя функцию Лагранжа (32.4) по компонентам вектора Ω;. получим
Изменение же потенциальной энергии U при повороте тела на бесконечно малый угол δ φ равно: δ U = − откуда K = − так что
Предположим, что векторы F и K взаимно перпендикулярны. В этом случае всегда можно найти такой вектор a, чтобы в формуле (34.5) K ' обратилось в нуль, так что будет: K = [ aF ]. (34.7) При этом выбор a неоднозначен: прибавление к нему любого вектора, параллельного F, не изменит равенства (34.7), так что условие K '=0 даст не определенную точку в подвижной системе координат, а лишь определенную прямую линию. Таким образом, при K ┴ F действие всех приложенных к нему сил может быть сведено к одной силе F, действующей вдоль определенной прямой линии. Таков, в частности, случай однородного силового поля, в котором действующая на материальную точку сила имеет вид f = e E, где E — постоянный вектор, характеризующий поле, а величина е характеризует свойства частицы по отношению к данному полю. В этом случае имеем F = E Предполагая, что r 0 = Тогда мы получим следующее простое выражение для полного момента сил: K = [ r 0 F ]. (34.9) Таким образом, при движении твердого тела в однородном поле влияние поля сводится к действию одной силы F, «приложенной» в точке с радиус-вектором (34.8). Положение этой точки всецело определяется свойствами самого тела; в поле тяжести, например, она совпадает с центром инерции тела.
ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЕНИЯ ТВЕРДОГО ТЕЛА Используя уравнения:
можем записать
Таким образом, центр инерции механической системы движется как материальная точка, масса которой равна массе всей системы и на которую действует сила, равная главному вектору внешних сил, приложенных к системе. В общем случае движение твердого тела можно рассматривать как сумму двух движений: поступательного со скоростью, равной скорости центра инерции тела, и вращения вокруг центра инерции. Поэтому последнее уравнение часто называют основным уравнением динамики поступательного движения твердого тела.
ВРАЩЕНИЕ Т.Т. ВОКРУГ НЕПОДВИЖНОЙ ОСИ Вращением вокруг неподвижной оси называется такое движение твердого тела, при котором во все время движения две его точки остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все остальные точки тела движутся в плоскостях, перпендикулярных оси вращения, по окружностям, центры которых лежат на оси вращения. Положение вращающегося твердого тела определяется одним параметром - углом φ между начальным положением АМ0О некоторой плоскости, связанной с телом и проходящей через ось, и ее положением АМО в данный момент времени (рис. 1).
Рисунок 1. Закон вращательного движения:
Проекция вектора угловой скорости на ось и определяется зависимостью:
Угловая скорость ω рад/сек связана с числом оборотов в минуту n зависимостями:
Проекция вектора угловой скорости на ось u определяется зависимостью
Скорость и ускорение точки М вращающегося твердого тела определяются соотношениями (рис. 1):
или в скалярной форме:
Частные случаи: 1) равномерное вращение (ε =0):
2) равнопеременное вращение (ε u=const):
МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ОСИ Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: § mi — масса i -й точки, § ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где: § § § Если тело однородно, то есть его плотность всюду одинакова, то
ОСНОВНОЕ УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ " Произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси (z), вокруг которой происходит вращение: " M=dL/dt=I*(dω /dt)=Iβ, (M, L, ω, β - векторные значения)
|

 или
или .
. , где
, где  частные производные от Wp по х, у, z, соответственно, вычисляемые в предположении, что все другие аргументы, кроме рассматриваемых, являются фиксированными.
частные производные от Wp по х, у, z, соответственно, вычисляемые в предположении, что все другие аргументы, кроме рассматриваемых, являются фиксированными.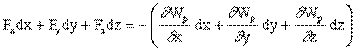 .
. или
или , где выражение
, где выражение
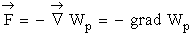


 = f для каждой из составляющих тело частиц, где p — импульс частицы, а f — действующая на нее сила. Вводя полный импульс тела
= f для каждой из составляющих тело частиц, где p — импульс частицы, а f — действующая на нее сила. Вводя полный импульс тела p = μ V
p = μ V = F. (34.1)
= F. (34.1) . (34.2)
. (34.2) каждой точки тела, а потому изменение потенциальной энергии
каждой точки тела, а потому изменение потенциальной энергии δ
δ 
 =
= 
 =
=  p ] +
p ] +  ].
]. . Поскольку же векторы v и p = m v имеют одинаковое направление, то [
. Поскольку же векторы v и p = m v имеют одинаковое направление, то [  = K, (34.3)
= K, (34.3) =
= 
 = Iik Ω k = Mi.
= Iik Ω k = Mi. = −
= −  , (34.6)
, (34.6)
 .
.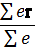 . (34.8)
. (34.8) и
и  ,
, или
или 











 ,
, ,
, — масса малого элемента объёма тела
— масса малого элемента объёма тела  ,
, — плотность,
— плотность, — расстояние от элемента
— расстояние от элемента 



