Векторная связь линейной и угловой скорости
Отдельные точки вращающегося тела имеют различные линейные скорости Линейная скорость точки по определению (2.6) Найдем линейные ускорения точек вращающегося тела. Нормальное ускорение: подставляя значение скорости из (2.6), находим: Тангенциальное ускорение
Воспользовавшись тем же отношением (2.6) получаем (там где епсилант, пишите бета) Таким образом, как нормальное, так и, тангенциальное ускорения растут линейно с расстоянием точки от оси вращения. Степени свободы механической системы – независимые параметры, определяющие положение механической системы в пространстве. Число степеней свободы – в общем случае у м.т. три степени свободы, а у т.т. – шесть степеней свободы: три связаны с поступательным движением и три с вращательным. У сплошной среды число степеней свободы бесконечно велико. Плоское движение т.т. – движение т.т., при котором траектории всех его точек лежат в параллельных плоскостях.
Мгновенная ось вращения – ось, вокруг которой движение твердого тела в данный момент времени можно представить как чистое вращение.
Криволинейное движение. Кривизна траектории. Формулы для тангенциальной и нормальной составляющих вектора полного ускорения. Их характеристика. Законы равнопеременного поступательного и вращательного движений. Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению. Криволинейное движение материальной точки считается равномерным движением, если модульскорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении. При движении по криволинейной траектории вектор перемещения
Рис. 1.20. Мгновенная скорость при криволинейном движении. Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – этотангенциальное ускорение:
Где vτ , v0 – величины скоростей в момент времени t0 + Δ t и t0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении. Нормальное ускорение - это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности. Полное ускорение при равнопеременном криволинейном движении тела равно:
Законы равноперемен. поступательного движ. вращательного движений a = const β = const
Принцип инерции и инерциальные системы отсчета. Принцип относительности. Гипотезы и преобразования Галилея. Классический закон сложения скоростей. Инварианты преобразований Галилея. Закон инерции - Всякое тело пребывает в состоянии покоя или прямолинейного равномерного движения до тех пор, пока действующие на него силы не изменят это состояние Инерциальные системы отсчета – с.о., относительно которых выполняется закон инерции, т.е. свободное тело движется равномерно и прямолинейно или покоится. Принцип относительности - в любых инерциальных системах отсчета все механические явления протекают одинаково при одних и тех же условиях. Все инерциальные системы по своим механическим свойствам эквивалентны друг другу. Гипотезы Галилея: 1.Время абсолютно: темп ходов часрв не зависят от их движения. 2. Размеры тел тел не зависят от их движения. Преобразования Галилея – совокупность преобразований моментов времени t и координат x, y, z некоторого события для двух инерциальных систем отсчета: t = t ′ t ′ = t x = x ′ + V 0 t x ′ = x- V t 0 ′ y = y ′ y ′ = y z = z ′ z ′ = z здесь " штрихованная" система отсчета движется поступательно со скоростью 0 V вдоль оси x лабораторной " нештрихованной" системы отсчета.
|

 . Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости
. Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости  определяется скоростью вращения тела
определяется скоростью вращения тела  и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени
и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени  тело повернулось на угол
тело повернулось на угол 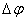 (рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный
(рис 2.4). Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный 








 направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
 или
или 

 n. Вектор нормального ускорения направлен по радиусу кривизны траектории
n. Вектор нормального ускорения направлен по радиусу кривизны траектории

 (не епсилант, а бета)
(не епсилант, а бета)







