Силы и взаимодействия в природе. Масса как мера инертности при поступательном движении тела. Импульс тела. Первый, второй и третий законы Ньютона
Имеется всего четыре типа взаимодействий: гравитационное, электромагнитное, сильное и слабое. Это взаимодействие носит универсальный характер, в нем участвуют все виды материи, все объекты природы, все элементарные частицы. Гравитационное взаимодействие существует между всеми телами, обладающими массами. Закон всемирного тяготения, открытый Ньютоном, гласит: Сила взаимного притяжения двух тел, которые могут быть принятыми за материальные точки, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:
Коэффициент пропорциональности у называют гравитационной постоянной. Она равна 6, 67 • 10-11 Н•м2/кг2. Если на тело действует лишь гравитационная сила со стороны Земли, то она равна mg. Это и есть сила тяжести G (без учета вращения Земли). Сила тяжести действует на все тела, находящиеся на Земле, вне зависимости от их движения. Электромагнитное взаимодействие В электромагнитном взаимодействии участвуют все заряженные тела, все заряженные элементарные частицы. Классической теорией электромагнитного взаимодействия является максвелловская электродинамика. В качестве константы связи принимается заряд электрона e. Если рассмотреть два покоящихся точечных заряда q1 и q2, то их электромагнитное взаимодействие сведется к известной электростатической силе. Это означает, что взаимодействие является дальнодействующим и медленно спадает с ростом расстояния между зарядами. Сильное взаимодействие Сильное взаимодействие ответственно за устойчивость атомных ядер. Поскольку атомные ядра большинства химических элементов стабильны, то ясно, что взаимодействие, которое удерживает их от распада, должно быть достаточно сильным. Хорошо известно, что ядра состоят из протонов и нейтронов. Чтобы положительно заряженные протоны не разлетелись в разные стороны, необходимо наличие сил притяжения между ними, превосходящих силы электростатического отталкивания. Именно сильное взаимодействие является ответственным за эти силы притяжения. Слабое взаимодействие Это взаимодействие является наиболее слабым из фундаментальных взаимодействий, экспериментально наблюдаемых в распадах элементарных частиц, где принципиально существенными являются квантовые эффекты. Слабое взаимодействие в отличие от гравитационного является короткодействующим. Это означает, что слабое взаимодействие между частицами начинает действовать, только если частицы находятся достаточно близко друг к другу. Если же расстояние между частицами превосходит некоторую величину, называемую характерным радиусом взаимодействия, слабое взаимодействие не проявляет себя. Масса Все физические тела обладают свойством инертности (или инерции), которое проявляется в сохранении движения, а также в особенностях изменения его под действием сил. Понятие инерции раскрывается в первом законе Ньютона: " Всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения до тех пор, пока внешние приложенные силы не заставят его изменить это состояние". Говоря проще: тело сохраняет свою скорость, а также под действием внешних сил изменяет ее. Масса - это мера инертности тела при поступательном движении. Она измеряется отношением величины приложенной силы к вызываемому ею ускорению. Масса тела характеризует, как именно приложенная сила может изменить движение тела. Одна и та же сила вызовет большее ускорение у тела с меньшей массой, чем у тела с большей массой.
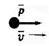
Импульс тела Импульс тела - это физическая векторная величина, равная произведению массы тела на его скорость.
Вектор импульса тела направлен так же как и вектор скорости этого тела.
I Закон ньютона Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго. Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Естественно, результат действия одинаковых по величине сил на различные тела будет различным. Таким образом, говорят, что тела обладают инертностью. Инертность — это свойство тел сопротивляться изменению их текущего состояния. II закон ньютона В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
В случае, когда масса материальной точки меняется со временем, второй закон Ньютона формулируется с использованием понятия импульс: В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил.
III Закон Ньютона Третий закон Ньютона – действие одного тела на другое всегда носит характер взаимодействия, при котором векторы сил одной природы, приложенных к этим телам, равны по величине, противоположны по направлению и лежат на одной прямой.
Импульс системы материальных точек. Вывод уравнения динамики для системы м.т. Центр масс. Уравнение движения центра масс системы материальных точек. Закон сохранения импульса изолированной системы материальных точек. Сохранение отдельных проекций вектора импульса. Механическая система - это совокупность тел, выделенных нами для рассмотрения Внутренние и внешние силы
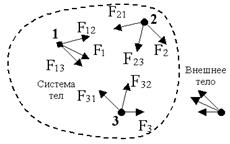
Внутренние силы - силы, с которыми взаимодействуют тела системы между собой. Внешние силы действуют со стороны тел, не входящих в систему. Замкнутая система Импульс системы материальных точек - это векторная сумма импульсов всех материальных точек, входящих в систему
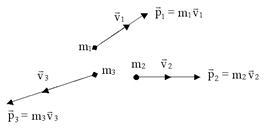
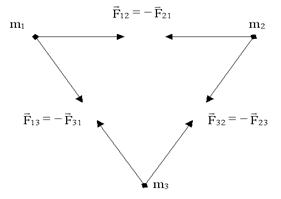
5.2. Закон сохранения импульса Импульс замкнутой системы сохраняется, т.е. не изменяется со временем. На рисунке изображена замкнутая система, состоящая из трех тел.
По II закону Ньютона примененному к каждому телу рассматриваемой замкнутой системы, имеем:
Если система не замкнута, но внешние силы не действуют на неЈ вдоль каких-либо осей, то соответствующие компоненты импульса сохраняются, например:
Центр масс В любой системе частиц имеется одна замечательная точка С - центр инерции, или центр масс
Система центра масс – система отсчета, относительно которой импульс рассматриваемой замкнутой системы материальных точек равен нулю. Центр масс является точкой приложения вектора импульса системы
где центр масс системы совпадает с ее центром тяжести.
где Уравнение движения центра масс: Отсюда следует, что центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы. Для замкнутой изолированной системы тел из 2го закона Ньютона следует что: dР/dt=0 или Р=const Закон сохраниния импульса - полный импульс изолированной механич. Системы с течением времени не изменяется.
Момент импульса материальной точки. Момент силы. Вывод уравнения моментов для материальной точки и системы м.т. Законы сохранения момента импульса изолированной системы материальных точек. Сохранение отдельных проекций вектора момента импульса. Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс материальной точки (рис. 28); L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р. Модуль вектора момента импульса Механическая энергия Лекции по физике
где — угол между векторами r и р, l — плечо вектора р относительно точки О. Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. M=[r, F] (проставить везде векторы) Моментом
Уравнение моментов для м.т. и сисетмы м.т Продефиринцировав
При неподвижной точке О вектор Таким образом 1. Закон сохранения момента импульса. Момент импульса системы относительно произвольного начала сохраняется, если суммарный момент внешних сил относительно этого начала равен нулю.
Работа силы. Потенциальные и непотенциальные силы. Силовое поле. Потенциальная энергия и ее нормировка. Примеры для упругой силы и силы тяжести Земли. Кинетическая энергия. Ее изменение. Закон сохранения механической энергии в нерелятивистском случае Элементарная работа силы F на перемещении точки из одного положения в другое по криволинейной траектории δ A = Fδ s cos (F, v), где δ s – пройденный точкой элементарный путь;
∠ F, v – угол, составленный направлением силы F и скоростью v.
В случае переменной силы определяется элементарная работа на малом перемещении, и после суммирования элементарных работ получается работа силы на конечном перемещении:
Если на частицу действуют одновременно несколько сил, то работа результирующей силы равна сумме работ каждой из действующих сил. Если работа силы не зависит от траектории, а определяется только начальным и конечным положениями материальной точки, то такая сила называется консервативной (или потенциальной). Силы, не удовлетворяющие этому условию, называют неконсервативными. Таковой является сила трения. СИЛОВОЕ ПОЛЕ - часть пространства (ограниченная или неограниченная), в каждой точке к-рой на помещённую туда материальную частицу действует определённая по численной величине и направлению сила, зависящая только от координат х, у, z этой точки. Такое С. п. наз. стационарным; если сила поля зависит и от времени, то С. п. наз. нестационарным; если сила во всех точках С. п. имеет одно и то же значение, т. е. не зависит ни от координат, ни от времени, С. п. наз. однородным. Стационарное С. п. может быть задано ур-ниями где Fx, Fy, Fz - проекции силы поля F. Если существует такая ф-ция U(x, у, z), называемая силовой ф-цией, что элементарная работа сил поля равна полному дифференциалу этой ф-ции, то С. п. наз. потенциальным. В этом случае С. п. задаётся одной ф-цией U(x, у, z), а сила F может быть определена через эту ф-цию равенствами: или или Поверхности U(x, у, z) = const, на к-рых ф-ция сохраняет пост. значение, наз. поверхностями уровня. Сила в каждой точке поля направлена по нормали к проходящей через эту точку поверхности уровня; при перемещении вдоль поверхности уровня работа сил поля равна нулю. Примеры потенциального С. п.: однородное поле тяжести, для к-рого U = -mgz, где т - масса движущейся в поле частицы, g - ускорение силы тяжести (ось z направлена вертикально вверх); ньютоново поле тяготения, для к-рого U = km/r, где r =
Потенциальная энергия Потенциальная энергия
где Кинети́ ческая эне́ ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательногодвижения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленнаядвижением. Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:
Если система замкнута, то есть
остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения. § Если кинетическая энергия может быть определена для одного отдельного тела, то потенциальная энергия всегда характеризует как минимум два тела или положение тела во внешнем поле. § Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел. § Основной физический смысл имеет не само значение потенциальной энергии, а её изменение. Теорема об изменении кинетической энергии системы: в дифференциальной форме: dT = Т2 – Т1= = Nмаш/Nдв, Nмаш – полезная мощность машины, Nдв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение.
|



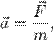

 ,
, 



 рх = const, если Fx = 0,
рх = const, если Fx = 0,  рх = const, если Fx= 0,
рх = const, если Fx= 0,  , так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:
, так как вектор любого импульса является полярным вектором. Положение точки С относительно начала О данной системы отсчета характеризуется радиусом-вектором, определяемым следующей формулой:
 - масса и радиус-вектор каждой частицы системы, M - масса всей
- масса и радиус-вектор каждой частицы системы, M - масса всей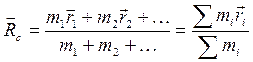 ,
, ,
, .
. где V(c)- скорость движения центра масс
где V(c)- скорость движения центра масс (знак вектора не забудьте поставить над Lrpv)
(знак вектора не забудьте поставить над Lrpv)
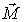 нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки
нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки .
.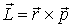 получаем
получаем .
.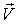 , равный
, равный  , параллелен
, параллелен  и поэтому
и поэтому  . Кроме того
. Кроме того 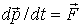 .
.



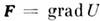 . Условие существования силовой ф-ции для данного С. п. состоит в том, что
. Условие существования силовой ф-ции для данного С. п. состоит в том, что 
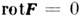 . При перемещении в потенциальном С. п. из точки M1(x1, y1, z1)в точку М2(х2, у2, z2) работа сил поля определяется равенством
. При перемещении в потенциальном С. п. из точки M1(x1, y1, z1)в точку М2(х2, у2, z2) работа сил поля определяется равенством  и не зависит от вида траектории, по к-рои перемещается точка приложения силы.
и не зависит от вида траектории, по к-рои перемещается точка приложения силы. - расстояние от центра притяжения, k - постоянный для данного поля коэффициент. Вместо силовой ф-ции в качестве характеристики потенциального С. п. можно ввести потенциальную энергию П, связанную с U зависимостью П(х, у, z)= = - U(x, у, z). Изучение движения частицы в потенциальном С. п. (при отсутствии других сил) существенно упрощается, т. к. в этом случае имеет место закон сохранения механич. энергии, позволяющий установить прямую зависимость между скоростью частицы и её положением в С. п. с. м. Тарг. СИЛОВЫЕ ЛИНИИ - семейство кривых, характеризующих пространственное распределение векторного поля сил; направление вектора поля в каждой точке совпадает с касательной к С. л. Т. о., ур-ния С. л. произвольного векторного поля А (х, у, z) записываются в виде:
- расстояние от центра притяжения, k - постоянный для данного поля коэффициент. Вместо силовой ф-ции в качестве характеристики потенциального С. п. можно ввести потенциальную энергию П, связанную с U зависимостью П(х, у, z)= = - U(x, у, z). Изучение движения частицы в потенциальном С. п. (при отсутствии других сил) существенно упрощается, т. к. в этом случае имеет место закон сохранения механич. энергии, позволяющий установить прямую зависимость между скоростью частицы и её положением в С. п. с. м. Тарг. СИЛОВЫЕ ЛИНИИ - семейство кривых, характеризующих пространственное распределение векторного поля сил; направление вектора поля в каждой точке совпадает с касательной к С. л. Т. о., ур-ния С. л. произвольного векторного поля А (х, у, z) записываются в виде: 
 — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
— скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
 — масса тела,
— масса тела, 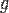 — ускорение свободного падения,
— ускорение свободного падения,  — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
 — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы
— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы  . Учитывая, что
. Учитывая, что 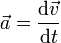 , Получим:
, Получим: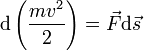
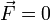 , то
, то  , а величина
, а величина
 ,
, 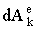 ,
,  – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:
– элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме: . Для неизменяемой системы
. Для неизменяемой системы  и Т2 – Т1=
и Т2 – Т1=  , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд):
, т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд):  < 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.).
< 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.).


