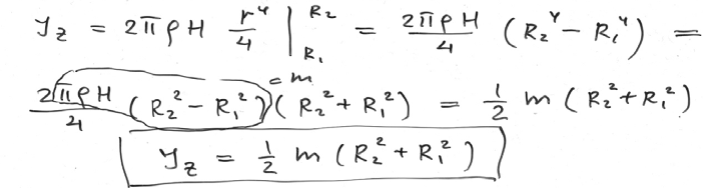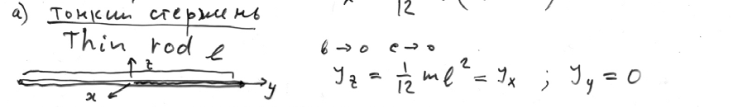Главные оси и главные моменты инерции. Моменты инерции тел простой геометрической формы. Теорема Гюйгенса - Штейнера
ГЛАВНЫЕ ОСИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. u = y sin + x cos ; v = y cos x sin . (3.10) Из выражений: с учетом (3.10) после несложных преобразований получим:
Складывая первые два уравнения, получим: Iu + Iv = Ix + Iy = I , (3.12) где Дифференцируя в (3.11) выражение Iu по и приравнивая его нулю, находим значение = 0 , при котором функция Iu принимает экстремальное значение: С учетом (3.12) можно утверждать, что при = 0 один из осевых моментов Iu или Iv будет наибольшим, а другой наименьшим. Одновременно при = 0 Iuv обращается в нуль, что легко установить из третьей формулы (3.11). Декартовы оси координат, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными и определяются из (3.11) с учетом (3.13) и имеют в В заключение введем понятие радиуса инерции сечения относительно координатных осей x и y ix и iy , соответственно, которые определяются по формулам: МОМЕНТЫ ИНЕРЦИИ ТЕЛ ПРОСТОЙГЕОМЕТРИЧЕСКОЙ ФОРМЫ 1.Момент инерции тонкого кольца относительно оси, проходящей через его центр перпендикулярно его плоскости (или тонкостенного полого цилиндра относительно его оси симметрии): I = mR2
2. Момент инерции диска относительно оси, совпадающей с одним из его диаметров: I = (1/4)mR2.
3. Момент инерции полого цилиндра относительно оси симметрии: I = (1/2)m(R12 + R22)где R1 − внутренний и R2 − внешний радиусы.
5. Момент инерции тонкого стержня относительно оси, проходящей через его середину: I = (1/12)ml2, где l − длина стержня.
7. Момент инерции тонкого шарового слоя: I=(2/3)mR2 8. Момент инерции сплошного цилиндра относительно оси, перпендикулярной к образующей и проходящей через ее середину: I = m(R2/4 + h2/12)где R − радиус основания цилиндра, h − высота цилиндра.
ТЕОРЕМА ГЮЙГЕНСА-ШТЕЙНЕРА момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела Ic относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями: I = Ic + ma2 где Ic — известный момент инерции относительно оси, проходящей через центр масс тела, I — искомый момент инерции относительно параллельной оси, m — масса тела, a — расстояние между указанными осями.
|


 (3.11)
(3.11) ; I полярный момент инерции сечения, величина которого, как видно, не зависит от угла поворота координатных осей.
; I полярный момент инерции сечения, величина которого, как видно, не зависит от угла поворота координатных осей. . (3.13)
. (3.13)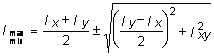 . (3.14)
. (3.14) . (3.15)
. (3.15)