Скорость точки является характеристикой быстроты и направления ее движения
Пусть точка
Отношение приращения дуговой координаты Очевидно, что, чем меньше промежуток времени подходит к величине действительной скорости точки в момент времени Мгновенной Скоростью называется предел Итак, величина скорости точки равна производной от расстояния (дуговой координаты) по времени. Следовательно, она измеряется в единицах длины, отнесенных к единице времени (м/с, см/с). Формула (2.5) определяет величину скорости точки. Чтобы знать не только величину скорости, но и ее направление, введем понятие вектора скорости. Для этого будем определять движение в векторной форме (2.2). В момент времени Отношение приращения радиуса-вектора Направление вектора Из равенства (2.7) следует, что вектор к траектории в точке Итак, вектор скорости точки равен производной от радиуса-вектора по времени. Равенство (2.7) можно представить в виде Вектор Отсюда следует, что определенная равенством (2.5) алгебраическая величина
|
(рис. 2.5, а) движется по криволинейной траектории согласно закону 
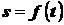. Положим, что в момент времени 
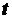точка занимает положение 
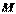, а в момент времени 
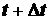положение 
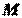, пройдя за время 
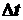путь 
.
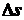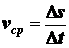(2.4)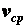
:
; 
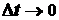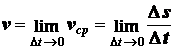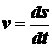. (2.5)
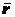, а в момент времени 
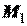, - радиусом-вектором 
.
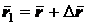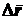к промежутку времени 
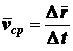(2.6)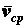
совпадает с направлением вектора 
. 
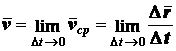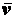всегда направлен по касательной
.
.
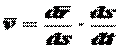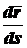, направлен по касательной к траектории в сторону возрастания дуговой координаты 
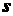и равен по модулю единице. Он называется единичным вектором касательной и обозначается 
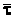. Следовательно, можно записать
.
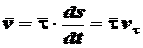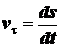представляет собой проекцию вектора скорости 
