Вывод формул для кинетической энергии вращения т.т. вокруг неподвижной оси и для кинетической энергии плоского движения
Вывод формул для кинетической энергии вращения т.т. вокруг неподвижной оси и для кинетической энергии плоского движения. Начнем с рассмотрения вращения тела вокруг неподвижной оси, проходящей чрез него. Мысленно разбив тело на элементарные объемы vi массами mi, находящиеся на расстоянии ri от оси, получим, что скорость элементарной массы определяется выражением vi = ω ⋅ ri (1) Следовательно, для кинетической энергии i-той материальной массы получим (везде где T- это есть кинетическая энергия Ek)
Т.к. мы рассматриваем абсолютно твердое тело, то ω для всех точек выделенного объема массами mi будет одинаково, тогда получим
По определению miri2– момент инерции, получим:
Формула (3) справедлива для тела, вращающегося вокруг неподвижной оси. Плоское движение тела может быть представлено как положение двух движений – поступательного, с некоторой скоростью v0, и вращения вокруг соответствующей оси с угловой скоростью ω. Поэтому, произведя некоторые преобразования, получим
Если ось вращения проходит через центр масс, то rc = 0, следовательно, равна нулю и кинетическая энергия центра масс. Обозначим через vc скорость центра масс, а через Ic момент инерции тела относительно оси, проходящей через центр масс, тогда получим
Формула (5) определяет кинетическую энергию тела при плоском движении, например, цилиндр скатывается по наклонной плоскости.
Столкновения. Законы сохранения при столкновениях. Изображение процессов столкновения с помощью векторных диаграмм на примере упругого столкновения двух частиц. Упругие и неупругие столкновения. Замедление нейтронов как пример упругого столкновения. Передача энергии при столкновениях. СТОЛКНОВЕНИЯ Столкновение – взаимодействие двух или более тел в ограниченной области пространства за ограниченное время, так что вне этой области тела можно считать свободными. При этих взаимодействиях отдельные частицы могут рождаться или уничтожаться. Упругое столкновение – столкновение, при котором внутренние энергии тел не изменяются. Неупругое столкновение – столкновение, при котором внутренние энергии тел изменяются. Абсолютно неупругое столкновение – столкновение, при котором суммарная внутренняя энергия тел увеличивается на максимально возможную величину. ЗАКОНЫ СОХРАНЕНИЯ ПРИ СТОЛКНОВЕНИЯХ Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда неизвестны действующие силы. Примером такого рода задач является ударное взаимодействие тел. Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин. С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике. В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары. Абсолютно неупругий удар - такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело. При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел. Примером абсолютно неупругого удара может служить попадание пули в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рисунок 1). Пуля массой m, летящая горизонтально со скоростью Обозначим скорость ящика с застрявшей в нем пулей через
При застревании пули в песке произошла потеря механической энергии: Отношение
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами. При
Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара. При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии. Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рисунок 2). Центральный удар шаров - соударение, при котором скорости шаров до и после удара направлены по линии центров.
В общем случае массы m 1 и m 2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
Здесь υ 1 – скорость первого шара до столкновения, скорость второго шара υ 2=0, u 1 и u 2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде: m 1υ 1= m 1 u 1+ m 2 u 2. Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u 1 и u 2 шаров после столкновения:
В частном случае, когда оба шара имеют одинаковые массы (m > 1 = m 2), первый шар после соударения останавливается (u 1 = 0), а второй движется со скоростью u 2 = υ 1, то есть шары обмениваются скоростями (и, следовательно, импульсами). Если бы до соударения второй шар также имел ненулевую скорость (υ 2≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ 2 относительно “неподвижной” системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ 1 = υ 1 – υ 2. Определив по приведенным выше формулам скорости u 1 и u 2 шаров после соударения в новой системе, нужно сделать обратный переход к “неподвижной” системе. Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения. Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральномупругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой. Частным случаем нецентрального упругого удара может служить соударения двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рисунок 3).
После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей
Первое из этих равенств означает, что векторы скоростей Замедле́ ние нейтро́ нов — процесс уменьшения кинетической энергии свободных нейтронов в результате их многократных столкновений с атомными ядрами вещества. Вещество, в котором происходит процесс замедления нейтронов, называется замедли́ телем. Замедление нейтронов применяется, например, в ядерных реакторах на тепловых нейтронах. В ходе ядерных реакций, образуются, как правило, быстрые нейтроны (с энергией > 1 МэВ). Быстрые нейтроны при соударениях с атомными ядрами теряют энергию крупными порциями, расходуя её, главным образом, на возбуждение ядер или их расщепление. В результате одного или нескольких столкновений энергия нейтрона становится меньше минимальной энергии возбуждения ядра (от десятков кэВ до нескольких МэВ, в зависимости от свойств ядра). После этого рассеяние нейтрона ядром становится упругим, то есть нейтрон расходует энергию на сообщение ядру скорости без изменения его внутреннего состояния. При одном упругом соударении нейтрон теряет, в среднем, долю энергии, равную ПЕРЕДАЧА ЭНЕРГИИ ПРИ СТОЛКНОВЕНИЯХ Рассматривая изменение кинетической энергии шаров в результате удара, можно убедиться, что в случае равных масс происходит полный обмен энергией, в то время как при большой разнице в массах снаряд при столкновении может передать мишени лишь малую часть своей энергии. В самом деле, пусть, например, снаряд много легче мишени. Тогда, пренебрегая в знаменателе формулы для величиной по сравнению, получаем, откуда для кинетической энергии мишени после удара имеем Аналогичный результат получится и в случае, если снаряд значительно тяжелее мишени В действительности лобовой удар это большая редкость. Его относительно легко осуществить разве что при игре в бильярд, а при столкновении молекул, атомов и элементарных частиц подавляющее число ударов являются нецентральными. Если частица налетает на неподвижную частицу такой же массы, то при нецентральном упругом ударе частицы разлетаются под прямым углом друг к другу. Действительно, законы сохранения импульса и энергии принимают вид Первое из этих равенств означает, что векторы скоростей образуют треугольник, а второе что для этого треугольника справедлива теорема Пифагора, он прямоугольный: угол между. Векторы, скоростей частиц с одинаковыми массами, разлетающихся после упругого удара, направлены под прямым углом друг к другу; греки в пузырьковой камере (или камере Вильсона) при столкновении быстрого протона с неподвижным катетами равен. Однако законов сохранения энергии и импульса недостаточно для определения направления векторов относительно направления движения налетающей частицы. Для того чтобы определить эти направления, нужно знать закон взаимодействия между частицами и их взаимное положение в момент столкновения.
|






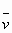 , попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.
, попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули. Тогда по закону сохранения импульса
Тогда по закону сохранения импульса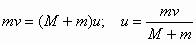
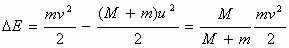
 называется долей кинетической энергии пули, перешедшая во внутреннюю энергию системы:
называется долей кинетической энергии пули, перешедшая во внутреннюю энергию системы:
 почти вся кинетическая энергия пули переходит во внутреннюю энергию. При
почти вся кинетическая энергия пули переходит во внутреннюю энергию. При  во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m > > М) отношение
во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m > > М) отношение  Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии: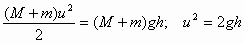 где h – максимальная высота подъема маятника. Из этих соотношений следует:
где h – максимальная высота подъема маятника. Из этих соотношений следует: 
 Рисунок 1Абсолютно упругий удар - столкновение, при котором сохраняется механическая энергия системы тел.
Рисунок 1Абсолютно упругий удар - столкновение, при котором сохраняется механическая энергия системы тел. Рисунок 2.
Рисунок 2.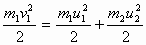

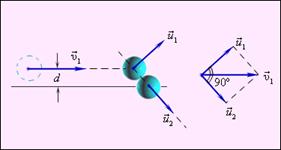 Рисунок 3
Рисунок 3 и
и  после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рисунок 3), то есть расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости
после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рисунок 3), то есть расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости  налетающего шара. Если массы шаров одинаковы, то векторы скоростей
налетающего шара. Если массы шаров одинаковы, то векторы скоростей 
 где А — массовое число ядра-мишени. Эта доля мала для тяжёлых ядер (1/100 для свинца) и велика для лёгких ядер 1/7 для углерода и 1/2 для водорода). Поэтому замедление нейтронов происходит на лёгких ядрах гораздо быстрее, чем на тяжёлых.
где А — массовое число ядра-мишени. Эта доля мала для тяжёлых ядер (1/100 для свинца) и велика для лёгких ядер 1/7 для углерода и 1/2 для водорода). Поэтому замедление нейтронов происходит на лёгких ядрах гораздо быстрее, чем на тяжёлых.


