Расчеты на прочность при растяжении и сжатии. При растяжении и сжатии напряжения по площади поперечного сечения распределяются равномерно

При растяжении и сжатии напряжения по площади поперечного сечения распределяются равномерно. Следствием этого расчет на прочность статически определимых систем по допускаемым напряжениям и по предельным состояниям дает одинаковый результат. В случае статически неопределимых систем происходит перераспределение напряжений и результаты разнятся.

Возьмем пример статически неопределимой системы (рис. 3.4.). Реакции равны B = 2/3F и C = 1/3F. Поэтому в левой части стержня будет напряжение:

,

в правой части:

,

где А - площадь поперечного сечения;

F - внешняя сила.

При расчете по допускаемым напряжениям критическое состояние наступит, когда в левой части напряжения достигнут s_т. (не допускаются пластические деформации). В левой части напряжения в 2 раза выше, чем в правой. Следовательно, стержень может воспринять предельную нагрузку F_y:

F_y = s_Т A + 1/2 s_Т A = 3/2s_Т A.

При расчете по предельному состоянию допускаются пластические деформации. Из-за, пластических деформаций напряжения в левой и правой частях стержня будут выравниваться. Предельное состояние наступит, когда напряжение в них будет равно s .

Тогда предельная нагрузка F_пр равна

F_пр=s_т А + s_т А=2s_т А.

Определим, во сколько раз предельная нагрузка, рассчитанная по предельному состоянию, больше нагрузки, рассчитанной по допускаемым напряжениям:

.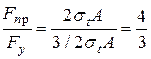