Формула Эйлера для критической силы
Рассмотрим сжатый стержень в критическом состоянии, т.е. когда он слегка прогнулся (см. рис. 15.1). В произвольном сечении, взятом на расстоянии z от левого конца стержня, изгибающий момент от критической силы
где
Рис.15.1 Знак " минус" взят потому, что стержень изгибается концами вниз. Если бы стержень прогнулся дугой вниз, то момент был бы положительным, но прогиб Согласно формуле (11.1), дифференциальное уравнение изогнутой оси стержня примет вид:
При сжатии вдоль оси стержень всегда изгибается относительно той оси, момент инерции относительно которой минимальный. В этом можно убедиться, сжимая линейку. Поэтому в формуле (15.1) берем минимальный осевой момент инерции сечения. Преобразуем уравнение (15.1):
Обозначив
получим:
Это линейное дифференциальное уравнение второго порядка. Его решение имеет вид:
Для определения произвольных постоянных А и В используем граничные условия. При z = 0; y = 0; Уравнение примет вид:
Как видно из уравнения (15.5), стержень изогнется по синусоиде. Второе граничное условие: При z = l; y = 0; Это условие выполняется в двух случаях: 1) B = 0; 2) Первый случай отбрасываем, так как при нем прогибы всех точек равны нулю, т.е. стержень остается прямым. При втором случае:
Возьмем общий случай: Возведем в квадрат обе части уравнения:
Вместо
или
Принимая
Критическая сила зависит от способа закрепления концов стержня, поэтому вводится коэффициент
Значения коэффициента
Рис. 15.2
|

 равен:
равен:
 - прогиб стержня.
- прогиб стержня.
 было бы все равно со знаком " минус".
было бы все равно со знаком " минус".





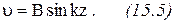
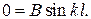
 = 0.
= 0.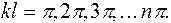


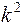 подставим его значение из формулы (15.2):
подставим его значение из формулы (15.2):

 = 1,
= 1, 
 - коэффициент приведенной длины (не путать с коэффициентом поперечной деформации). В общем случае формула Эйлера примет вид:
- коэффициент приведенной длины (не путать с коэффициентом поперечной деформации). В общем случае формула Эйлера примет вид:




