Кручение с изгибом
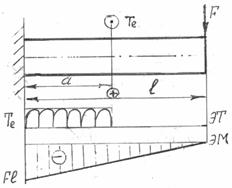
Рассмотрим случай совместного действия кручения и изгиба на стержень круглого сечения (см. рис. 14.9). Определим внутренние усилия и построим их эпюры. Крутящий момент будет возникать на участке от заделки стержня до сечения, где приложен внешний момент
Принимаем это направление Т за положительное (четких правил знаков для крутящих моментов нет) и строим эпюру Т. От силы F будет возникать изгибающий момент, наибольшее значение которого будет в заделке: M = - Fl.
Рис.14.9 Строим эпюру изгибающих моментов. Из эпюр Т и М видно, что опасное сечение будет в заделке. Поэтому расчет на прочность будем проводить для этого сечения. Для опасного сечения определим напряжения и построим их эпюры (см. рис. 14.10).
Рис.14.10 Согласно формулам (9.1) и (9.2):
и формулам (10.3) и (10.6):
Опасными будут точки 1 и 2. Для них и нужно составить условие прочности, т.е. учитывать
Рис. 14.11 Главные напряжения определяют по формуле (6.11):
В данном случае
У главных напряжений обязательно
Валы, как правило, изготавливают из стали, т.е. пластичного материала. Для пластичного материала можно применить гипотезу наибольших касательных напряжений (формула 13.5):
Подставив значения
Вместо
Для круглого сечения согласно формулам (10.9) и (9.3) имеем:
В формуле (14.17) заменим
Если использовать энергетическую гипотезу прочности, то получим:
Формула (14.19) отличается от формулы (14.16) только тем, что в ней
Формулы (14.18) и (14.20) используют для расчетов валов, работающих на кручение и изгиб.
|

 :
: .
.



 . Индексы max в дальнейшем опустим, чтобы упростить написание. Поскольку в опасной точке возникает касательное и нормальное напряжения, то непосредственно, как в случаях косого изгиба или внецентренного растяжения, составить условие прочности нельзя. Нужно вначале определить главные напряжения и затем использовать соответствующую для данного материала теорию прочности. Определим главные напряжения. В поперечном сечении возникают касательные напряжения
. Индексы max в дальнейшем опустим, чтобы упростить написание. Поскольку в опасной точке возникает касательное и нормальное напряжения, то непосредственно, как в случаях косого изгиба или внецентренного растяжения, составить условие прочности нельзя. Нужно вначале определить главные напряжения и затем использовать соответствующую для данного материала теорию прочности. Определим главные напряжения. В поперечном сечении возникают касательные напряжения  и нормальные
и нормальные  . Согласно закону парности касательных напряжений, в продольных сечениях будут возникать касательные напряжения, равные по величине и обратные по знаку (закон парности касательных напряжений). Элемент представлен на рис. 14.11.
. Согласно закону парности касательных напряжений, в продольных сечениях будут возникать касательные напряжения, равные по величине и обратные по знаку (закон парности касательных напряжений). Элемент представлен на рис. 14.11.
 .
.
 .
. Поэтому:
Поэтому:
 .
. , получим:
, получим:
 подставим их максимальные значения:
подставим их максимальные значения:

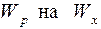 :
:

 , а не
, а не  . Поэтому можно сразу записать окончательную формулу:
. Поэтому можно сразу записать окончательную формулу:



