Теория трещиностойкости Гриффитса
В любом реальном материале могут существовать как многочисленные несовершенства структуры (поры, трещины, микротрещины, внедренные атомы примесей), так и остаточные деформации. Поэтому реальная прочность материала в сотни раз меньше теоретической. Тело с трещиной условно представим в виде пластины единичной толщины, в которой имеется сквозная прямолинейная щель длиной 2 l (см. рис 13.1), поскольку трещина может развиваться в обе стороны. Длина трещины мала по сравнению с размерами пластины.
Рис. 13.1 Исходя из точного решения задачи теории упругости о растяжении пластины с эллиптическим отверстием при стремлении малой полуоси эллипса к нулю, Гриффитс получил формулу:
где 2 Из выражения (13.9) следует:
т.е. для данного материала Гриффитс считал, что для развития трещины необходимо, чтобы приращение освобождаемой потенциальной энергии деформации из-за роста трещины превышало приращение поверхностной энергии:
Потенциальная энергия деформации, согласно формуле (6.14):
где E - модуль продольной упругости,
В данном случае выше и ниже трещины будут слои материала (заштриховано на рисунке), где напряжения ниже, чем
где Потенциальная энергия, освобождаемая из-за образования трещины, равна:
Взяв производную по l, получим:
Для того, чтобы создать трещину, нужно совершить работу по отрыву частиц одна от другой. Эта работа пропорциональна длине трещины:
Первая производная от работы W по длине l:
Из условия (13.12) получим:
или, приняв
По формуле (13.14) определяется критическая длина трещины. Эксперименты, проводимые Гриффитсом со стеклянными нитями, дали положительные результаты. Однако, для не столь хрупких материалов, как стекло, развитие трещины сопровождается пластическими деформациями по краям, на что дополнительно затрачивается энергия. Ученые Орован и Ирвин доказали, что модель Гриффитса рассматривания трещины справедлива и при наличии малой зоны пластических деформаций. Тогда константа
В этом случае продвижение трещины называют квазихрупким разрушением (слово " квази" означает " как бы"). Возможны три вида раскрытия трещин: 1. отрыв (см. рис. 13.2 а); 2. плоский сдвиг (см. рис. 13.2 б); 3. антиплоский сдвиг (рис. 13.2 в).
Рис.13.2 Соответственно виду раскрытия трещины для коэффициента интенсивности напряжений даются индексы:
Условие устойчивости трещины для первого случая можно записать в виде неравенства:
Из зависимости (13.11) получим:
откуда найдем связь между критическим напряжением
Формула (13.16) позволяет также определить безопасный при данном напряжении размер трещины:
|



 - поверхностное натяжение или удельная энергия, необходимая, чтобы разорвать связи между частицами материала и удлинить трещину;
- поверхностное натяжение или удельная энергия, необходимая, чтобы разорвать связи между частицами материала и удлинить трещину; - длина равновесной трещины.
- длина равновесной трещины.
 - величина постоянная, характеризующая свойство материала по отношению к трещинообразованию, называемая критическим коэффициентом интенсивности напряжений. Если длина трещины
- величина постоянная, характеризующая свойство материала по отношению к трещинообразованию, называемая критическим коэффициентом интенсивности напряжений. Если длина трещины  , то трещина самопроизвольно удлиняется. Для того, чтобы трещина не развивалась, нужно, чтобы
, то трещина самопроизвольно удлиняется. Для того, чтобы трещина не развивалась, нужно, чтобы  . Коэффициент
. Коэффициент  называют коэффициентом интенсивности напряжений. Его размерность
называют коэффициентом интенсивности напряжений. Его размерность  . Поэтому условие трещиностойкости будет иметь вид:
. Поэтому условие трещиностойкости будет иметь вид: 

 ,
, - объем тела.
- объем тела. , а на поверхности трещины они вообще отсутствуют. Поэтому точно определить объем тела, где исчезают и уменьшаются напряжения, весьма сложно. Очевидно, что этот объем будет пропорционален квадрату длины трещины:
, а на поверхности трещины они вообще отсутствуют. Поэтому точно определить объем тела, где исчезают и уменьшаются напряжения, весьма сложно. Очевидно, что этот объем будет пропорционален квадрату длины трещины:
 - коэффициент.
- коэффициент.
 .
.
 .
.
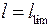 , находим:
, находим: =
=  . (13.14)
. (13.14) . Работа
. Работа  , затрачиваемая на хрупкое разрушение межатомных связей, значительно меньше работы пластической деформации
, затрачиваемая на хрупкое разрушение межатомных связей, значительно меньше работы пластической деформации  :
:

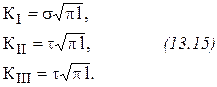

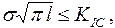
 и критическим размером трещины
и критическим размером трещины 
 .
.


