Косой изгиб. Изгиб называют косым, если плоскость изгибающего момента не проходит ни через одну из главных осей сечения
Изгиб называют косым, если плоскость изгибающего момента не проходит ни через одну из главных осей сечения. Пусть к свободному концу стержня приложена сила F, не совпадающая ни с одной из главных осей и проходящая через центр тяжести сечения (рис. 14.1). Если направление силы не будет проходить через центр тяжести, то, помимо изгибающих, будет создаваться и крутящий момент. Этот случай мы рассмотрим чуть позднее.
Рис.14.1 По правилу параллелограмма разложим силу F на составляющие
т.е. косой изгиб наблюдается, когда в сечении возникают два изгибающих момента. Из формул (14.1) следует, что значения изгибающих моментов прямо пропорциональны z. При z = 0; Для опасного сечения АВСД (см. рис. 14.2) определим напряжения и построим их эпюры. От изгибающего момента возникают нормальные напряжения, определяемые по формулам (10.3) и (10.6):
От изгибающего момента
Рис. 14.2 От момента
Эпюру Условие прочности для опасной точки будет иметь вид:
Для определения перемещений определяют отдельно прогибы от Мх и Му и по их сумме определяют общий прогиб: f = где U и V - соответственно прогибы от Мy и Мx.
|

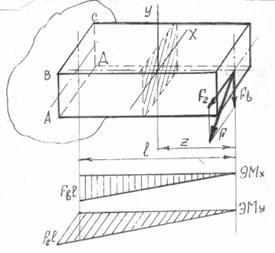
 , перпендикулярные, соответственно, осям X и Y. В произвольном сечении на расстоянии z от правого конца балки будут возникать изгибающие моменты:
, перпендикулярные, соответственно, осям X и Y. В произвольном сечении на расстоянии z от правого конца балки будут возникать изгибающие моменты: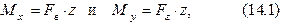
 и при z = l
и при z = l  . Строим эпюры моментов
. Строим эпюры моментов 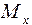 и
и 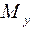 . Момент
. Момент 



 строим справа от сечения, эпюру
строим справа от сечения, эпюру  - внизу. Анализируя эпюры
- внизу. Анализируя эпюры  , видим, что наибольшие растягивающие напряжения будут возникать в точке С, а сжимающие - в точке А (опасные точки).
, видим, что наибольшие растягивающие напряжения будут возникать в точке С, а сжимающие - в точке А (опасные точки).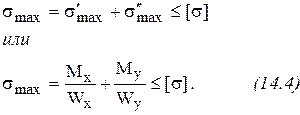
 ,
,


