Внецентренное растяжение (сжатие)
В реальных условиях часто сжимающая или растягивающая сила приложены не в центре тяжести сечения, а с каким-то смещением, например, на рисунке 14.5а, точка приложения силы F имеет координаты
Рис.14.5 Возьмем произвольное сечение на высоте Z (оно заштриховано) и определим внутренние усилия. Силу F можно перенести в центр сечения, но при этом нужно добавить два момента (см. рис. 14.5 б):
Сила F, приложенная к центру сечения, вызовет продольную силу, равную ей: N=F.
Поскольку внутренние усилия не зависят от z (высота сечения), то в любом сечении они будут одинаковы. Можно сказать, что все сечения стержня равноопасны. Определим напряжения от каждого внутреннего усилия и построим их эпюры. От продольной силы N возникают нормальные напряжения, одинаковые во всех точках сечения:
От изгибающих моментов
Эпюры нормальных напряжений представлены на рисунке 14.6.
Рис.14.6 Из эпюр напряжений видно, что наибольшие напряжения возникают в точке С (опасная точка). Для нее составим условие прочности:
Составим уравнение нулевой линии, т.е. линии, на которой суммарные напряжения равны нулю:
или, подставив формулы (14.6-14.8), получим:
Внутренние силы выразим через внешнюю силу F: N = F;
или
Заменим
где Окончательно уравнение нулевой линии примет вид:
Это уравнение прямой в отрезках, так как эта прямая отсекает отрезки на осях X и Y соответственно знаменателям под переменными. Так, при x=0, Все полученные зависимости справедливы и для случая внецентренного сжатия. Некоторые материалы (кирпичная и каменная кладка, грунт) не могут сопротивляться растягивающим усилиям. Поэтому при внецентренном сжатии нельзя допустить, чтобы какие-либо точки сечения испытывали растяжение. В этой связи важно определить зону приложения нагрузки (ядро сечения), обеспечивающую во всех точках сечения только сжатие.
|

 .
.
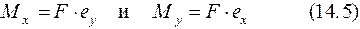

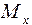 и
и 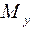 , соответственно:
, соответственно: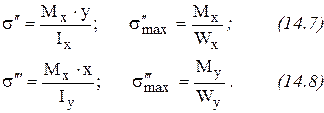




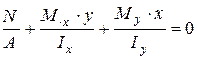 .
. . Тогда получим:
. Тогда получим: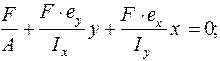

 , (14.10)
, (14.10) - радиусы инерции сечения, м.
- радиусы инерции сечения, м.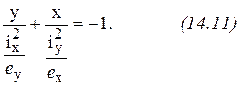
 а при y=0,
а при y=0, 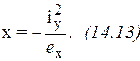 . Поскольку в этих формулах стоит знак " минус", то y и
. Поскольку в этих формулах стоит знак " минус", то y и 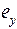 , а также x и
, а также x и  лежат по разные стороны от центра тяжести сечения.
лежат по разные стороны от центра тяжести сечения.


