Пенроуз Р. 17 страница
17.6. Тонкостенный цилиндр с диаметром основания D = 30 см и массой m = 12 кг вращается согласно уравнению φ = A+Bt+Ct3, где A = 4 рад; B = –2 рад/с; C = 0, 2 рад/с3. Определить действующий на цилиндр момент сил M в момент времени t = 3 с.
17.8. Однородный стержень длиной 1, 5 м и массой 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня перпендикулярно его длине. В середину стержня ударяет пуля массой 10 г, летящая в горизонтальном направлении со скоростью 500 м/с, и застревает в стержне. Какую линейную скорость будет иметь конец стержня сразу после удара?
17.9. Маховик массой 4 кг свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой 720 мин-1. Массу маховика можно считать распределенной по его ободу радиусом 40 см. Какую работу совершат силы торможения при остановке маховика?
17.10. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Какой из цилиндров поднимется выше и во сколько раз, если начальные скорости тел одинаковы?
ИДЗ «Механика вращательного движения твердого тела»
Вариант 18
18.2. Твердое тело вращается вокруг неподвижной оси по закону
18.4. Три точечных массы каждая по 100 г, образуют равносторонний треугольник со стороной 10 см. Вычислить момент инерции всей системы относительно оси, расположенной в плоскости, в которой лежат все массы, и проходящей через одну из сторон треугольника.
18.6. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 с приобрел угловую скорость ω = 9 рад/с.
18.7. Момент импульса тела относительно неподвижной оси изменяется по закону
18.8. Платформа в виде диска вращается по инерции около вертикальной оси с частотой n 1 = 14 мин -1. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до n 2 = 25 мин -1. Масса человека m = 70 кг. Определить массу платформы. Момент инерции человека рассчитывать, как для материальной точки.
18.9. Тонкостенный цилиндр с диаметром основания D = 30 см и массой m = 12 кг вращается согласно уравнению φ = A+Bt+Ct3, где A = 4 рад; B = - 2 рад/с; C =0, 2 рад/с 3. Какую работу А совершит внешняя сила за t = 2 с?
18.10. Обруч и диск одинаковой массы m1 = m 2= 1 кг катятся по горизонтальной поверхности без скольжения с одинаковой скоростью V1 = V2 = 18 км/ч. Радиус обруча в два раза больше чем диска. Кинетическая энергия обруча = 40 Дж. Определите кинетическую энергию диска.
ИДЗ «Механика вращательного движения твердого тела» Вариант 19
19.1. На рисунке стрелками показаны направления углового ускорения и направления вращения дисков. Какой из дисков вращается равнозамедленно?
19.4. Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы и равны 10 см. Массы шариков слева направо: m1 = 1 г, m2 = 2 г, m3 = 3 г m4 = 4 г m1 = 1 г 2 г, 3 г,
19.5. На рисунке показаны начальная вызывающий вращение данного тела?
19.6. Тонкий однородный стержень длиной l = 0, 5 м и массой m = 400 г вращается с угловым ускорением ε = 3 рад/с 2 около оси, проходящей перпендикулярно стержню через его середину. Определите вращающий момент М.
19.9. Маховик вращается вокруг по закону, выраженному уравнением φ = 2+32 t-4t2, рад. Найдите среднюю мощность, развиваемую силами действующими на маховикпри его движении до остановки, если его момент инерции J = 100 кг∙ м2.
19.10. Сплошной однородный диск катится по горизонтальной плоскости со скоростью v=10 м/с. Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен 0, 02.
ИДЗ «Механика вращательного движения твердого тела»
Вариант 20
20.2. Диск вращается вокруг неподвижной оси по закону
20.6. Стержень вращается вокруг оси, проходящей через его один из его концов согласно уравнению φ = At+Bt3, где A =2 рад/с; B = 0, 2 рад/с3. Найдите закон изменения момента сил M, действующих на стержень. Определите угловую скорость и момент сил M в момент времени t = 2 с, если момент инерции стержня J = 0, 048 кг∙ м2.
20.7. Момент силы, приложенный к вращающемуся телу, изменяется по закону Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке …
20.8. Человек стоит на скамье Жуковского, вращающейся с пренебрежимо малым трением, и бросает ручной мяч массой m = 0, 4 кг в горизонтальном направлении со скоростью v = 20 м/с. Траектория мяча проходит на расстоянии r = 0, 8 м от вертикальной оси вращения скамьи. С какой угловой скоростью ω начнет вращаться скамейка Жуковского с человеком после броска мяча? Считать, что суммарный момент инерции человека и скамьи J = 6 кг∙ м2.
20.9. Маховик вращается с частотой n = 900 об/мин. После выключения двигателя маховик, вращаясь равнозамедленно, сделал до остановки N=75 об. Работа сил торможения А = 44, 4 Дж. Найти момент инерции I маховика и момент сил торможения М.
20.10. Столб высотой h = 3, 0 м и массой m = 50, 0 кг из вертикального положения падает на землю. Определите момент количества движения L относительно точки опоры и скорость верхнего конца столба в момент удара о землю.
Пенроуз Р.
|

 17.4. Определите во сколько раз изменится момент инерции тонкого однородного стержня, если ось вращения стержня перенести из центра масс на один из его концов (см рисунок)?
17.4. Определите во сколько раз изменится момент инерции тонкого однородного стержня, если ось вращения стержня перенести из центра масс на один из его концов (см рисунок)? 17.5. На невесомом стержне укреплены два шарика, размерами которых можно пренебречь. Массы шариков и соответствующие расстояния указаны на рисунке
17.5. На невесомом стержне укреплены два шарика, размерами которых можно пренебречь. Массы шариков и соответствующие расстояния указаны на рисунке  Наибольший момент инерции такой системы будет относительно оси, приведенной на рисунке под номером …
Наибольший момент инерции такой системы будет относительно оси, приведенной на рисунке под номером … 17.7. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке.
17.7. Диск начинает вращаться под действием момента сил М, график временной зависимости которого представлен на рисунке. Укажите график, правильно отражающий зависимость угловой скорости диска от времени.
Укажите график, правильно отражающий зависимость угловой скорости диска от времени. 18.1. Диск вращается равноускоренно вокруг вертикальной оси под действием силы F. Вектор угловой скорости обозначен цифрой …
18.1. Диск вращается равноускоренно вокруг вертикальной оси под действием силы F. Вектор угловой скорости обозначен цифрой … , рад. Найдите угловое ускорение в момент остановки и среднее значение углового ускорения за промежуток времени от t = 0 до момента остановки.
, рад. Найдите угловое ускорение в момент остановки и среднее значение углового ускорения за промежуток времени от t = 0 до момента остановки.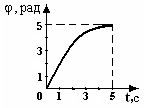 18.3. На графике представлена зависимость угла поворота φ абсолютно твердого тела, вращающегося вокруг неподвижной оси, от времени t. Найдите величину угловой скорости вращения в начальный момент времени.
18.3. На графике представлена зависимость угла поворота φ абсолютно твердого тела, вращающегося вокруг неподвижной оси, от времени t. Найдите величину угловой скорости вращения в начальный момент времени. 18.5. Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Массы шариков
18.5. Четыре шарика, размеры которых пренебрежимо малы, движутся по окружностям с одинаковой угловой скоростью. Массы шариков  и радиусы окружностей
и радиусы окружностей  указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика …
указаны на рисунках. Момент импульса относительно оси, проходящей через центр окружности, максимален у шарика … . Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
. Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.

 19.2. Движение тела с неподвижной осью вращения, расположенной перпендикулярно плоскости рисунка, задано уравнением
19.2. Движение тела с неподвижной осью вращения, расположенной перпендикулярно плоскости рисунка, задано уравнением  , рад. Начало движения при
, рад. Начало движения при 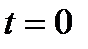 . Положительные углы отсчитываются в направлении стрелки на рисунке. С какой скоростью и в каком направлении будет вращаться в тело момент времени
. Положительные углы отсчитываются в направлении стрелки на рисунке. С какой скоростью и в каком направлении будет вращаться в тело момент времени  с после начала движения?
с после начала движения? 19.3. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Максимальное по модулю угловое ускорение соответствует участку …
19.3. На рисунке приведен график зависимости от времени проекции угловой скорости вращающегося тела на ось вращения. Максимальное по модулю угловое ускорение соответствует участку … 4 г. Найдите во сколько раз изменится момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы, если поменять местами шарики 2 и 3.
4 г. Найдите во сколько раз изменится момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы, если поменять местами шарики 2 и 3.
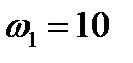 рад/с и конечная
рад/с и конечная  рад/с скорости вращения абсолютно твердого тела для интервала времени
рад/с скорости вращения абсолютно твердого тела для интервала времени  . Как направлен момент сил,
. Как направлен момент сил, 19.7. На рисунке приведен график зависимости проекции угловой скорости вращающегося тела на ось вращения от времени. Как изменяется модуль вращающего момента сил. действующего на тело, на интервале времени от
19.7. На рисунке приведен график зависимости проекции угловой скорости вращающегося тела на ось вращения от времени. Как изменяется модуль вращающего момента сил. действующего на тело, на интервале времени от  до
до  ?
? 19. 8. Однородный стержень длиной 1, 0 м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О. В точку А на стержне попадает пластилиновый шарик, летящий горизонтально со скоростью = 10 м/с и прилипает к стержню. Масса шарика =10г. Определите угловую скорость стержня и линейную скорость конца стержня сразу после прилипания шарика.
19. 8. Однородный стержень длиной 1, 0 м может свободно вращаться вокруг горизонтальной оси, проходящей через точку О. В точку А на стержне попадает пластилиновый шарик, летящий горизонтально со скоростью = 10 м/с и прилипает к стержню. Масса шарика =10г. Определите угловую скорость стержня и линейную скорость конца стержня сразу после прилипания шарика. 20.1. Диск вращается равноускоренно вокруг вертикальной оси против часовой стрелки (если смотреть сверху). Вектор углового перемещения обозначен цифрой …
20.1. Диск вращается равноускоренно вокруг вертикальной оси против часовой стрелки (если смотреть сверху). Вектор углового перемещения обозначен цифрой … , рад. Определите среднее значение угловой скорости за время движения до остановки и число оборотов N, сделанных за это время.
, рад. Определите среднее значение угловой скорости за время движения до остановки и число оборотов N, сделанных за это время. 20.4. Определите момент инерции системы, состоящей из четырех точечных масс m1 = 1 г, m2 = 2 г, m3 = 3 г m4 = 4 г, расположенных по вершинам квадрата со стороной а, относительно оси, расположенной перпендикулярно плоскости квадрата, и проходящей через точку, в которой расположена вторая масса m2.
20.4. Определите момент инерции системы, состоящей из четырех точечных масс m1 = 1 г, m2 = 2 г, m3 = 3 г m4 = 4 г, расположенных по вершинам квадрата со стороной а, относительно оси, расположенной перпендикулярно плоскости квадрата, и проходящей через точку, в которой расположена вторая масса m2. 20.5. Равнозамедленное вращение совершает диск, приведенный на рисунке под номером …
20.5. Равнозамедленное вращение совершает диск, приведенный на рисунке под номером … , где
, где  – некоторая положительная константа.
– некоторая положительная константа.



