ПРОЦЕСС РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ В КАКОЙ-ЛИБО СРЕДЕ НАЗЫВАЕТСЯ ВОЛНОЙ

В результате распространения волны частицы будут совершать колебания около своего положения равновесия. При этом происходит передача энергии без переноса вещества.

Если колебания частиц происходят в том же направлении, что и распространение энергии, волны называют продольными. При этом в ряду частиц образуются последовательные сгущения и разряжения, т.е. изменение плотности, которые распространяются с конечной скоростью. Продольные волны распространяются в жидких и газообразных средах.

Если колебания частиц перпендикулярны направлению распространения волны (энергии), то такие волны называют поперечными. При этом в ряду частиц образуются последовательные горб и впадина. Поперечные волны распространяются в твердых телах и на границе жидкость-газ.

Достигнув нашего органа слуха, колебания с частотой от 20 Гц до 20 кГц вызывают специфические ощущения звука и могут быть выделены по этому признаку в особую группу звуковых (акустических) колебаний.

Поперечные и продольные волны описываются одинаковыми уравнениями.

 

2. УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ

 

Если не имеет место затухание колебаний, в волне все частицы совершают колебания в одном и том же направлении, с одним и тем же периодом и одной и той же амплитудой. Однако колебания каждой частицы отстают по фазе от колебаний предыдущей частицы. Расстояние между двумя ближайшими частицами, которые колеблются в одинаковой фазе, называется длиной бегущей волны. Можно также сказать: длиной бегущей волны называют расстояние, на которое смещается волна за время, равное периоду:

,

 

Здесь - длина волны, V- скорость её распространения, T- период колебаний.

Рассмотрим процесс распространения колебаний, источник которого расположен в начале координат и дает гармонические колебания. Пусть начальная фаза колебаний :

 

у=у_мsin = у_мsin

 

Для точки, находящейся от начала координат на расстоянии х, можно записать такое же уравнение, но необходимо принять во внимание, что колебания в ней будут начинаться позднее на время , необходимое волне пройти расстояние х: . Таким образом, для величины смещения у в момент времени t можно записать:

у=у_мsin (t- 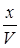)=у_мsin2 ( - )=y_мsin(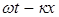); где к= - волновое число. Это выражение называется уравнением бегущей волны.

6. ЯВЛЕНИЕ ИНТЕРФЕРЕНЦИИ