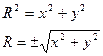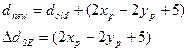Растровые алгоритмы построения окружности

 

Окружность, как и отрезок, можно построить в лоб, используя математическое представление:

Тогда для каждого значения по оси абсцисс мы сможем вычислить соответствующее ему значение по ординате и поставить точку.

У данного метода существует несколько недостатков:

- Слишком сложные вычисления (операция извлечения корня квадратного)

- Пиксели неравномерно распределяются по окружности, и она оказывается неравномерно освещенной

 

От второго недостатка можно избавиться, если использовать представление окружности в полярных координатах:

Тогда, пробегая все возможные значения q с заданным шагом, для каждого из них мы определим координаты соответствующего ему пиксела, и закрасим его. На этот раз, т.к. мы каждый раз поворачиваем радиус на один и тот же угол, то пикселы будут равномерно распределены по окружности (рис.5). Однако, как и в предыдущем алгоритме, вычисление операции cos и sin слишком трудоёмки.

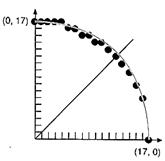
Задачу можно значительно упростить, если использовать то, что окружность является центрально-симметричной фигурой, а значит, если построить, к примеру, одну восьмую ее часть, то с помощью преобразования симметрии, можно достроить окружность полностью (рис.6).

 

Тогда можно использовать метод срединной точки для построения дуги окружности. Если за первый в дуге взять самый верхний пиксел, то следующим может быть лишь Е или SE пиксел. И это справедливо для каждого пиксела в дуге. Если линия проходит выше срединной точки, то следующим пикселом будет E, если ниже – то SE.

Как и в случае отрезка, будем использовать задание окружности в неявном виде с помощью функции F(x, y):

Если F=0, то точка с данными координатами (x, y) расположена на окружности, если больше нуля – то вне окружности. А если меньше нуля – то внутри окружности.

Пусть поставленная точка имеет координаты:

Вычислим значение в соответствующей ей срединной точке:

Если это d меньше нуля, т.е. окружность проходит выше срединной точки, то выбирается пиксел E, иначе выбирается пиксел SE.

Рассмотрим два случая (для двух различных выборов пиксела):

1) Если выбран пиксел E:

2)
Если выбрали пиксел SE, то он имеет координаты (x+1, y-1), а значит, соответствующая ему исрединная точка (x+2, y-3/2). И тогда:

 

 

Таким образом, начиная с самой первой точки (верхняя точка окружности), мы определяем значение d для каждого нового пиксела, и, сравнив его значение с нулем, строим следующий пиксел в дуге окружности.

Рассчитаем значение d в начальной точке дуги (0, R):

Значение d получается вещественным, что требует использования вещественных операций, которых желательно было бы избежать. Сделав замену h=d-1/4, получим, что h=1-R. Тогда необходимо сравнивать h с -1/4, но так как приращения d – целые числа, то сравнение можно заменить сравнением с нулем.

Построение дуги завершим, когда x станет примерно равен у. Вопрос с граничными точками соединения дуг решается отдельно в каждой реализации. Эти точки могут просто дублироваться.