Теоретическое введение. Объектом исследования в данной лабораторной работе является стальная струна, натянутая между двумя точками ее закрепления
Объектом исследования в данной лабораторной работе является стальная струна, натянутая между двумя точками ее закрепления. Составим уравнение колебаний струны. Для простоты рассуждений будем рассматривать малые колебания струны, такие, что ее длину можно считать постоянной.
Найдем вертикальную составляющую силы F, действующей на выделенный элемент струны. Очевидно, что
Так как мы рассматриваем малые колебания,
и тогда
Запишем второй закон Ньютона для элемента струны
где dm – масса элемента струны. Так как
Полученное уравнение можно преобразовать к виду
где Покажем, что полученное уравнение описывает стоячие колебания струны. Для этого его решение запишем в виде
Подстановка этого решения в уравнение /6/ приводит к следующему уравнению
Решение уравнения /8/ ищется в виде
где А, В – постоянные интегрирования. Так как струна закреплена в точках
Из первого условия /10/ следует, что
которое имеет решения при
где Отсюда можно найти
Это уравнение определяет частоты собственных колебаний струны с закрепленными концами. Частота соответствующая
|

 Возьмем малый элемент струны, которому соответствует отрезок
Возьмем малый элемент струны, которому соответствует отрезок 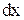 на оси «Х» (рис. 14.1). Мгновенный профиль струны зададим функцией
на оси «Х» (рис. 14.1). Мгновенный профиль струны зададим функцией 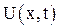 , определяющей отклонение ее элементов от положения равновесия.
, определяющей отклонение ее элементов от положения равновесия. . /1/
. /1/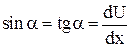 /2/
/2/ . /3/
. /3/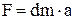 , /4/
, /4/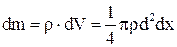 , а
, а 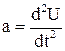 , то
, то . /5/
. /5/ , /6/
, /6/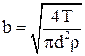 .
. . /7/
. /7/ . /8/
. /8/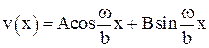 , /9/
, /9/ , то это значит, что
, то это значит, что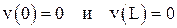 . /10/
. /10/ ; второе условие приводит к соотношению
; второе условие приводит к соотношению , /11/
, /11/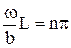 , /12/
, /12/ .
. . /13/
. /13/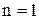 называется основным тоном, а остальные - обертонами.
называется основным тоном, а остальные - обертонами.


