Некоторые сведения о векторах
Определение вектора. Физическая величина, характеризующаяся численным значением и направлением в пространстве, называется вектором. Численное значение вектора называется его модулем. Векторы принято обозначать либо буквами жирного шрифта, например а, либо буквой со стрелкой сверху  . Мы чаще будем использовать именно второй способ.
. Мы чаще будем использовать именно второй способ.
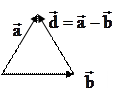
 Сложение и вычитание векторов. Сложение векторов удобно производить с помощью правила параллелограмма. Если на заданных векторах
Сложение и вычитание векторов. Сложение векторов удобно производить с помощью правила параллелограмма. Если на заданных векторах 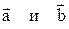 как на сторонах построить параллелограмм, то диагональ его будет равна сумме векторов,
как на сторонах построить параллелограмм, то диагональ его будет равна сумме векторов,  . Разностью двух векторов
. Разностью двух векторов  называется вектор
называется вектор 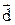 , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  .
.
Умножение вектора на скаляр. В результате умножения вектора  на скаляр
на скаляр  получается новый вектор
получается новый вектор  , модуль которого в
, модуль которого в  раз больше, чем модуль вектора
раз больше, чем модуль вектора  . Направление же вектора
. Направление же вектора  либо совпадает с направлением вектора
либо совпадает с направлением вектора  (если
(если  ), либо противоположно ему (если
), либо противоположно ему (если 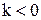 ).
).
 Проекция вектора на ось. Рассмотрим некоторое направление в пространстве, которое мы зададим осью
Проекция вектора на ось. Рассмотрим некоторое направление в пространстве, которое мы зададим осью  . Пусть вектор
. Пусть вектор  образует с нею угол
образует с нею угол  . Величину
. Величину  будем называть проекцией вектора
будем называть проекцией вектора  на ось
на ось  .
.
Проекция вектора на ось есть величина скалярная. Если вектор образует с осью острый угол  , то проекция положительна. Если же угол тупой
, то проекция положительна. Если же угол тупой  , то проекция отрицательна.
, то проекция отрицательна.
 Радиус-вектор. Радиус-вектором
Радиус-вектор. Радиус-вектором  некоторой точки называется вектор, проведенный из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам этой точки:
некоторой точки называется вектор, проведенный из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам этой точки:
 .
.
Следовательно, радиус-вектор можно представить в виде
 ,
,
где 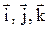 - единичные орты координатных осей.
- единичные орты координатных осей.
Скалярное произведение векторов. Два вектора  можно умножить друг на друга двумя способами, один из которых приводит к скалярной величине, а другой – к векторной. В соответствии с этим существует два произведения векторов – скалярное и векторное.
можно умножить друг на друга двумя способами, один из которых приводит к скалярной величине, а другой – к векторной. В соответствии с этим существует два произведения векторов – скалярное и векторное.
Скалярным произведением векторов  называется скаляр, равный произведению модулей этих векторов на косинус угла
называется скаляр, равный произведению модулей этих векторов на косинус угла  между ними:
между ними:
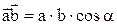 .
.
 При записи скалярного произведения символы перемножаемых векторов пишутся рядом без какого-либо знака между ними. Скалярное произведение двух взаимно перпендикулярных векторов равно нулю. Под квадратом вектора понимается скалярное произведение вектора на самого себя
При записи скалярного произведения символы перемножаемых векторов пишутся рядом без какого-либо знака между ними. Скалярное произведение двух взаимно перпендикулярных векторов равно нулю. Под квадратом вектора понимается скалярное произведение вектора на самого себя  . Таким образом, квадрат вектора равен квадрату его модуля.
. Таким образом, квадрат вектора равен квадрату его модуля.
Векторное произведение векторов. Векторным произведением векторов  называется вектор
называется вектор  , модуль которого определяется выражением
, модуль которого определяется выражением
 ,
,
а направление – правилом правого винта. Направление вектора  совпадает с направлением поступательного перемещения правого винта, если его поворачивать от первого вектора ко второму по кратчайшему пути. Символически векторное произведение записывается двумя способами
совпадает с направлением поступательного перемещения правого винта, если его поворачивать от первого вектора ко второму по кратчайшему пути. Символически векторное произведение записывается двумя способами
 .
.
Векторы, направления которых связывается с направлением вращения, называются псевдовекторами или осевыми векторами.
Поскольку направление векторного произведения определяется направлением вращения от первого сомножителя ко второму, то результат векторного умножения зависит от порядка сомножителей. Перестановка сомножителей вызывает изменение направления результирующего вектора на противоположное, т.е.
 .
.

 . Мы чаще будем использовать именно второй способ.
. Мы чаще будем использовать именно второй способ.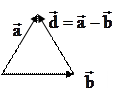
 Сложение и вычитание векторов. Сложение векторов удобно производить с помощью правила параллелограмма. Если на заданных векторах
Сложение и вычитание векторов. Сложение векторов удобно производить с помощью правила параллелограмма. Если на заданных векторах 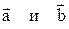 как на сторонах построить параллелограмм, то диагональ его будет равна сумме векторов,
как на сторонах построить параллелограмм, то диагональ его будет равна сумме векторов,  . Разностью двух векторов
. Разностью двух векторов  называется вектор
называется вектор 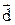 , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  получается новый вектор
получается новый вектор  , модуль которого в
, модуль которого в  ), либо противоположно ему (если
), либо противоположно ему (если 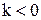 ).
). Проекция вектора на ось. Рассмотрим некоторое направление в пространстве, которое мы зададим осью
Проекция вектора на ось. Рассмотрим некоторое направление в пространстве, которое мы зададим осью  . Пусть вектор
. Пусть вектор  . Величину
. Величину  будем называть проекцией вектора
будем называть проекцией вектора  .
. , то проекция положительна. Если же угол тупой
, то проекция положительна. Если же угол тупой  , то проекция отрицательна.
, то проекция отрицательна. Радиус-вектор. Радиус-вектором
Радиус-вектор. Радиус-вектором  некоторой точки называется вектор, проведенный из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам этой точки:
некоторой точки называется вектор, проведенный из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам этой точки: .
. ,
,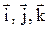 - единичные орты координатных осей.
- единичные орты координатных осей. между ними:
между ними: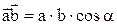 .
. При записи скалярного произведения символы перемножаемых векторов пишутся рядом без какого-либо знака между ними. Скалярное произведение двух взаимно перпендикулярных векторов равно нулю. Под квадратом вектора понимается скалярное произведение вектора на самого себя
При записи скалярного произведения символы перемножаемых векторов пишутся рядом без какого-либо знака между ними. Скалярное произведение двух взаимно перпендикулярных векторов равно нулю. Под квадратом вектора понимается скалярное произведение вектора на самого себя  . Таким образом, квадрат вектора равен квадрату его модуля.
. Таким образом, квадрат вектора равен квадрату его модуля. , модуль которого определяется выражением
, модуль которого определяется выражением ,
, .
. .
.


