Регрессионный анализ
Из курса лекций вы знаете, что наличие корреляции дает возможность делать прогнозы с помощью процедуры, называемой «регрессионным анализом». Линия регрессии служит основой для построения прогноза. На основе рассчитанного выше пирсонова r, определите каков предположительный балл на экзамене получит студент, который потратил без пользы 15 часов занятий по предмету. Формула для нахождения линейной регрессии и образец расчета приведены ниже. Y=a+bХ а –точка на оси Y b – наклон кривой Х – известное значение Y –предполагаемое значение Вычислим все составляющие: b=r r- пирсоново r =- 0.89;
Sy – стандартное отклонение = 0.63 b=-0.89 _ _ a= Y- bX _ где Y среднее арифметическое для Y= 2.8 _ Х среднее арифметическое для Х= 28. 88 а=2.8- (-0.06)(28.88)=4.53 Подставим значение для точки на оси Y и наклона кривой в формулу регрессии: Y= a+bХ =4.53+(-0.06)Х= 4.53-0.06 Х Используем формулу для расчета предположения: Если студент потратил без пользы 40 часов занятий по предмету, то его предположительный балл на экзамене равен: Y= a+bХ=4.53-0.06 × 40 = 2.13
Домашнее задание. Используя лекционный материал, ответьте на следующие вопросы: 1. Какие гипотезы проверяются в корреляционных исследованиях? 2. Почему корреляционные исследования относятся к «пассивно-наблюдающим»? 3. Чем корреляционные исследования отличаются от истинного эксперимента? 4. Какие способы представления результатов используются в корреляционном исследовании.
|
– стандартное отклонение = 9.43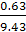
= -0.06
