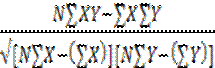График рассеивания, вычисление Пирсонова r и регрессии

Пользуясь материалами лекций, ответьте на следующие вопросы:

1. Что такое график рассеивания и какой вид он может принимать?

2. Что такое регрессия?

По приведенным ниже данным постройте график рассеяния. На основании графика предположите, какой должна быть корреляция, а затем с помощью процедуры, описанной ниже, вычислите действительное значение пирсонова r. Затем найдите коэффициент детерминации и опишите обнаруженную взаимосвязь. В заключение подставьте полученные данные в уравнение регрессии и сделайте предположение о «манере объяснять» Эда (его значение самооценки равно 10), Неда (самооценка равна 20) и Фреда (самооценка равна 30).

1. Переменная А = самооценка: оценки варьируются от 0 до 50; более высокие оценки говорят о более высокой самооценке.

2. Переменная В = «манера объяснять»: оценки варьируются от 0 до 75; более высокие оценки говорят об отрицательном, или пессимистичном, способе интерпретации жизненных сложностей, а более низкие оценки — о положи­тельном, или оптимистичном, способе объяснения тех же событий.

Таблица 11

Результаты исследования самооценки и манеры объяснять жизненные события

N испытуемого ПеременнаяА Переменная В

 

 

Алгоритм расчета пирсонова r

Если обе переменные измеряются либо по интервальной шкале, либо по шкале отношений, их взаимосвязь можно оценить с помощью пирсонова г. Предположим, к примеру, что исследователь хочет определить взаимосвязь между количеством времени, бесполезно потраченного студентами, и их средним баллом. Средний балл варьируется от 0, 0 до 4, 0, а потраченное без пользы время — это количество часов, проводимых в неделю за определенными занятиями (например, просмотром мыль­ных опер). Для восьми студентов получены следующие данные

Таблица 12

Количество времени потраченного без пользы и средний балл учебной успешности

№	Бесполезно потраченное время переменная Х	Х2	Средний балл переменная У	У2	Х× У
			1.8	3.24	75.6
			3.0	9.0	69.0
			2.2	4.84	68.2
			2.9	8.41	101.5
			3.7	13.69	59.2
			3.0	9.0	78.0
			2.4	5.76	93.6
			3.4	11.56	64.5
сумма			22.4	65.5	609.7

 

Формула вычисления Пирсонова r:

R=
Вычислите все составляющие

N∑ XY=(8)(609.7)=4877.6

∑ X∑ Y=(231)(22.4)=5174.4

N∑ X =(8)(7263)=58344

(∑ X) =(231)(231)=53361

N∑ Y =(8)(65.5)=524

∑ (∑ Y) =(22.4)(22.4)=501.76

Подставим значение в формулу и вычислим ее значение.

R=

R=-0.89

Определим, является ли полученное значение значимым, то есть отличается ли от нуля. Это можно узнать с помощью таблицы критических значений. Сначала определим степень свободы. Число степеней свободы для Пирсонова r =n-2, где n –количество пар оценок. В данном случае 8-2=6. В таблице необходимо определить два критических значения: для уровня значимости 0.05 значение равно 0.707; и для уровня 0.01 значение критерия равно 0.834.

Вывод: если найденное значение равняется или превышает критическое значение, то можно отвергнуть нулевую гипотезу. Корреляция является статистически значимой на 0.01 уровне, так как значение – 0, 89 больше критического значения, равного 0.834. Знак корреляции не важен, важно его абсолютное значение.