Определение предела функции
Рассмотрим теперь действительную функцию  действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть
действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть 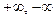 или просто
или просто 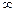 ).
).
Определение 8. 1) Предположим, что существует хотя бы одна последовательность 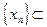 D(y), строго стремящаяся к a. Точка b называется пределом функции
D(y), строго стремящаяся к a. Точка b называется пределом функции  при x стремящемся к a, если для любой последовательности
при x стремящемся к a, если для любой последовательности 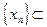 D(y), строго стремящейся к a, выполняется соотношение:
D(y), строго стремящейся к a, выполняется соотношение: 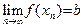 . Тот факт, что b является пределом функции
. Тот факт, что b является пределом функции  при х стремящемся к a, обозначают так:
при х стремящемся к a, обозначают так:  .
.
2) Предположим, что существует хотя бы одна последовательность 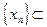 D(y), строго монотонно возрастающая (соответственно, строго монотонно убывающая) к a. Точка b называется левым (соответственно правым) пределом функции
D(y), строго монотонно возрастающая (соответственно, строго монотонно убывающая) к a. Точка b называется левым (соответственно правым) пределом функции  при x стремящемся к a, если для любой последовательности
при x стремящемся к a, если для любой последовательности 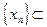 D(y), строго монотонно возрастающей (соответственно, строго монотонно убывающей) к a, выполняется соотношение:
D(y), строго монотонно возрастающей (соответственно, строго монотонно убывающей) к a, выполняется соотношение: 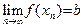 . Обозначение левого предела:
. Обозначение левого предела: 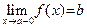 (соответственно, правого предела:
(соответственно, правого предела:  ). Ÿ
). Ÿ
Отметим, что из определения 8 сразу вытекает, что если предел (левый предел, правый предел) функции существует, то этот предел единственен.
Пример 4. Рассмотрим функцию
|
|  . .
|
|
Ее график имеет вид:
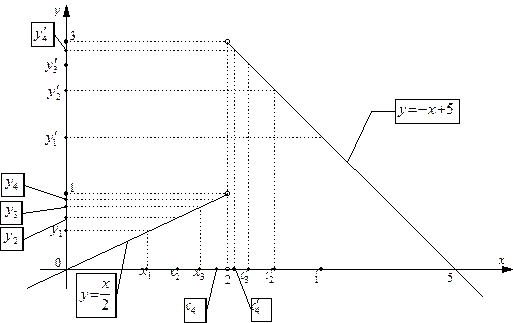
Заметим, что данная функция не определена в точке 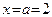 . Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность
. Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность  , фигурирующая в определении 8, не посещает предельную точку
, фигурирующая в определении 8, не посещает предельную точку  .
.
Рассмотрим сначала последовательность  , строго монотонно возрастающую к
, строго монотонно возрастающую к  , и обозначим
, и обозначим 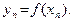 Так как
Так как 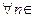 N
N  , то, используя вид нашей функции, получаем:
, то, используя вид нашей функции, получаем:  . Из рисунка видно, что при
. Из рисунка видно, что при 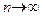 последовательность
последовательность  . Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):
. Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):  . Это означает, что
. Это означает, что  .
.
Рассмотрим теперь последовательность 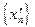 , строго монотонно убывающую к
, строго монотонно убывающую к  , и обозначим
, и обозначим 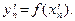 Так как
Так как 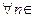 N
N  , то, используя вид нашей функции, получаем:
, то, используя вид нашей функции, получаем:  . Опять из рисунка видно, что при
. Опять из рисунка видно, что при 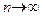 последовательность
последовательность 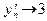 . Это же можно вычислить аналитически:
. Это же можно вычислить аналитически:  . Это означает, что
. Это означает, что  .
.
Ясно, что 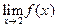 не существует. Действительно, рассмотрим последовательность
не существует. Действительно, рассмотрим последовательность  , которая, очевидно, строго стремится к точке
, которая, очевидно, строго стремится к точке  . Однако для последовательности соответствующих значений функции
. Однако для последовательности соответствующих значений функции  , то есть для последовательности
, то есть для последовательности  , получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что
, получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что 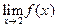 не существует. Читателю предлагается скрупулезно произвести все необходимые рассуждения.
не существует. Читателю предлагается скрупулезно произвести все необходимые рассуждения.
Пример 5. Переместим параллельно самой себе правую ветвь графика из примера 4 на 2 единицы вниз. Получим следующий график:

Это график функции:
|
|  . .
|
|
Рассуждая так же, как в примере 4, легко получить, что  ,
,  , и предел функции при
, и предел функции при  существует и равен 1, то есть
существует и равен 1, то есть  .
.
Примеры 4 и 5 побуждают нас сформулировать следующую теорему, доказательство которой мы опускаем.
Теорема 2. Если  , то
, то  .
.
Читателю предлагается подумать, как можно сформулировать обратную теорему.
Пример 6. Рассмотрим функцию  , где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)=
, где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)= 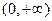 . Рассмотрим точку
. Рассмотрим точку  . Очевидно, что не существует последовательности
. Очевидно, что не существует последовательности 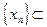 D(y), стремящейся к
D(y), стремящейся к  . Поэтому бессмысленно говорить о пределе функции
. Поэтому бессмысленно говорить о пределе функции  при
при  (именно поэтому в определении 8 требуется существование хотя бы одной последовательности
(именно поэтому в определении 8 требуется существование хотя бы одной последовательности 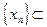 D(y), строго стремящейся к предельной точке a).
D(y), строго стремящейся к предельной точке a).
Пусть теперь  . Ясно, что не существует последовательности
. Ясно, что не существует последовательности 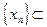 D(y), строго монотонно возрастающей к
D(y), строго монотонно возрастающей к  (то есть о левом пределе говорить бессмысленно). Однако существуют последовательности
(то есть о левом пределе говорить бессмысленно). Однако существуют последовательности 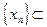 D(y), строго монотонно убывающие к
D(y), строго монотонно убывающие к  (например, можно взять
(например, можно взять  ). Легко видеть (постройте график!), что для таких последовательностей
). Легко видеть (постройте график!), что для таких последовательностей  . Это означает, что
. Это означает, что  . Вместе с этим и
. Вместе с этим и 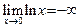 .
.
Свойства предела функции
Во всех нижеперечисленных свойствах, если речь идет о двух функциях  и
и  , то предполагается, что существует последовательность
, то предполагается, что существует последовательность 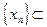 D(f)Ç D(g), строго стремящаяся к a.
D(f)Ç D(g), строго стремящаяся к a.
1. Предел константы равен самой этой константе, то есть если 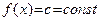 то
то
|
|  . .
|
|
2. Предел суммы двух функций равен сумме пределов этих функций, то есть если 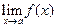 и
и  существуют и конечны, то
существуют и конечны, то
3. Постоянный множитель можно вынести за знак предела, то есть если 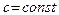 и
и 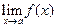 существует и конечен, то
существует и конечен, то
|
|   . .
|
|
4. Предел произведения двух функций равен произведению пределов этих функций, то есть если 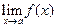 и
и  существуют и конечны, то
существуют и конечны, то
|
|  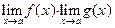 . .
|
|
5. Предел частного двух функций равен частному пределов этих функций, то есть если 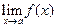 и
и  существуют, конечны и
существуют, конечны и  , то
, то
|
|  . .
|
|
6. Если в некоторой окрестности точки a (исключая, быть может, саму точку a) 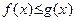 и пределы
и пределы 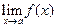 и
и  существуют, то
существуют, то
|
| 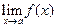 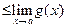 . .
|
|
7. Если 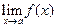 =
=  = b и если в некоторой окрестности точки a (исключая, быть может, саму точку a)
= b и если в некоторой окрестности точки a (исключая, быть может, саму точку a)  то предел функции
то предел функции  существует и
существует и
|
|  . .
|
|
8. Если в некоторой окрестности точки a (исключая, быть может, саму точку a) функция  ограничена (то есть
ограничена (то есть  , такое, что в этой окрестности
, такое, что в этой окрестности  ), а
), а  , то
, то
|
| 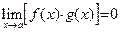 . .
|
|
Доказательства всех этих свойств немедленно следуют из определения 8 и соответствующих свойств предела последовательности.
Замечательные пределы
1.  (первый замечательный предел).
(первый замечательный предел).
Доказательство. Прежде всего покажем, что при  выполняется неравенство:
выполняется неравенство:
|
| 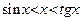
| (4)
|
Обозначим площадь сектора AOB построенного единичного круга через S. Тогда  . Имеем:
. Имеем:  ,
,  ,
, 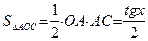 . Отсюда получаем выполнение (4). Поделив неравенство (4) на
. Отсюда получаем выполнение (4). Поделив неравенство (4) на  , получим:
, получим: 
 . Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство:
. Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство: 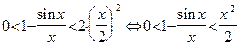 . В силу четности функций
. В силу четности функций 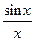 и
и 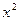 последнее двойное неравенство справедливо не только при
последнее двойное неравенство справедливо не только при  , но и при
, но и при  . Так как
. Так как  , то по свойству 7 предела функции имеем:
, то по свойству 7 предела функции имеем:  , откуда немедленно следует равенство
, откуда немедленно следует равенство  . œ
. œ
2.  (второй замечательный предел).
(второй замечательный предел).
Доказательство опускается (см. пример 3 и определение 6). œ

 действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть
действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть 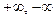 или просто
или просто 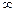 ).
).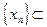 D(y), строго стремящаяся к a. Точка b называется пределом функции
D(y), строго стремящаяся к a. Точка b называется пределом функции 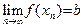 . Тот факт, что b является пределом функции
. Тот факт, что b является пределом функции  .
.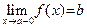 (соответственно, правого предела:
(соответственно, правого предела:  ). Ÿ
). Ÿ .
.
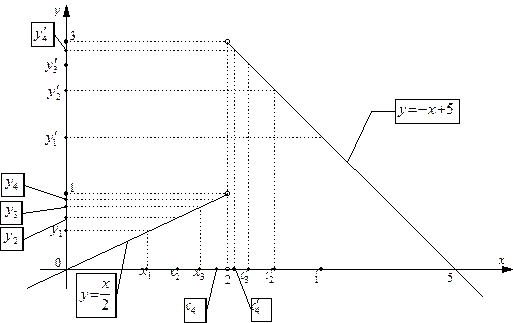
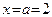 . Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность
. Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность  , фигурирующая в определении 8, не посещает предельную точку
, фигурирующая в определении 8, не посещает предельную точку  .
.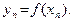 Так как
Так как 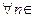 N
N  , то, используя вид нашей функции, получаем:
, то, используя вид нашей функции, получаем:  . Из рисунка видно, что при
. Из рисунка видно, что при 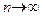 последовательность
последовательность  . Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):
. Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):  . Это означает, что
. Это означает, что  .
.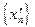 , строго монотонно убывающую к
, строго монотонно убывающую к 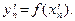 Так как
Так как  , то, используя вид нашей функции, получаем:
, то, используя вид нашей функции, получаем:  . Опять из рисунка видно, что при
. Опять из рисунка видно, что при 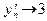 . Это же можно вычислить аналитически:
. Это же можно вычислить аналитически:  . Это означает, что
. Это означает, что  .
.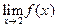 не существует. Действительно, рассмотрим последовательность
не существует. Действительно, рассмотрим последовательность  , которая, очевидно, строго стремится к точке
, которая, очевидно, строго стремится к точке  , получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что
, получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что 
 .
.
 , и предел функции при
, и предел функции при  существует и равен 1, то есть
существует и равен 1, то есть  .
. , то
, то  , где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)=
, где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)= 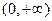 . Рассмотрим точку
. Рассмотрим точку  . Очевидно, что не существует последовательности
. Очевидно, что не существует последовательности  при
при  (именно поэтому в определении 8 требуется существование хотя бы одной последовательности
(именно поэтому в определении 8 требуется существование хотя бы одной последовательности  . Ясно, что не существует последовательности
. Ясно, что не существует последовательности  (то есть о левом пределе говорить бессмысленно). Однако существуют последовательности
(то есть о левом пределе говорить бессмысленно). Однако существуют последовательности  ). Легко видеть (постройте график!), что для таких последовательностей
). Легко видеть (постройте график!), что для таких последовательностей  . Это означает, что
. Это означает, что  . Вместе с этим и
. Вместе с этим и 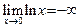 .
. , то предполагается, что существует последовательность
, то предполагается, что существует последовательность 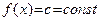 то
то .
.
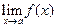 и
и  существуют и конечны, то
существуют и конечны, то =
= 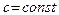 и
и 
 .
.

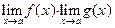 .
.
 существуют, конечны и
существуют, конечны и  , то
, то .
.
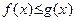 и пределы
и пределы 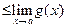 .
.
 то предел функции
то предел функции  существует и
существует и .
.
 , такое, что в этой окрестности
, такое, что в этой окрестности  ), а
), а  , то
, то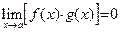 .
.
 (первый замечательный предел).
(первый замечательный предел). выполняется неравенство:
выполняется неравенство: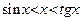

 . Имеем:
. Имеем:  ,
,  ,
, 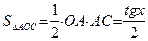 . Отсюда получаем выполнение (4). Поделив неравенство (4) на
. Отсюда получаем выполнение (4). Поделив неравенство (4) на  , получим:
, получим: 
 . Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство:
. Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство: 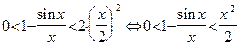 . В силу четности функций
. В силу четности функций 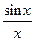 и
и 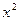 последнее двойное неравенство справедливо не только при
последнее двойное неравенство справедливо не только при  . Так как
. Так как  , то по свойству 7 предела функции имеем:
, то по свойству 7 предела функции имеем:  , откуда немедленно следует равенство
, откуда немедленно следует равенство  (второй замечательный предел).
(второй замечательный предел).


